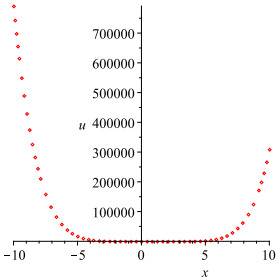
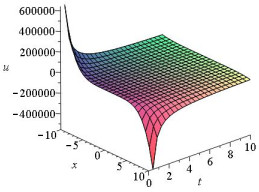
|
[1]
|
E. A. B. Abdel Salam and G. F. Hassan, Multiwave solutions of fractional 4th and 5th order Burgers equations., Tur. J. Phys., 2015, 39(3), 227-241.
Google Scholar
|
|
[2]
|
A. Abourabia, K. Hassan and E. Selima, Painlevé analysis and new analytical solutions for compound KdV-Burgers equation with variable coefficients, Can. J. Phys., 2010, 88(3), 211-221. doi: 10.1139/P10-003
CrossRef Google Scholar
|
|
[3]
|
A. Abourabia and A. Morad, Exact traveling wave solutions of the van der Waals normal form for fluidized granular matter, Physica A, 2015, 437, 333-350. doi: 10.1016/j.physa.2015.06.005
CrossRef Google Scholar
|
|
[4]
|
S. C. Anco and G. Bluman, Direct construction method for conservation laws of partial differential equations Part Ⅰ: Examples of conservation law classifications, Eur. J. Appl. Math., 2002, 13(5), 545-566. doi: 10.1017/S095679250100465X
CrossRef Google Scholar
|
|
[5]
|
T. M. Atanacković, S. Konjik, S. Pilipović and S. Simić, Variational problems with fractional derivatives: Invariance conditions and Noether's theorem, Nonlinear Anal., 2009, 71(5), 1504-1517.
Google Scholar
|
|
[6]
|
A. Bekir, Ö. Güner and A. C. Cevikel, Fractional complex transform and expfunction methods for fractional differential equations, Abstr. Appl. Anal., 2013, 2013.
Google Scholar
|
|
[7]
|
A. Bekir, Ö. Güner and Ö. Unsal, The first integral method for exact solutions of nonlinear fractional differential equations, J. Comput. Nonlinear Dyn., 2015, 10(2), 021020. doi: 10.1115/1.4028065
CrossRef Google Scholar
|
|
[8]
|
Z. Bin, G'/G-expansion method for solving fractional partial differential equations in the theory of mathematical physics, Commun. Theor. Phys., 2012, 58(5), 623. doi: 10.1088/0253-6102/58/5/02
CrossRef Google Scholar
|
|
[9]
|
A. Biswas, Solitary wave solution for the generalized KdV equation with timedependent damping and dispersion, Commun. Nonlinear Sci. Numer. Simul., 2009, 14(9-10), 3503-3506. doi: 10.1016/j.cnsns.2008.09.026
CrossRef Google Scholar
|
|
[10]
|
G. W. Bluman and J. D. Cole, Similarity methods for differential equations, Springer-Verlag, Berlin, 1974.
Google Scholar
|
|
[11]
|
G. W. Bluman and S. Kumei, Symmetries and differential equations, SpringerVerlag, New York, 1989.
Google Scholar
|
|
[12]
|
L. Bourdin, J. Cresson and I. Greff, A continuous/discrete fractional Noethers theorem, Commun. Nonlinear Sci. Numer. Simul., 2013, 18(4), 878-887. doi: 10.1016/j.cnsns.2012.09.003
CrossRef Google Scholar
|
|
[13]
|
I. Colombaro, A. Giusti and F. Mainardi, Wave dispersion in the linearised fractional Korteweg-de Vries equation, arXiv preprint arXiv: 1704.02508, 2017.
Google Scholar
|
|
[14]
|
A. Fokas and L. Luo, On the asymptotic integrability of a generalized Burgers equation, Contemp. Math., 1996, 200, 85-98.
Google Scholar
|
|
[15]
|
G. S. F. Frederico and D. F. M. Torres, A formulation of Noether's theorem for fractional problems of the calculus of variations, J. Math. Anal. Appl., 2007, 334(2), 834-846. doi: 10.1016/j.jmaa.2007.01.013
CrossRef Google Scholar
|
|
[16]
|
V. A. Galaktionov and S. R. Svirshchevskii, Exact solutions and invariant subspaces of nonlinear partial differential equations in mechanics and physics, CRC Press, 2006.
Google Scholar
|
|
[17]
|
R. K. Gazizov, N. H. Ibragimov and S. Y. Lukashchuk, Nonlinear selfadjointness, conservation laws and exact solutions of time-fractional Kompaneets equations, Commun. Nonlinear Sci. Numer. Simul., 2015, 23(1), 153-163.
Google Scholar
|
|
[18]
|
R. K. Gazizov, A. A. Kasatkin and S. Y. Lukashchuk, Continuous transformation groups of fractional differential equations, USATU, 2007, 9(3), 21.
Google Scholar
|
|
[19]
|
R. K. Gazizov, A. A. Kasatkin and S. Y. Lukashchuk, Symmetry properties of fractional diffusion equations, Phys. Scr., 2009, 2009(T136), 014016.
Google Scholar
|
|
[20]
|
V. Gerdjikov, G. Vilasi and A. B. Yanovski, Integrable hamiltonian hierarchies, Springer, Berlin, 2008.
Google Scholar
|
|
[21]
|
A. Giusti, Dispersion relations for the time-fractional Cattaneo-Maxwell heat equation, J. Math. Phys., 2018, 59(1), 013506. doi: 10.1063/1.5001555
CrossRef Google Scholar
|
|
[22]
|
M. S. Hashemi, Group analysis and exact solutions of the time fractional Fokker-Planck equation, Physica A, 2015, 417, 141-149. doi: 10.1016/j.physa.2014.09.043
CrossRef Google Scholar
|
|
[23]
|
Q. Huang and R. Zhdanov, Symmetries and exact solutions of the time fractional Harry-Dym equation with Riemann-Liouville derivative, Physica A, 2014, 409, 110-118. doi: 10.1016/j.physa.2014.04.043
CrossRef Google Scholar
|
|
[24]
|
N. H. Ibragimov, A new conservation theorem, J. Math. Anal. Appl., 2007, 333(1), 311-328. doi: 10.1016/j.jmaa.2006.10.078
CrossRef Google Scholar
|
|
[25]
|
M. Inc, A. Yusuf, A. I. Aliyu et al., Lie symmetry analysis and explicit solutions for the time fractional generalized Burgers-Huxley equation, Opt. Quantum.Electron., 2018, 50(2), 94. doi: 10.1007/s11082-018-1373-8
CrossRef Google Scholar
|
|
[26]
|
M. Inc, A. Yusuf, A. I. Aliyu et al., Lie symmetry analysis, explicit solutions and conservation laws for the space-time fractional nonlinear evolution equations, Physica A, 2018, 496, 371-383. doi: 10.1016/j.physa.2017.12.119
CrossRef Google Scholar
|
|
[27]
|
M. Inc, A. Yusuf, A. I. Aliyu et al., Time-fractional cahn-allen and timefractional Klein-Gordon equations: lie symmetry analysis, explicit solutions and convergence analysis, Physica A, 2018, 493, 94-106. doi: 10.1016/j.physa.2017.10.010
CrossRef Google Scholar
|
|
[28]
|
H. Jafari, N. Kadkhoda and D. Baleanu, Fractional Lie group method of the time-fractional Boussinesq equation, Nonlinear Dyn., 2015, 81(3), 1569-1574. doi: 10.1007/s11071-015-2091-4
CrossRef Google Scholar
|
|
[29]
|
G. F. Jefferson and J. Carminati, FracSym: Automated symbolic computation of Lie symmetries of fractional differential equations, Comput. Phys. Commun., 2014, 185(1), 430-441. doi: 10.1016/j.cpc.2013.09.019
CrossRef Google Scholar
|
|
[30]
|
A. H. Kara and F. M. Mahomed, Noether-type symmetries and conservation laws via partial Lagrangians, Nonlinear Dyn., 2006, 45(3), 367-383.
Google Scholar
|
|
[31]
|
B. Kaur and R. K. Gupta, Invariance properties, conservation laws, and soliton solutions of the time-fractional (2+1)-dimensional new coupled ZK system in magnetized dusty plasmas, Comput. Appl. Math., 2018, 37(5), 5981-6004. doi: 10.1007/s40314-018-0674-7
CrossRef Google Scholar
|
|
[32]
|
B. Kaur and R. K. Gupta, Dispersion analysis and improved F-expansion method for space-time fractional differential equations, Nonlinear Dyn., 2019, 96(2), 837-852. doi: 10.1007/s11071-019-04825-w
CrossRef Google Scholar
|
|
[33]
|
B. Kaur and R. K. Gupta, Multiple types of exact solutions and conservation laws of new coupled (2+1)-dimensional Zakharov-Kuznetsov system with timedependent coefficients, Pramana −J. Phys., 2019, 93(4), 59. doi: 10.1007/s12043-019-1806-3
CrossRef Google Scholar
|
|
[34]
|
B. Kaur and R. K. Gupta, Time fractional (2+1)-dimensional Wu-Zhang system: Dispersion analysis, similarity reductions, conservation laws, and exact solutions, Comput. Math. Appl., 2020, 79(4), 1031-1048. doi: 10.1016/j.camwa.2019.08.014
CrossRef Google Scholar
|
|
[35]
|
T. Kawahara, Formation of saturated solitons in a nonlinear dispersive system with instability and dissipation, Phys. Rev. Lett., 1983, 51(5), 381. doi: 10.1103/PhysRevLett.51.381
CrossRef Google Scholar
|
|
[36]
|
A. Kilbas, H. Srivastava and J. Trujillo, Theory and applications of fractional differential equations, Elsevier, Boston, 2006.
Google Scholar
|
|
[37]
|
V. S. Kiryakova, Generalized fractional calculus and applications, Pitman Research Notes in Mathematics Series (Longman Scientific & Technical, Longman Group, UK), 1994.
Google Scholar
|
|
[38]
|
R. A. Kraenkel, J. Pereira and E. de Rey Neto, Linearizability of the perturbed burgers equation, Phys. Rev. E, 1998, 58(2), 2526. doi: 10.1103/PhysRevE.58.2526
CrossRef Google Scholar
|
|
[39]
|
N. A. Kudryashov and D. I. Sinelshchikov, Extended models of non-linear waves in liquid with gas bubbles, Int. J. Non Linear Mech., 2014, 63, 31-38. doi: 10.1016/j.ijnonlinmec.2014.03.011
CrossRef Google Scholar
|
|
[40]
|
S. Y. Lukashchuk, Conservation laws for time-fractional subdiffusion and diffusion-wave equations, Nonlinear Dyn., 2015, 80(1-2), 791-802. doi: 10.1007/s11071-015-1906-7
CrossRef Google Scholar
|
|
[41]
|
F. Mainardi, On signal velocity for anomalous dispersive waves, Il Nuovo Cimento B (1971-1996), 1983, 74(1), 52-58. doi: 10.1007/BF02721684
CrossRef Google Scholar
|
|
[42]
|
F. Mainardi, Fractional calculus and waves in linear viscoelasticity: an introduction to mathematical models, World Scientific, London-Singapore, 2010.
Google Scholar
|
|
[43]
|
A. B. Malinowska, A formulation of the fractional Noether-type theorem for multidimensional Lagrangians, Appl. Math. Lett., 2012, 25(11), 1941-1946. doi: 10.1016/j.aml.2012.03.006
CrossRef Google Scholar
|
|
[44]
|
K. S. Miller and B. Ross, An introduction to the fractional calculus and fractional differential equations, Wiley-Interscience, 1993.
Google Scholar
|
|
[45]
|
E. Noether, Invariante variationsprobleme, Nachr. d. König. Gesellsch. d. Wiss.zu Göttingen, Math-phys. Klasse, 1918, 1(3), 235-257.
Google Scholar
|
|
[46]
|
T. Odzijewicz, A. Malinowska and D. Torres, Noethers theorem for fractional variational problems of variable order, Cent. Eur. J. Phys., 2013, 11(6), 691-701.
Google Scholar
|
|
[47]
|
K. B. Oldham and J. Spanier, The Fractional Calculus, vol. 111 of Mathematics in science and engineering, Academic Press, New York, London, 1974.
Google Scholar
|
|
[48]
|
P. J. Olver, Applications of Lie groups to differential equations, 107, Graduate Texts in Mathematics. Springer-Verlag, Berlin, 1993.
Google Scholar
|
|
[49]
|
I. Podlubny, Fractional Differential Equations, Academic press, 1999.
Google Scholar
|
|
[50]
|
P. Prakash and R. Sahadevan, Lie symmetry analysis and exact solution of certain fractional ordinary differential equations, Nonlinear Dyn., 2017, 89(1), 305-319. doi: 10.1007/s11071-017-3455-8
CrossRef Google Scholar
|
|
[51]
|
C. Qin, S. Tian, X. Wang and T. Zhang, Lie symmetries, conservation laws and explicit solutions for time fractional Rosenau-Haynam equation, Commun. Theor. Phys., 2017, 67(2), 157. doi: 10.1088/0253-6102/67/2/157
CrossRef Google Scholar
|
|
[52]
|
W. Rudin, Principles of Mathematical Analysis, China Machine Press, Beijing, 2004.
Google Scholar
|
|
[53]
|
W. Rui and X. Zhang, Lie symmetries and conservation laws for the time fractional Derrida-Lebowitz-Speer-Spohn equation, Commun. Nonlinear Sci. Numer. Simul., 2016, 34, 38-44. doi: 10.1016/j.cnsns.2015.10.004
CrossRef Google Scholar
|
|
[54]
|
R. Sahadevan and T. Bakkyaraj, Invariant analysis of time fractional generalized Burgers and Korteweg-de Vries equations, J. Math. Anal. Appl., 2012, 393(2), 341-347. doi: 10.1016/j.jmaa.2012.04.006
CrossRef Google Scholar
|
|
[55]
|
S. G. Samko, A. A. Kilbas, O. I. Marichev et al., Fractional integrals and derivatives, 1993, Theory and Applications, Gordon and Breach, Yverdon, 1993.
Google Scholar
|
|
[56]
|
K. Singla and R. Gupta, On invariant analysis of space-time fractional nonlinear systems of partial differential equations. ii, J. Math. Phys., 2017, 58(5), 051503. doi: 10.1063/1.4982804
CrossRef Google Scholar
|
|
[57]
|
K. Singla and R. K. Gupta, On invariant analysis of some time fractional nonlinear systems of partial differential equations. I, J. Math. Phys., 2016, 57(10), 101504. doi: 10.1063/1.4964937
CrossRef Google Scholar
|
|
[58]
|
K. Singla and R. K. Gupta, Generalized Lie symmetry approach for fractional order systems of differential equations. Ⅲ, J. Math. Phys., 2017, 58(6), 061501. doi: 10.1063/1.4984307
CrossRef Google Scholar
|
|
[59]
|
G. Wang, A. H. Kara and K. Fakhar, Symmetry analysis and conservation laws for the class of time-fractional nonlinear dispersive equation, Nonlinear Dyn., 2015, 82(1-2), 281-287. doi: 10.1007/s11071-015-2156-4
CrossRef Google Scholar
|
|
[60]
|
G. Wang and T. Xu, Invariant analysis and exact solutions of nonlinear time fractional Sharma-Tasso-Olver equation by Lie group analysis, Nonlinear Dyn., 2014, 76(1), 571-580. doi: 10.1007/s11071-013-1150-y
CrossRef Google Scholar
|
|
[61]
|
A. M. Wazwaz, Partial differential equations and solitary waves theory, 2009.
Google Scholar
|
|
[62]
|
A. M. Wazwaz, Burgers hierarchy: Multiple kink solutions and multiple singular kink solutions, J. Franklin Inst., 2010, 347(3), 618-626. doi: 10.1016/j.jfranklin.2010.01.003
CrossRef Google Scholar
|
|
[63]
|
G. Whitham, Linear and Nonlinear Waves, John Wiley and Sons, New York(1974), Wiley, New York, 1974.
Google Scholar
|
|
[64]
|
E. Yaşsar, Y. Yıldırım and C. M. Khalique, Lie symmetry analysis, conservation laws and exact solutions of the seventh-order time fractional Sawada-Kotera- Ito equation, Results Phys., 2016, 6, 322-328. doi: 10.1016/j.rinp.2016.06.003
CrossRef Google Scholar
|
|
[65]
|
F. You and T. Xia, The integrable couplings of the generalized coupled Burgers hierarchy and its Hamiltonian structures, Chaos Solitons Fractals, 2008, 36(4), 953-960. doi: 10.1016/j.chaos.2006.07.029
CrossRef Google Scholar
|
|
[66]
|
S. Zhang and H. Zhang, Fractional sub-equation method and its applications to nonlinear fractional PDEs, Phys. Lett. A, 2011, 375(7), 1069-1073. doi: 10.1016/j.physleta.2011.01.029
CrossRef Google Scholar
|




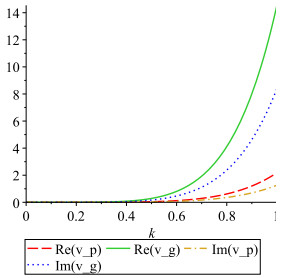

 DownLoad:
DownLoad: