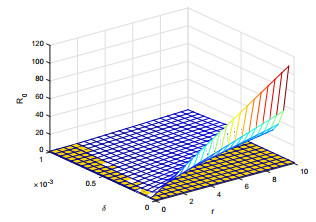
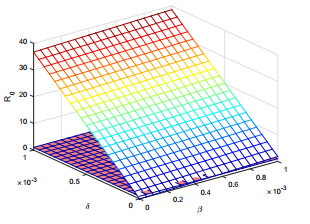
|
[1]
|
C. N. Angstmann, B. I. Henry and A. V. McGann, A fractional order recovery SIR model from a stochastic process, Bulletin of Mathematical Biology, 2016, 78(3), 468-499. doi: 10.1007/s11538-016-0151-7
CrossRef Google Scholar
|
|
[2]
|
Y. Bai and X. Mu, Global asymptotic stability of a generalized SIRS epidemic model with transfer from infectious to susceptible, Journal of Applied Analysis & Computation, 2018, 8(2), 402-412.
Google Scholar
|
|
[3]
|
M. Bani-Yaghoub, R. Gautam, Z. Shuai et al., Reproduction numbers for infections with free-living pathogens growing in the environment, Journal of Biological Dynamics, 2012, 6(2), 923-940. doi: 10.1080/17513758.2012.693206
CrossRef Google Scholar
|
|
[4]
|
D. Bichara, Y. Kang, C. Castillo-Chavez et al., SIS and SIR epidemic models under virtual dispersal, Bulletin of Mathematical Biology, 2015, 77(11), 2004-2034. doi: 10.1007/s11538-015-0113-5
CrossRef Google Scholar
|
|
[5]
|
D. J. Bolton, C. M. Byrne, J. J. Sheridan et al., The survival characteristics of a non-toxigenic strain of escherichia coli O157:H7, Journal of Applied Microbiology, 1999, 86(3), 407-411. doi: 10.1046/j.1365-2672.1999.00677.x
CrossRef Google Scholar
|
|
[6]
|
S. A. Boone and C. P. Gerba, Significance of fomites in the spread of respiratory and enteric viral disease, Applied & Environmental Microbiology, 2007, 73(6), 1687-1696.
Google Scholar
|
|
[7]
|
T. Caraco and I. Wang, Free-living pathogens: Life-history constraints and strain competition, Journal of Theoretical Biology, 2008, 250(3), 569-579. doi: 10.1016/j.jtbi.2007.10.029
CrossRef Google Scholar
|
|
[8]
|
H. A. A. El-Saka, The fractional-order SIS epidemic model with variable population size, Journal of the Egyptian Mathematical Society, 2014, 22(1), 50-54. doi: 10.1016/j.joems.2013.06.006
CrossRef Google Scholar
|
|
[9]
|
K. Fushimi, Y. Enatsu and E. Ishiwata, Global stability of an SIS epidemic model with delays, Mathematical Methods in the Applied Sciences, 2018, 41(13), 5345-5354. doi: 10.1002/mma.5084
CrossRef Google Scholar
|
|
[10]
|
A. Gabbuti, L. Romanò, P. Blanc et al., Long-term immunogenicity of hepatitis B vaccination in a cohort of italian healthy adolescents, Vaccine, 2007, 25(16), 3129-3132. doi: 10.1016/j.vaccine.2007.01.045
CrossRef Google Scholar
|
|
[11]
|
H. Guo, M. Li and Z. Shuai, Global stability of the endemic equilibrium of multigroup SIR epidemic models, Canadian Applied Mathematics Quarterly, 2006, 14(3), 259-284.
Google Scholar
|
|
[12]
|
H. Huo, F. Cui and H. Xiang, Dynamics of an SAITS alcoholism model on unweighted and weighted networks, Physica A: Statistical Mechanics & Its Applications, 2018, 496, 249-262.
Google Scholar
|
|
[13]
|
H. Huo, P. Yang and H. Xiang, Dynamics for an SIRS epidemic model with infection age and relapse on a scale-free network, Journal of the Franklin Institute, 2019.
Google Scholar
|
|
[14]
|
H. F. Huo and L. X. Feng, Global stability of an epidemic model with incomplete treatment and vaccination, Discrete Dynamics in Nature and Society, 2012, 2012(1), 87-88.
Google Scholar
|
|
[15]
|
W. O. Kermack and A. G. McKendrick, A contribution to the mathematical theory of epidemics, Proceedings of The Royal Society of London. Series A. Mathematical, Physical and Engineering Sciences, 1927, 115, 700-721.
Google Scholar
|
|
[16]
|
T. Kuniya and J. Wang, Global dynamics of an SIR epidemic model with nonlocal diffusion, Nonlinear Analysis Real World Applications, 2018, 43, 262-282. doi: 10.1016/j.nonrwa.2018.03.001
CrossRef Google Scholar
|
|
[17]
|
J. P. Lasalle, The stability of dynamical systems, Regional Conference Series in Applied Mathematics, SIAM, Philadelphia, 1976. DOI: 10.1007/s13398-014-0173-7.2.
CrossRef Google Scholar
|
|
[18]
|
J. T. Lejeune, T. E. Besser and D. D. Hancock, Cattle water troughs as reservoirs of escherichia coli O157, Applied and Environmental Microbiology, 2001, 67(7), 3053-3057. doi: 10.1128/AEM.67.7.3053-3057.2001
CrossRef Google Scholar
|
|
[19]
|
J. Q. Li, Y. L. Yang and Y. C. Zhou, Global stability of an epidemic model with latent stage and vaccination, Nonlinear Analysis: Real World Applications, 2011, 12(4), 2163-2173. doi: 10.1016/j.nonrwa.2010.12.030
CrossRef Google Scholar
|
|
[20]
|
S. Liu, L. Zhang and Y. Xing, Dynamics of a stochastic heroin epidemic model, Journal of Computational and Applied Mathematics, 2019, 351, 260-269. doi: 10.1016/j.cam.2018.11.005
CrossRef Google Scholar
|
|
[21]
|
S. Liu, L. Zhang, X. Zhang and A. Li, Dynamics of a stochastic heroin epidemic model with bilinear incidence and varying population size, International Journal of Biomathematics, 2019, 12(1), 1950005(21 pages). doi: 10.1142/S1793524519500050
CrossRef Google Scholar
|
|
[22]
|
A. Ricardo, Analysis of a fractional SEIR model with treatment, Applied Mathematics Letters, 2018, 84, 56-62. doi: 10.1016/j.aml.2018.04.015
CrossRef Google Scholar
|
|
[23]
|
E. Scott and S. Bloomfield, The survival and transfer of microbial contamination via cloths, hands and utensils, Journal of Applied Bacteriology, 1990, 68(3), 271-278. doi: 10.1111/j.1365-2672.1990.tb02574.x
CrossRef Google Scholar
|
|
[24]
|
J. Tien and D. Earn, Multiple transmission pathways and disease dynamics in a waterborne pathogen model, Bulletin of Mathematical Biology, 2010, 72(6), 1506-1533. doi: 10.1007/s11538-010-9507-6
CrossRef Google Scholar
|
|
[25]
|
P. van den Driessche and J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Mathematical Biosciences, 2002, 180(1), 29-48.
Google Scholar
|
|
[26]
|
H. Xiang, Y. L. Tang and H. F. Huo, A viral model with intracellular delay and humoral immunity, Bulletin of the Malaysian Mathematical Sciences Society, 2017, 40(3), 1011-1023. doi: 10.1007/s40840-016-0326-2
CrossRef Google Scholar
|
|
[27]
|
H. Xiang, Y. Wang and H. Huo, Analysis of the binge drinking models with demographics and nonlinear infectivity on networks, Journal of Applied Analysis & Computation, 2018, 8(5), 1535-1554.
Google Scholar
|
|
[28]
|
H. Xiang, M. Zou and H. Huo, Modeling the effects of health education and early therapy on tuberculosis transmission dynamics, International Journal of Nonlinear Sciences & Numerical Simulation, 2019, 20, 243-255.
Google Scholar
|
|
[29]
|
L. Zhang, S. Liu and X. Zhang, Aaymptonic behavior of a stochastic virus dynamics model with intracellular delay and humoral immunity, Journal of Applied Analysis and Computation, 2019, 9(4), 1425-1442.
Google Scholar
|
|
[30]
|
L. Zhang and Y. Xing, Extremal solutions for nonlinear first-order impulsive integro-differential dynamic equations, Mathematical Notes, 2019, 105(1), 124-132.
Google Scholar
|
|
[31]
|
S. X. Zhang and H. Guo, Global analysis of age-structured multi-stage epidemic models for infectious diseases, Applied Mathematics and Computation, 2018, 337, 214-233. doi: 10.1016/j.amc.2018.05.020
CrossRef Google Scholar
|




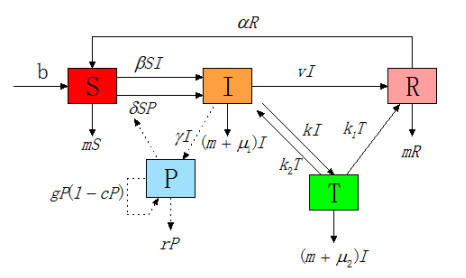

 DownLoad:
DownLoad: