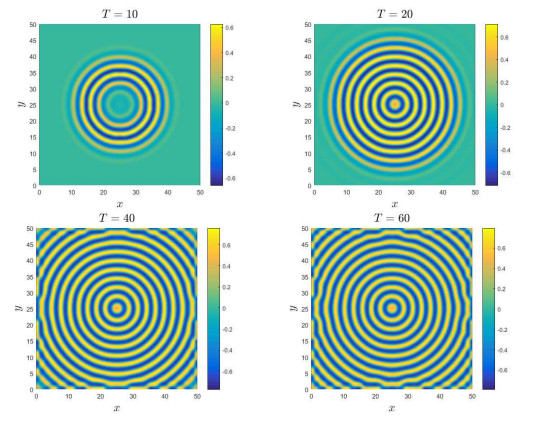
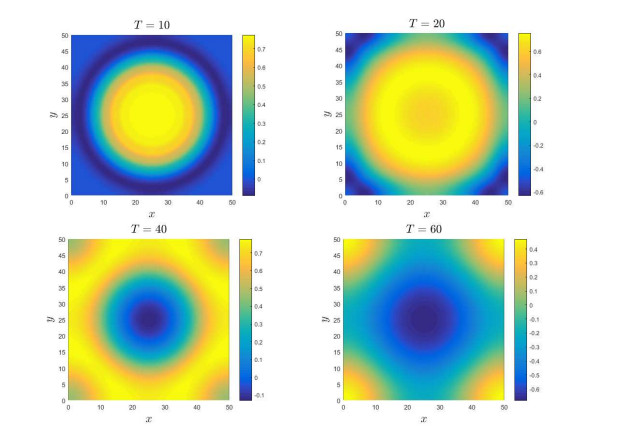
|
[1]
|
G. Bao and Z. Zeng, Analysis and design of associative memories based on recurrent neural network with discontinuous activation functions, Neurocomputing, 2012, 77(1), 101-107. doi: 10.1016/j.neucom.2011.08.026
CrossRef Google Scholar
|
|
[2]
|
L. O. Chua and L. Goraş, Turing patterns in cellular neural networks, International Journal of Electronics, 1995, 79(6), 719-736. doi: 10.1080/00207219508926307
CrossRef Google Scholar
|
|
[3]
|
T. Deb, A. K. Ghosh and A. Mukherjee, Singular value decomposition applied to associative memory of Hopfield neural network, Materials Today: Proceedings, 2018, 5(1), 2222-2228. doi: 10.1016/j.matpr.2017.09.222
CrossRef Google Scholar
|
|
[4]
|
K. Gopalsamy, Leakage delays in BAM, Journal of Mathathematical Analysis and Applications, 2007, 325(2), 1117-1132. doi: 10.1016/j.jmaa.2006.02.039
CrossRef Google Scholar
|
|
[5]
|
K. Gopalsamy, Stability and oscillations in delay differential equations of population dynamics, Kluwer Academic, Dordrecht, 1992.
Google Scholar
|
|
[6]
|
M. Garvie, Finite difference schemes for reaction-diffusion equations modeling predator-prey interactions in MATLAB, Bulletin of Mathematical Biology, 2007, 69(3), 931-956. doi: 10.1007/s11538-006-9062-3
CrossRef Google Scholar
|
|
[7]
|
B. Han and Z. Wang, Turing patterns of a Lotka-Volterra competitive system with nonlocal delay, International Journal of Bifurcation and Chaos, 2018, 28(7), 1830021. doi: 10.1142/S0218127418300215
CrossRef Google Scholar
|
|
[8]
|
C. Huang, L. Huang, J. Feng, M. Nai and Y. He, Hopf bifurcation analysis for a two-neuron network with four delays, Chaos, Solitons and Fractals, 2007, 34, 795-812. doi: 10.1016/j.chaos.2006.03.089
CrossRef Google Scholar
|
|
[9]
|
C. Huang, Y. He, L. Huang and Z. Yuan, Hopf bifurcation analysis of two neurons with three delays, Nonlinear Analysis: Real World Applications, 2007, 8(3), 903-921. doi: 10.1016/j.nonrwa.2006.03.014
CrossRef Google Scholar
|
|
[10]
|
C. Huang, Y. Meng, J. Cao, A. Alsaedi and F. Alsaadi, New bifurcation results for fractional BAM neural network with leakage delay, Chaos, Solitons and Fractals, 2017, 100, 31-44. doi: 10.1016/j.chaos.2017.04.037
CrossRef Google Scholar
|
|
[11]
|
C. Huang and J. Cao, Impact of leakage delay on bifurcation in high-order fractional BAM neural networks, Neural Networks, 2018, 98, 223-235. doi: 10.1016/j.neunet.2017.11.020
CrossRef Google Scholar
|
|
[12]
|
B. Kosko, Neural Networks and Fuzzy Systems, Prentice Hall, New Delhi, 1992.
Google Scholar
|
|
[13]
|
Z. Lin, D. Ma, J. Meng and L. Chen, Relative ordering learning in spiking neural network for pattern recognition, Neurocomputing, 2018, 275, 94-106. doi: 10.1016/j.neucom.2017.05.009
CrossRef Google Scholar
|
|
[14]
|
P. Melin and D. Sánchez, Multi-objective optimization for modular granular neural networks applied to pattern recognition, Information Sciences, 2017, 460-461, 594-610.
Google Scholar
|
|
[15]
|
T. Mikołajczyk, K. Nowicki, A. Bustillo and D.Y. Pimenov, Predicting tool life in turning operations using neural networks and image processing, Mechanical Systems and Signal Processing, 2018, 104, 503-513. doi: 10.1016/j.ymssp.2017.11.022
CrossRef Google Scholar
|
|
[16]
|
L. Olien and J. Bélair, Bifurcations, stability, and monotonicity properties of a delayed neural network model, Physica D, 1997, 102(3-4), 349-363. doi: 10.1016/S0167-2789(96)00215-1
CrossRef Google Scholar
|
|
[17]
|
Q. Ouyang, Patterns Formation in Reaction-diffusion Systems, Shanghai Science and Technology Education Press, Shanghai, 2000.
Google Scholar
|
|
[18]
|
R. Sakthivel, P. Vadivel, K. Mathiyalagan, A. Arunkumar and M. Sivachitra, Design of state estimator for bidirectional associative memory neural networks with leakage delays, Information Sciences, 2015, 296, 263-274. doi: 10.1016/j.ins.2014.10.063
CrossRef Google Scholar
|
|
[19]
|
Y. Seo and K. Shin, Hierarchical convolutional neural networks for fashion image classification, Expert Systems with Applications, 2019, 116, 328-339. doi: 10.1016/j.eswa.2018.09.022
CrossRef Google Scholar
|
|
[20]
|
X. Tian and R. Xu, Hopf bifurcation analysis of a reaction-diffusion neural network with time delay in leakage terms and distributed delays, Neural Processing Letters, 2016, 43(1), 173-193. doi: 10.1007/s11063-015-9410-0
CrossRef Google Scholar
|
|
[21]
|
X. Tian, R. Xu and Q. Gan, Hopf bifurcation analysis of a BAM neural network with multiple time delays and diffusion, Applied Mathematics and Computation, 2015, 266, 909-926. doi: 10.1016/j.amc.2015.06.009
CrossRef Google Scholar
|
|
[22]
|
A.M. Turing, The chemical basis of morphogenesis, Philosophical Transactions of the Royal Society B, 1952, 237(1-2), 37-72.
Google Scholar
|
|
[23]
|
S. Tyagi, S. Jain, S. Abbas, S. Meherrem and R. Ray, Time-delay-induced instabilities and Hopf bifurcation analysis in 2-neuron network model with reaction-diffusion term, Neurocomputing, 2018, 313, 306-315. doi: 10.1016/j.neucom.2018.06.008
CrossRef Google Scholar
|
|
[24]
|
Y. Wang, J. Cao, G. Sun and J. Li, Effect of time delay on pattern dynamics in a spatial epidemic model, Physica A, 2014, 412, 137-148. doi: 10.1016/j.physa.2014.06.038
CrossRef Google Scholar
|
|
[25]
|
Z. Wu, J. Li and J. Li, Pattern formations of an epidemic model with Allee effect and time delay, Chaos, Solitons and Fractals, 2017, 104, 599-606. doi: 10.1016/j.chaos.2017.09.028
CrossRef Google Scholar
|
|
[26]
|
J. Yang, L. Wang, Y. Wang and T. Guo, A novel memristive Hopfield neural network with application in associative memory, Neurocomputing, 2017, 227, 142-148. doi: 10.1016/j.neucom.2016.07.065
CrossRef Google Scholar
|
|
[27]
|
H. Yin and X. Wen, Pattern formation through temporal fractional derivatives, Scientific Reports, 2018, 8(1), 5070. doi: 10.1038/s41598-018-23470-8
CrossRef Google Scholar
|
|
[28]
|
H. Zhao, X. Huang and X. Zhang, Turing instability and pattern formation of neural networks with reaction-diffusion terms, Nonlinear Dynamics, 2014, 76, 115-124. doi: 10.1007/s11071-013-1114-2
CrossRef Google Scholar
|
|
[29]
|
X. Zhang, G. Sun and Z. Jin, Spatial dynamics in a predator-prey model with Beddington-DeAngelis functional response, Physical Review E, 2012, 85(2), 021924. doi: 10.1103/PhysRevE.85.021924
CrossRef Google Scholar
|
|
[30]
|
Q. Zheng and J. Shen, Dynamics and pattern formation in a cancer network with diffusion, Communications in Nonlinear Science and Numerical Simulation, 2015, 27(1-3), 93-109. doi: 10.1016/j.cnsns.2015.02.023
CrossRef Google Scholar
|
|
[31]
|
Q. Zheng and J. Shen, Pattern formation in the FitzHugh-Nagumo model, Computers and Mathematics with Applications, 2015, 70(5), 1082-1097. doi: 10.1016/j.camwa.2015.06.031
CrossRef Google Scholar
|




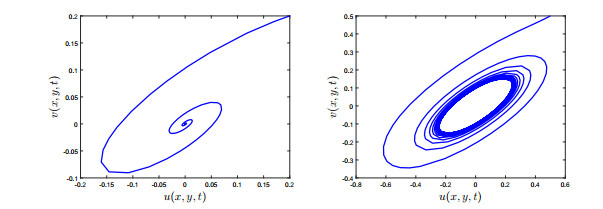

 DownLoad:
DownLoad: