| Citation: |
Li Jin, Yunxian Dai, Yu Xiao, Yiping Lin. RANK-ONE CHAOS IN A DELAYED SIR EPIDEMIC MODEL WITH NONLINEAR INCIDENCE AND TREATMENT RATES[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 1779-1801. doi: 10.11948/20200190
|
RANK-ONE CHAOS IN A DELAYED SIR EPIDEMIC MODEL WITH NONLINEAR INCIDENCE AND TREATMENT RATES
-
Abstract
The rank one chaos in a SIR model with two time-delays is studied in this paper. By using center manifold theorem, normal form theory and Hassard's method, the existence, direction and stability of Hopf bifurcation are discussed. Based on the rank-one chaos theory for delayed differential equations, the conditions for the existence of rank-one strange attractor in disturbed system are obtained. Finally, numerical simulations are given to verify the theoretical analysis results.
-
-
References
[1] F. Chen and M. Han, Rank one chaos in a class of planar systems with hete-roclinic cycle, Chaos, 2009, 19(4), 043122. doi: 10.1063/1.3263945 [2] Y. Dai, Y. Lin, W. Yang and H. Zhao, Rank one chaos in periodically-kicked time-delayed Chen system, International Journal of Bifurcation and Chaos, 2015, 25(8), 1550097. doi: 10.1142/S0218127415500972 [3] B. Dubey, A. Patra, P. K. Srivastava and U. S. Dubey, Modeling and analysis of an SEIR model with different types of nonlinear treatment rates, Journal of Biological Systems, 2013, 21(3), 1350023. doi: 10.1142/S021833901350023X [4] K. Goel and Nilam, A mathematical and numerical study of a SIR epidemic model with time delay, nonlinear incidence and treatment rates, Theory in Biosciences, 2019, 138(2), 203-213. doi: 10.1007/s12064-019-00275-5 [5] D. Gao and N. Huang, Threshold dynamics of an SEIR epidemic model with a nonlinear incidence rate and a discontinuous treatment function, Revista De La Real Academia De Ciencias Exactas Fisicas Y Naturales Serie A-matematicas, 2019, 114(1), 5. doi: 10.1007/s13398-019-00751-z [6] K. Goel and Nilam, Stability behavior of a nonlinear mathematical epidemic transmission model with time delay, Nonlinear Dynamics, 2019, 98(2), 1501-1518. doi: 10.1007/s11071-019-05276-z [7] J. Hale, Theory of Functional Differential Equations, Springer, New York, 1977. [8] B. D. Hassard, N. D. Kazarinoff and Y. Wan, Theory and applications of Hopf bifurcation, Cambridge University Press, London, 1981. [9] W. O. Kermack and A. G. Mckendrick, A contribution to the mathematical the-ory of epidemics, Proceedings of The Royal Society A: Mathematical, Physical and Engineering Sciences, 1927, 115, 700-721. doi: 10.1007/BF02464424 [10] A. Kumar and Nilam, Stability of a time delayed SIR epidemic model along with nonlinear incidence rate and Holling type-II treatment rate, International Journal of Computational Methods, 2018, 15(6), 1850055. doi: 10.1142/S021987621850055X [11] A. Kumar and Nilam, Mathematical analysis of a delayed epidemic model with nonlinear incidence and treatment rates, Journal of Engineering Mathematics, 2019, 115(1), 1-20. doi: 10.1007/s10665-019-09989-3 [12] Y. A. Kuznetsov, Elements of Applied Bifurcation Theory, Springer, New York, 1995. [13] W. Liu, S. A. Levin and Y. Iwasa, Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models, Journal of Mathematical Biology, 1986, 23(2), 187-204. doi: 10.1007/BF00276956 [14] Z. Luo, Y. Lin and Y. Dai, Strange attractors in periodically kicked predator-prey system with discrete and distributed delay, Chaos Solitons and Fractals, 2016, 93, 80-88. doi: 10.1016/j.chaos.2016.10.008 [15] A. Oksasoglu and Q. Wang, Rank one chaos in a switch-controlled Chua's cir-cuit, Journal of The Franklin Institute-engineering and Applied Mathematics, 2010, 347(9), 1598-1622. doi: 10.1016/j.jfranklin.2010.06.006 [16] F. Rao, P. S. Mandal and Y. Kang, Complicated endemics of an SIRS model with a generalized incidence under preventive vaccination and treatment con-trols, Applied Mathematical Modelling, 2019, 67, 38-61. doi: 10.1016/j.apm.2018.10.016 [17] S. Ruan and J. Wei, On the zeros of transcendental functions with applications to stability of delay differential equations with two delays, Dynamics of Con-tinuous Discrete and Impulsive Systems-series A-mathematica Analysis, 2003, 10(6), 863-874. [18] R. K. Upadhyay, A. K. Pal, S. Kumari and P. Roy, Dynamics of an SEIR epidemic model with nonlinear incidence and treatment rates, Nonlinear Dy-namics, 2019, 96(4), 2351-2368. doi: 10.1007/s11071-019-04926-6 [19] Q. Wang and L. Young, Strange attractors with one direction of instability, Communications in Mathematical Physics, 2001, 218(1), 1-97. doi: 10.1007/s002200100379 [20] Q. Wang and L. Young, From invariant curves to strange attractors, Commu-nications in Mathematical Physics, 2002, 225(2), 275-304. doi: 10.1007/s002200100582 [21] Q. Wang and L. Young, Strange attractors in periodically-kicked limit cycles and Hopf bifurcations, Communications in Mathematical Physics, 2003, 240(3), 509-529. doi: 10.1007/s00220-003-0902-9 [22] Q. Wang and A. Oksasoglu, Strange attractors in periodically kicked Chua's circuit, International Journal of Bifurcation and Chaos, 2005, 15(1), 83-98. doi: 10.1142/S0218127405012028 [23] X. Wang, A simple proof of descartes's rule of signs, American Mathematical Monthly, 2004, 111(6), 525-526. doi: 10.1080/00029890.2004.11920108 [24] P. Yang, J. Fang, Y. Dai and Y. Lin, Rank-one chaos in a periodically kicked three-species food chain with time-delay, International Journal of Bifurcation and Chaos, 2020, 30(3), 2050038. doi: 10.1142/S0218127420500388 [25] W. Yang, Y. Lin, Y. Dai and H. Zhao, Rank one strange attractors in peri-odically kicked predator-prey system with time-delay, International Journal of Bifurcation and Chaos, 2016, 26(7), 1650114. [26] W. Yang, Y. Lin, Y. Dai and Y. Jia, Rank one strange attractors in periodically kicked Chua's system with time delay, Advances in Difference Equations, 2015, 2015: 75. doi: 10.1186/s13662-015-0397-7 [27] W. Yang, Y. Lin and Y. Dai, Rank one strange attractors in periodically kicked Lorenz system with time-delay, Discrete Dynamics in Nature and Society, 2015, 2015, 915614. -
-
Figures(12)
Export File
Citation
Li Jin, Yunxian Dai, Yu Xiao, Yiping Lin. RANK-ONE CHAOS IN A DELAYED SIR EPIDEMIC MODEL WITH NONLINEAR INCIDENCE AND TREATMENT RATES[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 1779-1801. doi: 10.11948/20200190
Format
Content
DownLoad:
-
Figure 1.
$ E $ is locally asymptotically stable with$ \varepsilon = 0 $ ,$ \tau_{1} = \tau_{2} = 0 $ -
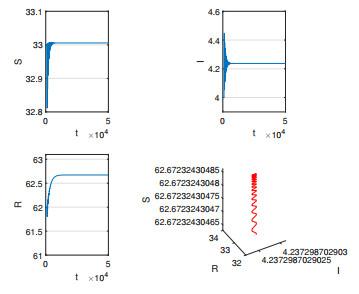
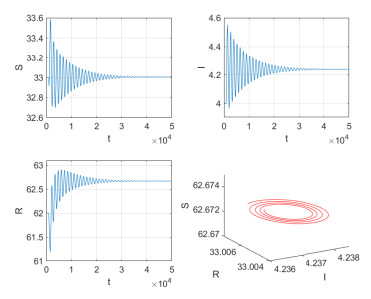
Figure 2.
$ E $ is asymptotically stable with$ \varepsilon = 0 $ ,$ \tau_{1} = 0 $ ,$ \tau_{2} = 5 $ . -
Figure 3. A Hopf bifurcation occurs from
$ E $ with$ \varepsilon = 0 $ ,$ \tau_{1} = 0,\tau_{2} = 7.14 $ . -
Figure 4.
$ E $ is asymptotically stable with$ \varepsilon = 0 $ ,$ \tau = 0.9 $ . -
Figure 5. A Hopf bifurcation occurs from
$ E $ with$ \varepsilon = 0 $ ,$ \tau = 1.04 $ . -
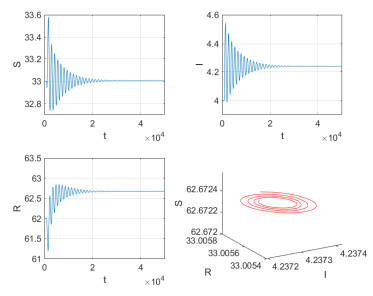
Figure 6.
$ E $ is asymptotically stable with$ \varepsilon = 0 $ ,$ \tau_{1} = 0.2 $ ,$ \tau_{2} = 5 $ . -
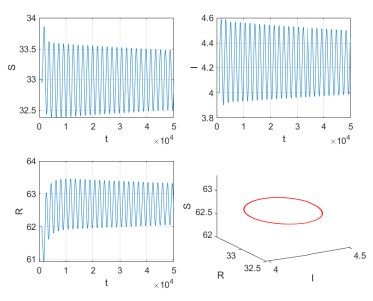
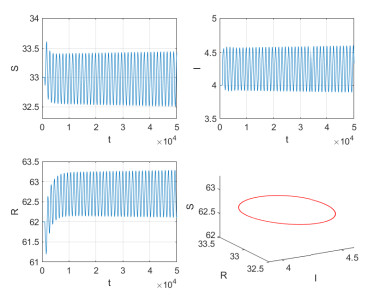
Figure 7. Stable periodic solutions bifurcate from
$ E $ with$ \varepsilon = 0 $ ,$ \tau_{1} = 0.56 $ ,$ \tau_{2} = 5 $ . -
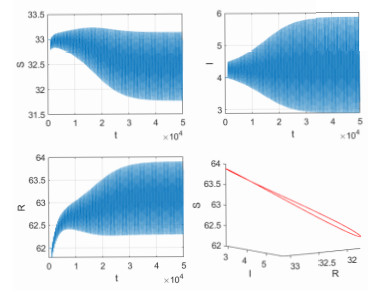
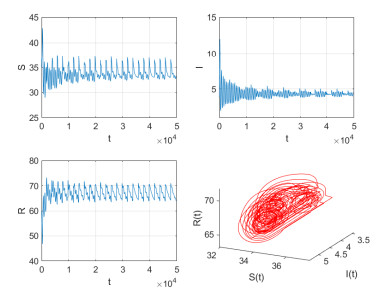
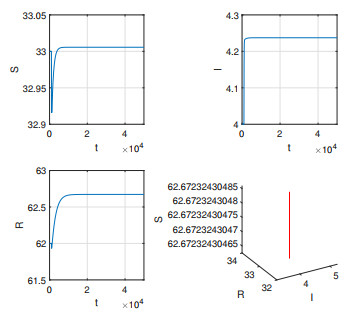
Figure 8.
$ E $ is unstable, and a rank-one strange attractor occurs with$ \tau_{1} = 0.56 $ ,$ \tau_{2} = 5 $ ,$ \varepsilon = 0.1 $ ,$ T = 2000 $ . -
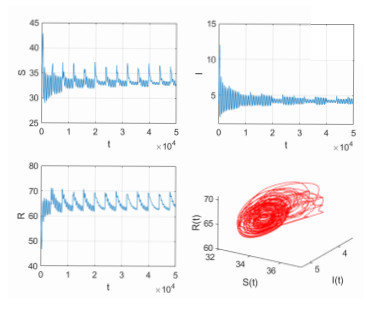
Figure 9.
$ E $ is unstable, and a rank-one strange attractor occurs with$ \tau_{1} = 0.56 $ ,$ \tau_{2} = 5 $ ,$ \varepsilon = 0.1 $ ,$ T = 4000 $ . -
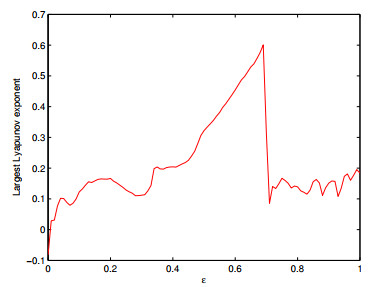
Figure 10. Largest Lyapunov exponent
$ \lambda $ versus$ \varepsilon $ with$ \tau_{1} = 0.56 $ ,$ \tau_{2} = 5 $ ,$ T = 2000 $ ,$ \varepsilon $ varying from$ 0 $ to$ 1 $ . -
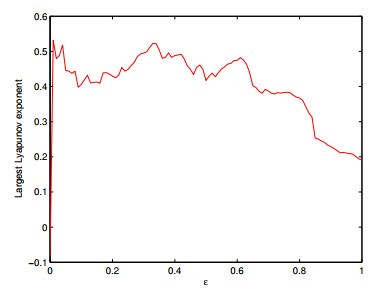
Figure 11. Largest Lyapunov exponent
$ \lambda $ versus$ \varepsilon $ with$ \tau_{1} = 0.56 $ ,$ \tau_{2} = 5 $ ,$ T = 4000 $ ,$ \varepsilon $ varying from$ 0 $ to$ 1 $ . -
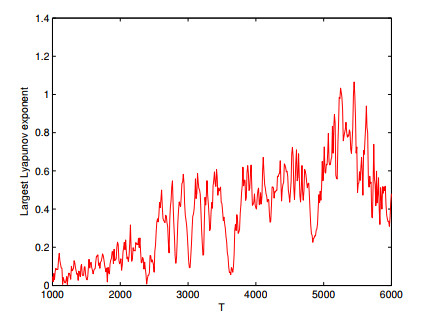
Figure 12. Largest Lyapunov exponent
$ \lambda $ versus$ T $ with$ \tau_{1} = 0.56 $ ,$ \tau_{2} = 5 $ ,$ \varepsilon = 0.1 $ ,$ T $ varying from$ 1000 $ to$ 6000 $