| Citation: | Dongpo Hu, Ying Zhang, Zhaowen Zheng, Ming Liu. DYNAMICS OF A DELAYED PREDATOR-PREY MODEL WITH CONSTANT-YIELD PREY HARVESTING[J]. Journal of Applied Analysis & Computation, 2022, 12(1): 302-335. doi: 10.11948/20210171 |
DYNAMICS OF A DELAYED PREDATOR-PREY MODEL WITH CONSTANT-YIELD PREY HARVESTING
-
Abstract
In this paper, we study a delayed predator-prey model of Holling and Leslie type with constant-yield prey harvesting, in which two types of delays caused by maturation time of prey and the gestation time of predator are considered. We mainly investigate the local dynamics of the model with emphasis on the impact of delays. The stability of equilibrium and the existence conditions of Hopf bifurcation are discussed. First, based on the different values of delays, five cases of Hopf bifurcation are studied in detail. The critical values of Hopf bifurcation for each case are presented. In addition, we explore the properties of Hopf bifurcation. The direction of Hopf bifurcation and the stability of periodic solutions by using the normal form theory and central manifold theorem are determined. The qualitative analyses have demonstrated that the values of time delays can affect the stability of equilibrium and induce small amplitude period oscillations of population densities. Numerical simulations are carried out for illustrating the theoretical results. Meanwhile, we further investigate the effects of delay on the period of periodic solutions and the influence of the harvesting term on the stability of the equilibrium with time delays.
-
Keywords:
- Predator-prey model /
- time delay /
- stability /
- Hopf bifurcation
-

-
References
[1] S. Boonrangsiman, K. Bunwong and E.J. Moore, A bifurcation path to chaos in a time-delay fisheries predator-prey model with prey consumption by immature and mature predators, Math. Comput. Simulat., 2016, 124: 16–29. doi: 10.1016/j.matcom.2015.12.009 [2] I. Boudjema and S. Djilali, Turing-Hopf bifurcation in Gauss-type model with cross diffusion and its application, Nonlinear Stud., 2018, 25: 665–687. [3] L. Chang, G. Sun, Z. Wang and Z. Jin, Rich dynamics in a spatial predator-prey model with delay, Appl. Math. Comput., 2015, 256, 540–550. [4] J. Chen, J. Huang, S. Ruan and J. Wang, Bifurcations of invariant tori in predator-prey models with seasonal prey harvesting, SIAM J. Appl. Math., 2013, 73, 1876–1905. doi: 10.1137/120895858 [5] J. M. Cushing, Integrodifferential equations and delay models in population dynamics, Springer-Verlag, Berlin Heidelberg New York, 1977. [6] E. N. Dancer and Y. Du, Effects of certain degeneracies in the predator-prey model, SIAM J. Math. Anal., 2002, 34, 292–314. doi: 10.1137/S0036141001387598 [7] S. Djilali, Effect of herd shape in a diffusive predator-prey model with time delay, J. Appl. Anal. Comput., 2019, 9, 638–654. [8] S. Djilali, Herd behavior in a predator-prey model with spatial diffusion: bifurcation analysis and Turing instability, J. Appl. Math. Comput., 2018, 58, 125–149. doi: 10.1007/s12190-017-1137-9 [9] S. Djilali, Impact of prey herd shape on the predator-prey interaction, Chaos Solitons Fract., 2019, 120, 139–148. doi: 10.1016/j.chaos.2019.01.022 [10] S. Djilali, Pattern formation of a diffusive predator-prey model with herd behavior and nonlocal prey competition, Math. Meth. Appl. Sci., 2020, 43, 2233–2250. doi: 10.1002/mma.6036 [11] S. Djilali, Spatiotemporal patterns induced by cross-diffusion in predator-prey model with prey herd shape effect, Int. J. Biomath., 2020, 13, Article ID 2050030. doi: 10.1142/S1793524520500308 [12] S. Djilali and S. Bentout, Spatiotemporal patterns in a diffusive predator-prey model with prey social behavior, Acta. Appl. Math., 2020, 169, 125–143. doi: 10.1007/s10440-019-00291-z [13] S. Djilali and B. Ghanbari, The influence of an infectious disease on a prey-predator model equipped with a fractional-order derivative, Adv. Differ. Equ., 2021, 2021, 20. doi: 10.1186/s13662-020-03177-9 [14] S. Djilali, B. Ghanbari, S. Bentout and A. Mezouaghi, Turing-Hopf bifurcation in a diffusive mussel-algae model with time-fractional-order derivative, Chaos Solitons Fract., 2020, 138, Article ID 109954. doi: 10.1016/j.chaos.2020.109954 [15] Y. Du, B. Niu and J. Wei, Two delays induce Hopf bifurcation and double Hopf bifurcation in a diffusive Leslie-Gower predator-prey system, Chaos, 2019, 29, Article ID 013101. [16] B. Hassard, N. Kazarinoff and Y. Wan, Theory and applications of Hopf bifurcation, Cambridge Univ. Press, Cambridge, 1981. [17] S. B. Hsu and T. Huang, Global stability for a class of predator-prey systems, SIAM J. Appl. Math., 1995, 55, 763–783. doi: 10.1137/S0036139993253201 [18] S. B. Hsu and T. Huang, Hopf bifurcation analysis for a predator-prey system of Holling and Leslie type, Taiwanese J. Math., 1999, 3, 35–53. [19] S. B. Hsu and T. Huang, Uniqueness of limit cycles for a predator-prey system of Holling and Leslie type, Canad. Appl. Math. Quart., 1998, 6, 91–117. [20] D. Hu and H. Cao, Bifurcation and chaos in a discrete-time predator-prey system of Holling and Leslie type, Commun. Nonlinear Sci. Numer. Simulat., 2015, 22, 702–715. doi: 10.1016/j.cnsns.2014.09.010 [21] D. Hu and H. Cao, Stability and bifurcation analysis in a predator-prey system with Michaelis-Menten type predator harvesting, Nonlinear Anal: Real, 2017, 33, 58–82. doi: 10.1016/j.nonrwa.2016.05.010 [22] D. Hu, Y. Li, M. Liu and Y. Bai, Stability and Hopf bifurcation for a delayed predator-prey model with stage structure for prey and Ivlev-type functional response, Nonlinear Dynam., 2020, 99, 3323–3350. doi: 10.1007/s11071-020-05467-z [23] C. Huang, J. Cao, M. Xiao, A. Alsaedi and F. E. Alsaadi, Controlling bifurcation in a delayed fractional predator-prey system with incommensurate orders, Appl. Math. Comput., 2017, 293, 293–310. [24] C. Huang, H. Li and J. Cao, A novel strategy of bifurcation control for a delayed fractional predator-prey model, Appl. Math. Comput., 2019, 347, 808–838. [25] J. Huang, Y. Gong and J. Chen, Multiple bifurcations in a predator-prey system of Holling and Leslie type with constant-yield prey harvesting, Int. J. Bifurcat. Chaos, 2013, 23, Article ID 1350164. doi: 10.1142/S0218127413501642 [26] X. Jiang, X. Chen, T. Huang and H. Yan, Bifurcation and control for a predator-prey system with two delays, Circuits and Systems II: Express Briefs, IEEE Transactions, 2020, 99, 1–5. [27] H. Kharbanda and S. Kumar, Chaos detection and optimal control in a cannibalistic prey-predator system with harvesting, Int. J. Bifurcat. Chaos, 2020, 30, Article ID 2050171. doi: 10.1142/S0218127420501710 [28] C. J. Krebs, Ecology: The Experimental Analysis of Distribution and Abundance, Pearson New international edition, 6th ed, 2014, [29] Y. Kuang, Delay differential equations with applications in population dynamics. Academic Press, Boston, Math. Comput. Simulat., 1993. [30] S. Kundu and S. Maitra, Dynamical behaviour of a delayed three species predator-prey model with cooperation among the prey species, Nonlinear Dynam., 2018, 92, 627–643. doi: 10.1007/s11071-018-4079-3 [31] X. Li and S. Huang, Stability and bifurcation for a single-species model with delay weak kernel and constant rate harvesting, Complexity, 2019, 2019, Article ID 1810385. [32] M. Liu, Dynamics of a stochastic regime-switching predator-prey model with modified Leslie-Gower Holling-type II schemes and prey harvesting, Nonlinear Dynam., 2019, 96, 417–442. doi: 10.1007/s11071-019-04797-x [33] M. Liu, D.P. Hu and F.W. Meng, Stability and bifurcation analysis in a delay-induced predator-prey model with Michaelis-Menten type predator harvesting, Discrete Cont. Dyn. S, 2021, 14, 3197–3222. [34] W. Liu and Y. Jiang, Bifurcation of a delayed Gause predator-prey model with Michaelis-Menten type harvesting, J. Theor. Bio., 2018, 438, 116–132. doi: 10.1016/j.jtbi.2017.11.007 [35] J. Luo and Y. Zhao, Stability and bifurcation analysis in a predator-prey system with constant harvesting and prey group defense, Int. J. Bifurcat. Chaos, 2017, 27, Article ID 1750179. doi: 10.1142/S0218127417501796 [36] Y. Lv, Y. Pei and Y. Wang, Bifurcations and simulations of two predator-prey models with nonlinear harvesting, Chaos, Solitons Fract., 2019, 120, 158–170. doi: 10.1016/j.chaos.2018.12.038 [37] Z. Ma, Hopf bifurcation of a generalized delay-induced predator-prey system with habitat complexity, Int. J. Bifurcat. Chaos, 2020, 30, 2050082. doi: 10.1142/S0218127420500820 [38] A. Ojha and N. K. Thakur, Exploring the complexity and chaotic behavior in plankton-fish system with mutual interference and time delay, BioSystems, 2020, 198, 104283. doi: 10.1016/j.biosystems.2020.104283 [39] B. Sahoo and S. Poria, Effects of supplying alternative food in a predator-prey model with harvesting, Appl. Math. Comput., 2014, 234, 150–166. [40] F. Souna, S. Djilali and F. Charif, Mathematical analysis of a diffusive predator-prey model with herd behavior and prey escaping, Math. Model. Nat. Phenom., 2020, 15, 23. doi: 10.1051/mmnp/2019044 [41] F. Souna, A. Lakmeche and S. Djilali, Spatiotemporal patterns in a diffusive predator-prey model with protection zone and predator harvesting, Chaos, Soliton. Fract., 2020, 140, Article ID 110180. doi: 10.1016/j.chaos.2020.110180 [42] F. Souna, A. Lakmeche and S. Djilali, The effect of the defensive strategy taken by the prey on predator-prey interaction, J. Appl. Math. Comput., 2020, 64, 665–690. doi: 10.1007/s12190-020-01373-0 [43] S. H. Strogatz, Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering, CRC Press, 2018. [44] V. Tiwari, J. P. Tripathi, S. Abbas, J. Wang, G. Sun and Z. Jin, Qualitative analysis of a diffusive Crowley-Martin predator-prey model: the role of nonlinear predator harvesting, Nonlinear Dynam., 2019, 98, 1169–1189. doi: 10.1007/s11071-019-05255-4 [45] R. K. Upadhyay and R. Agrawal, Dynamics and responses of a predator-prey system with competitive interference and time delay, Nonlinear Dynam., 2016, 83, 821–837. doi: 10.1007/s11071-015-2370-0 [46] D. Wilson and J. Moehlis, Isostable reduction of periodic orbits, Phys. Rev., 2016, E94, 052213. [47] C. Xiang, J. Huang, S. Ruan and D. Xiao, Bifurcation analysis in a host-generalist parasitoid model with Holling II funcational response, J. Diff. Eqs, 2020, 268, 4618–4662. doi: 10.1016/j.jde.2019.10.036 [48] D. Xiao and L. S. Jennings, Bifurcations of a ratio-dependent predator-prey system with constant rate harvesting, SIAM J. Appl. Math., 2005, 65, 737–753. doi: 10.1137/S0036139903428719 -
-
-
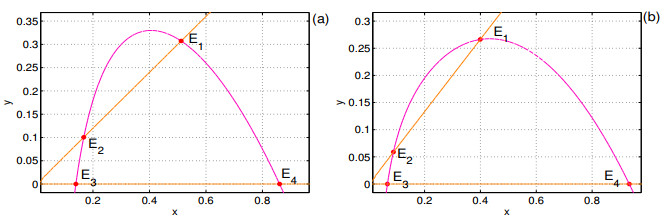
Figure 1. The equilibria of model (2.1). The magenta and yellow lines represent prey and predator nullclines, respectively. The points where the two nullclines cross are equilibria and there are four of these points for (a)
$ a = 0.7 $ ,$ h = \frac{3}{25} $ ,$ \delta = \frac{3}{5} $ ,$ \beta = 1 $ ; (b)$ a = 0.2 $ ,$ h = \frac{1}{16} $ ,$ \delta = \frac{1}{5} $ ,$ \beta = 0.3 $ . -
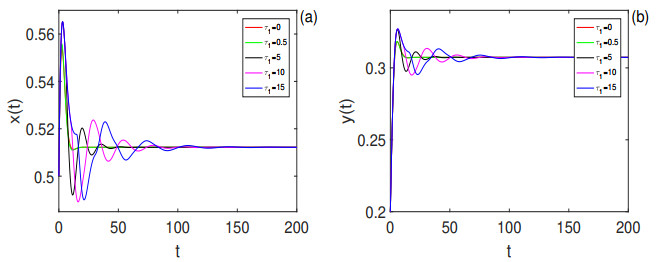
Figure 2. Time series of
$ x(t) $ ,$ y(t) $ of model (2.1) with$ \tau_2 = 0 $ and$ \tau_1 = 0, 0.5, 5, 10, 15 $ , respectively. The positive equilibrium$ E_1(0.51219177, 0.30731719) $ is locally asymptotically stable. Here the initial value is$ (0.5, 0.2). $ . -
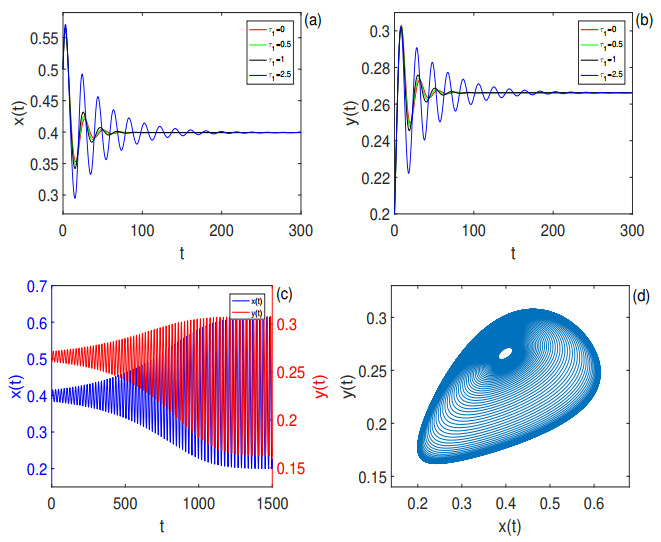
Figure 3. (a)-(b): Time series of
$ x(t) $ ,$ y(t) $ of model (2.1) with$ \tau_2 = 0 $ and$ \tau_1 = 0, 0.5, 1, 2.5 < \tau_{1_0} = 3.11596840 $ , respectively. The positive equilibrium$ E_1(0.39929087, 0.26619585) $ is locally asymptotically. The initial value is$ (0.5, 0.2) $ . (c)-(d): Time series of$ x(t) $ ,$ y(t) $ and phase portrait of model (2.1) with$ \tau_2 = 0 $ and$ \tau_1 = 3.2 > \tau_{1_0} = 3.11596840 $ . The positive equilibrium$ E_1 $ is unstable and the orbit from the initial value$ (0.39, 0.26) $ located in a sufficiently small neighborhood of$ E_1 $ converges to a periodic solution. -
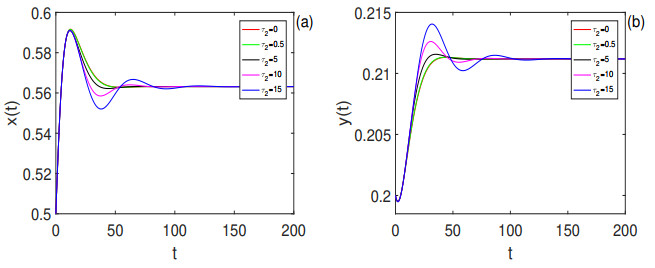
Figure 4. Time series of
$ x(t) $ ,$ y(t) $ of model (2.1) with$ \tau_1 = 0 $ and$ \tau_2 = 0, 0.5, 5, 10, 15 $ , respectively. The positive equilibrium$ E_1(0.56316894, 0.21118835) $ is locally asymptotically stable. Here initial value is$ (0.5, 0.2) $ . -
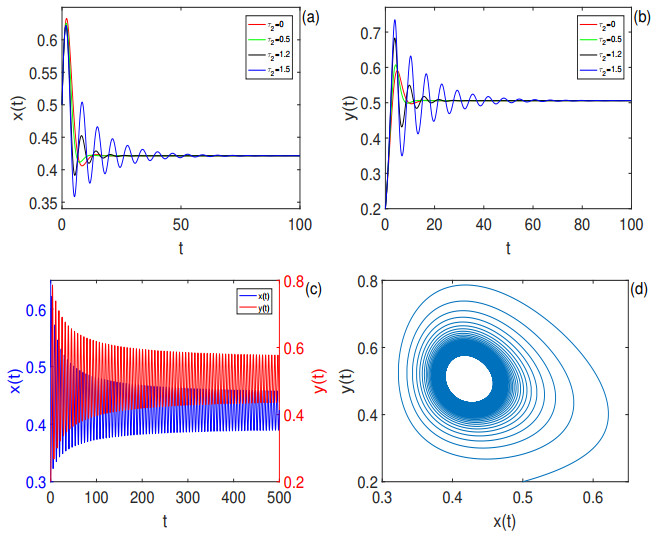
Figure 5. (a)-(b): Time series of
$ x(t) $ ,$ y(t) $ of model (2.1) with$ \tau_1 = 0 $ and$ \tau_2 = 0, 0.5, 1.2, 1.5 < \tau_{2_0} = 1.76144387 $ , respectively. The positive equilibrium$ E_1(0.42147248, 0.50576827) $ is locally asymptotically. The initial value is$ (0.5, 0.2) $ . (c)-(d): Time series of$ x(t) $ ,$ y(t) $ and phase portrait of model (2.1) with$ \tau_1 = 0 $ and$ \tau_2 = 1.77 > \tau_{2_0} = 1.76144387 $ . The positive equilibrium$ E_1 $ is unstable and the orbit from the initial value$ (0.5, 0.2) $ located in a sufficiently small neighborhood of$ E_1 $ converges to a periodic solution. -
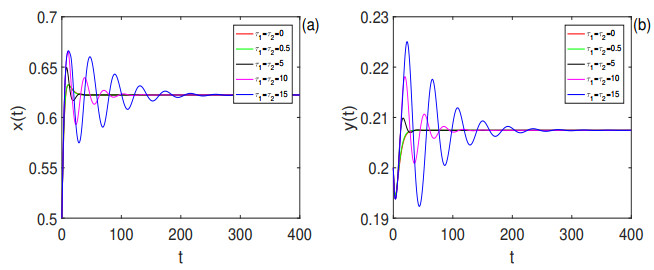
Figure 6. Time series of
$ x(t) $ ,$ y(t) $ of model (2.1) with$ \tau_1 = \tau_2 = 0, 0.5, 5, 10, 15 $ , respectively. The positive equilibrium$ E_1(0.62234655, 0.20744885) $ is locally asymptotically stable. Here initial value is$ (0.5, 0.2) $ . -
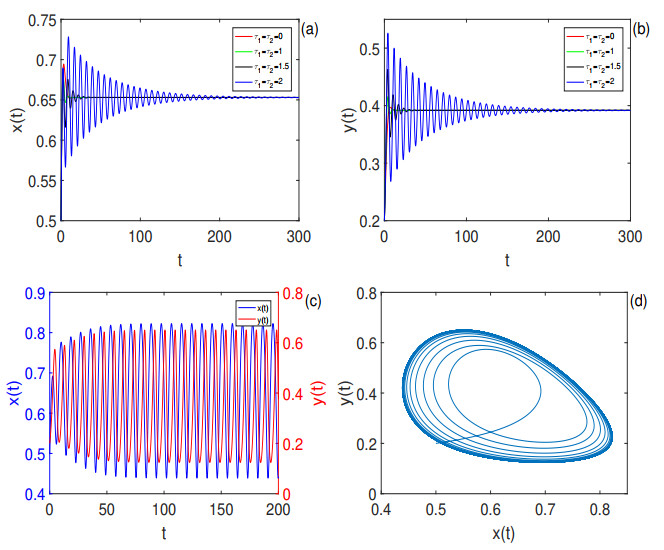
Figure 7. (a)-(b): Time series of
$ x(t) $ ,$ y(t) $ of model (2.1) with$ \tau_1 = \tau_2 = 0, 1, 1.5, 2 < \tau_{3_0} = 2.12332287 $ , respectively. The positive equilibrium$ E_1(0.65299477, 0.39179686) $ is locally asymptotically. The initial value is$ (0.5, 0.2) $ . (c)-(d): Time series of$ x(t) $ ,$ y(t) $ and phase portrait of model (2.1) with$ \tau_1 = \tau_2 = 2.35 > \tau_{3_0} = 2.12332287 $ . The positive equilibrium$ E_1 $ is unstable and the orbit from the initial value$ (0.5, 0.2) $ located in a sufficiently small neighborhood of$ E_1 $ converges to a periodic solution. -
Figure 8. Time series of
$ x(t) $ ,$ y(t) $ of model (2.1) with$ \tau_2 = 1 $ and$ \tau_1 = 0, 0.5, 5, 10, 15 $ , respectively. The positive equilibrium$ E_1(0.60848685, 0.17385342) $ is locally asymptotically stable. Here initial value is$ (0.5, 0.2) $ . -
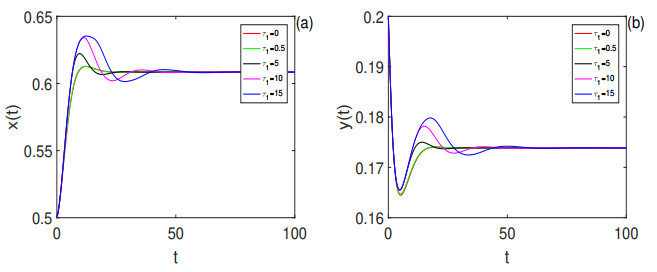
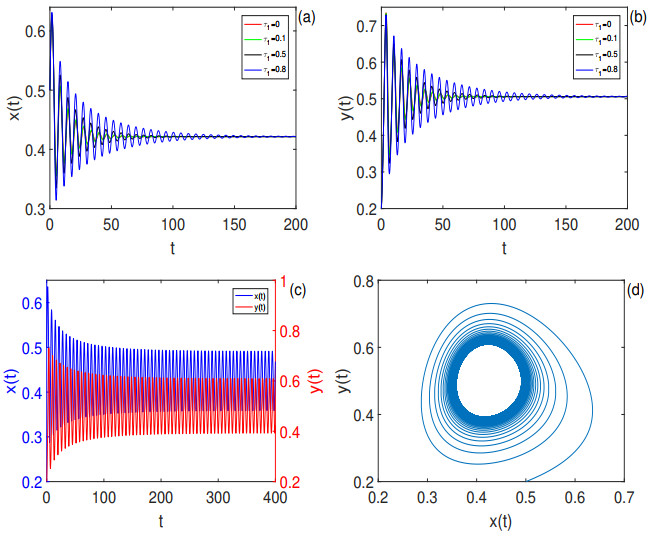
Figure 9. (a)-(b): Time series of
$ x(t) $ ,$ y(t) $ of model (2.1) with$ \tau_2 = 1.5 $ and$ \tau_1 = 0, 0.1, 0.5, 0.8 < \tau_{4_0} = 1.08245692 $ , respectively. The positive equilibrium$ E_1(0.42147248, 0.50576827) $ is locally asymptotically. The initial value is$ (0.5, 0.2) $ . (c)-(d): Time series of$ x(t) $ ,$ y(t) $ and phase portrait of model (2.1) with$ \tau_2 = 1.5 $ and$ \tau_1 = 1.15 > \tau_{4_0} = 1.08245692 $ . The positive equilibrium$ E_1 $ is unstable and the orbit from the initial value$ (0.5, 0.2) $ located in a sufficiently small neighborhood of$ E_1 $ converges to a periodic solution. -
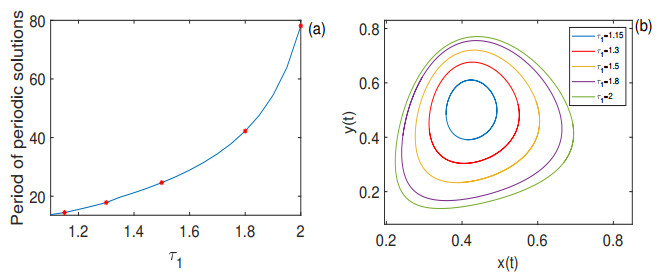
Figure 10. (a): The effect of
$ \tau_1 $ on the period$ T_2 $ with$ \tau_2 = 1.5\in[0, \tau_{2_0}) $ . The stars stand for$ \tau_1 = 1.15, 1.3, 1.5, 1.8, 2 > \tau_{4_0} = 1.08245692 $ , respectively. (b): Phase portraits without showing the transient of model (2.1) with$ \tau_2 = 1.5\in[0, \tau_{2_0}) $ and$ \tau_1 = 1.15, 1.3, 1.5, 1.8, 2 > \tau_{4_0} = 1.08245692 $ , respectively. The parameters are the same as Fig. 9. -
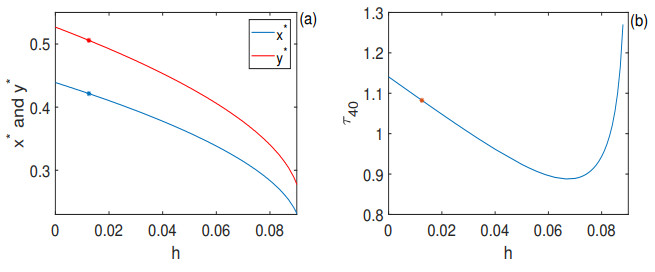
Figure 11. (a): The relationship between the location of the positive equilibrium
$ E_1(x^*, y^*) $ and$ h $ . The blue and red stars stand for$ (\frac{1}{80}, 0.42147248) $ and$ (\frac{1}{80}, 0.50576827) $ , respectively. (b): The relationship between the critical value$ \tau_{4_0} $ and$ h $ . The red star is$ (\frac{1}{80}, 1.08245692) $ .




 DownLoad:
DownLoad: