| Citation: |
Yue Li, Hongjun Cao. BIFURCATION AND COMPARISON OF A DISCRETE-TIME HINDMARSH-ROSE MODEL[J]. Journal of Applied Analysis & Computation, 2023, 13(1): 34-56. doi: 10.11948/20210204
|
BIFURCATION AND COMPARISON OF A DISCRETE-TIME HINDMARSH-ROSE MODEL
-
Abstract
In this paper, a Hindmarsh-Rose model discretized by a nonstandard finite difference (NSFD) scheme is considered. Bifurcation behaviors are compared between the model obtained by the forward Euler scheme and the model obtained by the NSFD scheme. Through analytical and numerical comparisons, the Neimark-Sacker bifurcation of the model discretized by the NSFD method is closer to the Hopf bifurcation of the original continuous Hindmarsh-Rose model than that discretized by the forward Euler method. Moreover, due to the NSFD method's better stability and convergence, the integral step size can be chosen larger in the NSFD scheme. And much more dynamic behaviors can be obtained by using the NSFD scheme than those in the forward Euler scheme. These confirmed results can at least guarantee true available numerical results to investigate complex neuron dynamical systems.
-
-
References
[1] E. M. Adamu, K. C. Patidar and A. Ramanantoanina, An unconditionally stable nonstandard finite difference method to solve a mathematical model describing Visceral Leishmaniasis, Math. Comput. Simul., 2021, 187(12), 171-190. [2] H. Al-Kahby, F. Dannan and S. Elaydi, Non-standard Discretization Methods for Some Biological Models, World Scientific, Singapore, 2000. [3] M. Biswas and N. Bairagi, On the dynamic consistency of a two-species competitive discrete system with toxicity: Local and global analysis, J. Comput. Appl. Math., 2020, 363, 145-155. doi: 10.1016/j.cam.2019.06.005 [4] S. Chen, C. Cheng and Y. Lin, Application of a two-dimensional hindmarsh-rose type model for bifurcation analysis, Int. J. Bifurcation Chaos, 2013, 23(3), 50055. [5] Q. A. Dang and M. T. Hoang, Numerical dynamics of nonstandard finite difference schemes for a computer virus propagation model, Int. J. Dyn. Control., 2020, 8(3), 772-778. doi: 10.1007/s40435-019-00604-y [6] D. T. Dimitrov and H. V. Kojouharov, Nonstandard finite-difference methods for predator-prey models with general functional response, Math. Comput. Simul., 2008, 78(1), 1-11. doi: 10.1016/j.matcom.2007.05.001 [7] C. C. Felicio and P. C. Rech, Arnold tongues and the Devil's staircase in a discrete-time Hindmarsh-Rose neuron model, Phys. Lett. A., 2015, 379(43-44), 2845-2847. [8] J. Guckenheimer and P. Holmes, Nonlinear oscillations, dynamical systems, and bifurcations of vector fields, Springer, New York, 1983. [9] W. Kahan and R. Li, Unconventional Schemes for a Class of Ordinary Differential Equations-With Applications to the Korteweg-de Vries Equation, J. Comput. Phys., 1997, 134(2), 316-331. doi: 10.1006/jcph.1997.5710 [10] V. A. Kumar, R. M. Kumar and C. Carlo, A numerical scheme for a class of generalized Burgers' equation based on Haar wavelet nonstandard finite difference method, Appl. Numerical Math., 2021, 168, 41-54. doi: 10.1016/j.apnum.2021.05.019 [11] A. P. Kuznetsov and Y. V. Sedova, The simplest map with three-frequency quasi-periodicity and quasi-periodic bifurcations, Int. J. Bifurcation Chaos, 2016, 26(8), 1630019. doi: 10.1142/S0218127416300196 [12] Y. A. Kuznetsov, Elements of applied bifurcation theory, Second Edition, Springer, New York, 1999. [13] B. Li and Q. He, Bifurcation analysis of a two-dimensional discrete Hindmarsh-Rose type model, Adv. Differ. Equ., 2019, 2019(1), 1-17. doi: 10.1186/s13662-018-1939-6 [14] B. Li and Z. He, Bifurcations and chaos in a two-dimensional discrete Hindmarsh-Rose model, Nonlinear Dyn., 2014, 76(1), 697-715. doi: 10.1007/s11071-013-1161-8 [15] R. E. Mickens, Nonstandard Finite Difference Models of Differential Equations, World Scientific, Singapore, 1993. [16] S. M. Moghadas, M. E. Alexander and B. D. Corbett, A non-standard numerical scheme for a generalized Gause-type predator-prey model, Phys. D., 2004, 188(1), 134-151. [17] M. Namjoo, M. Zeinadini and S. Zibaei, Nonstandard finite-difference scheme to approximate the generalized Burgers-Fisher equation, Math. Meth. Appl. Sci., 2018, 41(17), 8212-8228. doi: 10.1002/mma.5283 [18] E. Ott, Chaos in dynamical systems, Cambridge University Press, Cambridge, UK, 1993. [19] L. I. W. Roeger, Nonstandard finite-difference schemes for the Lotka-Volterra systems: generalization of Mickens's method, J. Differ. Equ. Appl., 2006, 12(9), 937-948. doi: 10.1080/10236190600909380 [20] L. I. W. Roeger and G. Lahodny, Dynamically consistent discrete Lotka-Volterra competition systems, J. Differ. Equ. Appl., 2013, 19(2), 191-200. doi: 10.1080/10236198.2011.621894 [21] L. I. W. Roeger, Local Stability of Euler's and Kahan's Methods, J. Differ. Equ. Appl., 2004, 10(6), 601-614. doi: 10.1080/10236190410001659723 [22] S. Tsuji, T. Ueta, H. Kawakami, H. Fujii and K. Aihara, Bifurcations in two-dimensional Hindmarsh-Rose type model, Int. J. Bifurcation Chaos, 2007, 17(3), 985-998. doi: 10.1142/S0218127407017707 [23] H. Wang, Y. Zheng and Q. Lu, Stability and bifurcation analysis in the coupled HR neurons with delayed synaptic connection, Nonlinear Dyn., 2017, 88(3), 2091-2100. doi: 10.1007/s11071-017-3364-x [24] S. Wiggins, Introduction to applied nonlinear dynamical systems and chaos, Springer, New York, 1990. [25] Y. Yu and H. Cao, Integral step size makes a difference to bifurcations of a discrete-time Hindmarsh-Rose model, Int. J. Bifurcation Chaos, 2015, 25(2), 1550029. -
-
Figures(5) / Tables(1)
Export File
Citation
Yue Li, Hongjun Cao. BIFURCATION AND COMPARISON OF A DISCRETE-TIME HINDMARSH-ROSE MODEL[J]. Journal of Applied Analysis & Computation, 2023, 13(1): 34-56. doi: 10.11948/20210204
Format
Content
DownLoad:
-
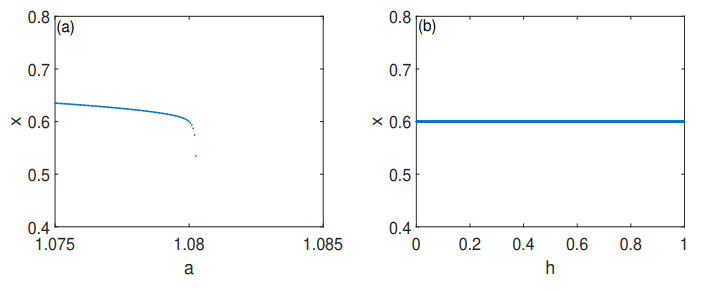
Figure 1.
(a) Bifurcation diagram of model (1.3) in
$ (a, x) $ $ b=5, c=1, d = 2, h=0.1 $ $ (0.6, 0.528) $ $ (h, x) $ $ a=1.080, b=5, c=1, d = 2 $ $ (0.6, 0.528) $ -
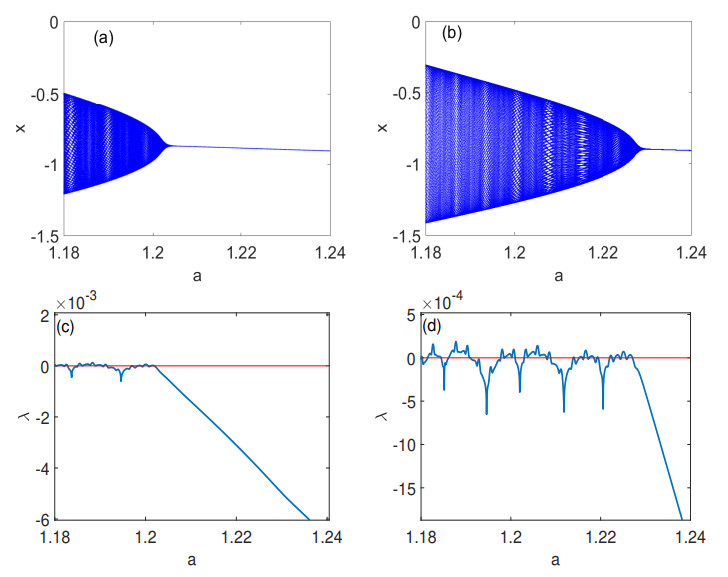
Figure 2.
(a) Neimark-Sacker bifurcation diagram of model (1.3) in
$ (a, x) $ $ b=1, c=2, d = 3, h=0.1 $ $ (- 0.8, -0.6) $ $ (a, x) $ $ b=1, c=2, d = 3, h=0.1 $ $ (- 0.8, -0.6) $ -
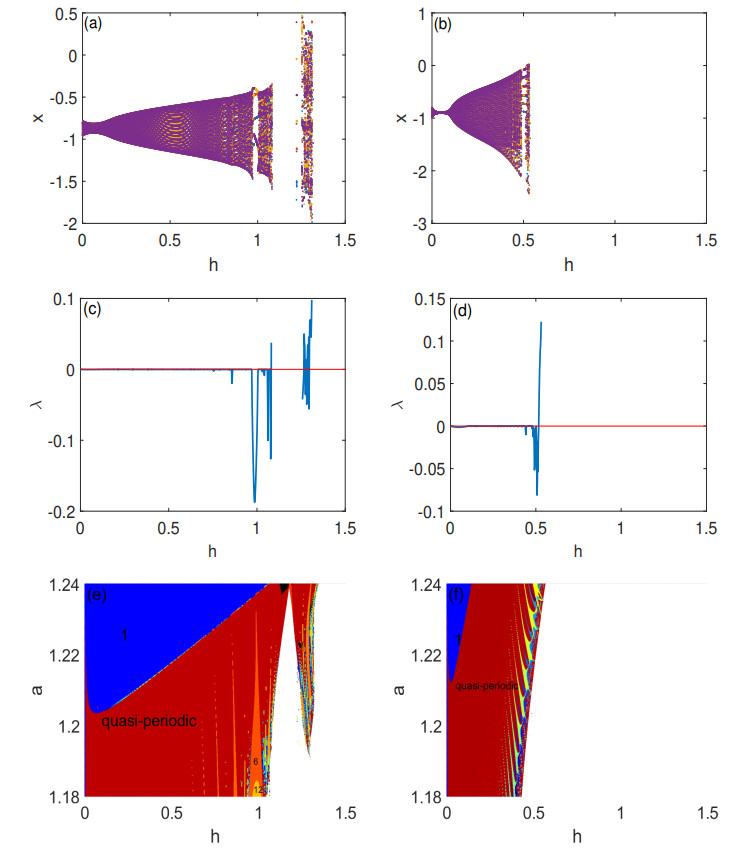
Figure 3.
(a) Neimark-Sacker bifurcation diagram of model (1.3) in
$ (h, x) $ $ a=1.2023, b=1, c=2, d = 3 $ $ (- 0.8, -0.6) $ $ (h, x) $ $ a=1.2277, b=1, c=2, d = 3 $ $ (- 0.8, -0.6) $ $ (h, a) $ $ (h, a) $ -
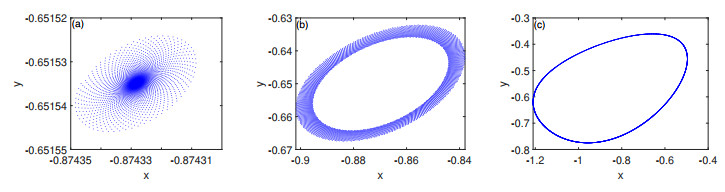
Figure 4.
Phase portraits for various values of
$ a $ $ a=1.207 $ $ a=1.20235 $ $ a=1.18 $ -
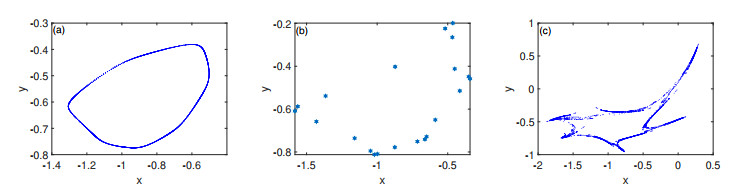
Figure 5.
Phase portraits for various values of
$ h $ $ h=0.855 $ $ h=1.081 $ $ h=1.299 $ $ 0.06967 $