| Citation: | Yuanheng Wang, Xueting Li, Bingnan Jiang. TWO NEW INERTIAL RELAXED GRADIENT CQ ALGORITHMS ON THE SPLIT EQUALITY PROBLEM[J]. Journal of Applied Analysis & Computation, 2022, 12(1): 436-454. doi: 10.11948/20210351 |
TWO NEW INERTIAL RELAXED GRADIENT CQ ALGORITHMS ON THE SPLIT EQUALITY PROBLEM
-
Abstract
In order to better solve the split equality problems in Hilbert spaces, we propose two new algorithms. Combining inertial iteration methods, we construct an inertial simultaneous relaxed gradient CQ algorithm with adaptive step size, and prove its weak convergence under simpler and more straightforward conditions. Combining viscous iteration in the above algorithm, we construct an inertial viscosity simultaneous relaxed gradient CQ algorithm, and prove the strong convergence of the algorithm under simpler and more straightforward conditions. We also give some numerical experiments to compare with some known algorithms, which demonstrate the rationality and superiority of our algorithms in several rates of convergence.
-

-
References
[1] C. Byrne, A unified treatment of some iterative algorithms in signal processing and image reconstraction, Inverse Probl., 2004, 20(1), 103-120. doi: 10.1088/0266-5611/20/1/006 [2] L. Ceng, Q. H. Ansari and J. Yao, Some iterative methods for finding fixed points and for solving constrained convex minimization problems, Nonlinear Anal., 2011, 74(16), 5286-5302. doi: 10.1016/j.na.2011.05.005 [3] Y. Censor and T. Elfving, A multiprojection algorithm using Bregman projections in a product space, Numer. Algor., 1994, 8(2), 221-239. doi: 10.1007/BF02142692 [4] P. Cholamjiak, S. Suantai and P. Sunthrayuth, Stong convergence of a general viscosity explicit rule for the sum of two monotone operators in Hilbert spaces, J. Appl. Anal. Comput., 2019, 9(6), 2137-2155. [5] J. Fan, L. Liu and X. Qin, A subgradient extragradient algorithm with inertial effects for solving strongly pseudomonotone variational inequalities, Optimization, 2020, 69(9), 2199-2215. doi: 10.1080/02331934.2019.1625355 [6] B. Jiang, Y. Wang and J. Yao, Multi-step inertial regularized methods for hierarchical variational inequality problems involving generalized Lipschitzian mappings, Mathematics, 2021, 9(17), Article ID 2103. [7] K. R. Kazmi, R. Ali and M. Furkan, Common solution to a split equality monotone variational inclusion problem, a split equality generalized general variational-like inequality problem and a split equality fixed point problem, Fixed Point Theory, 2019, 20(1), 211-231. doi: 10.24193/fpt-ro.2019.1.14 [8] S. Kesornporm, N. Pholasa and P. Cholamjiak, On the convergenece analysis of the gradient-CQ algorithms for the split feasibility problem, Numner. Algor., 2020, 84(3), 997-1017. doi: 10.1007/s11075-019-00790-y [9] L Lin and W. Takahashi, A general iterative method for hierarchical variational inequality problems in Hilbert spaces and applications, Positivity, 2012, 16(3), 429-453. doi: 10.1007/s11117-012-0161-0 [10] R. Meštrović and D. Kalaj, A converse of Minkowski's type inequalities, J. Inequal. Appl., 2010, 2010, Article ID 461215. [11] A. Moudafi, A relaxed alternating CQ-algorithm for convex feasibility problems, Nonlinear Anal., 2013, 79, 117-121. doi: 10.1016/j.na.2012.11.013 [12] E. U. Ofoedu and N. N. Araka, Simultaneous approximation methods for common solution of equilibrium, fixed point and split equality problems, J. Nonlinear Convex Anal., 2019, 20(1), 85-101. [13] C. Pan and Y. Wang, Convergence theorems for modified inertial viscosity splitting methods in Banach spaces, Mathematics, 2019, 7(2), Article ID 156. [14] L. Shi, R. Chen and Y. Wu, Strong convergence of iterative algorithms for the split equality problem, J. Inequal. Appl., 2014, 2014, Article ID 478. [15] R. Shukla and R. Pant, Approximating solution of split equality and equilibrium problems by viscosity approximation algorithms, Comput. Appl. Math., 2018, 37(4), 5293-5314. doi: 10.1007/s40314-018-0637-z [16] B. Tan, Z. Zhou and X. Qin, Accelerated projection-based forward-backward splitting algorithms for monotone inclusion problems, J. Appl. Anal. Comput., 2020, 10(5), 2184-2197. [17] D. Tian and L. Jiang, Two-step methods and relaxed two-step methods for solving the split equality problem, Comput. Appl. Math., 2021, 40(3), Article ID 83. [18] Y. Wang, C. Li and L. Lu, A new algorithm for the common solutions of a generalized variational inequality system and a nonlinear operator equation in Banach spaces, Mathematics, 2020, 8(11), Article ID 1944. [19] Y. Wang and C. Pan, Viscosity approximation methods for a general variational inequality system and fixed point problems in Banach spaces, Symmetry, 2020, 12(1), Article ID 36. [20] H. Xu, Iterative methods for the split feasibility problem in infinite-dimensional Hilbert space, Inverse Probl., 2010, 26(10), Article ID 105018. -
-
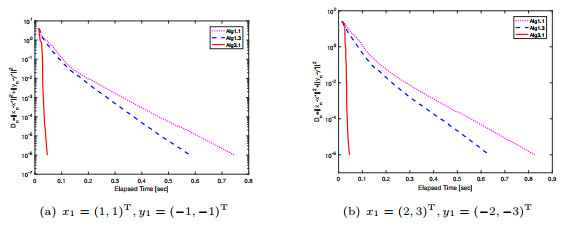
- Figure 1. The error versus the elapsed time of Algorithm 1.1, Algorithm 1.3 and Algorithm 3.1 for Example 5.1
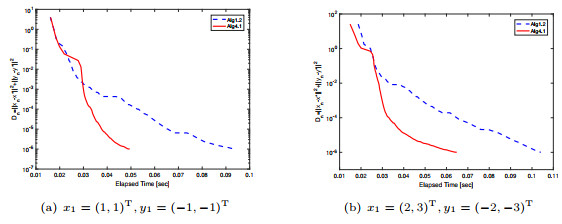
- Figure 2. The error versus the elapsed time of Algorithm 1.2 and Algorithm 4.1 for Example 5.1




 DownLoad:
DownLoad: