| Citation: | Pengfei Song, Yanni Xiao. ESTIMATING TIME-VARYING REPRODUCTION NUMBER BY DEEP LEARNING TECHNIQUES[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 1077-1089. doi: 10.11948/20220136 |
ESTIMATING TIME-VARYING REPRODUCTION NUMBER BY DEEP LEARNING TECHNIQUES
-
Abstract
Estimating time-varying reproduction number $ \mathcal{R}_{t} $ is important for quantifying the transmission ability, capturing the trend of infectious disease and assessing the effectiveness of public health intervention measures. However, accurate estimation of $ \mathcal{R}_{t} $ remains a challenging work. Deep neural networks are uniform approximators and have an unreasonable and counterintuitive effectiveness in learning unknown functions, thus can be applied to represent $ \mathcal{R}_{t} $. In this paper, we will estimate $ \mathcal{R}_{t} $ by universal differential equation method which embeds neural network $ \mathcal{R}_{t} $ into a differential equation. Compared with other methods such as state space, EpiEstim and EpiNow2 methods, deep learning method can achieve better performance with fewer data sources.
-

-
References
[1] S. Abbott, J. Hellewell, R. N. Thompson et al., Estimating the time-varying reproduction number of SARS-CoV-2 using national and subnational case counts, Wellcome Open Research, 2020, 5(112), 112. [2] R. M. Anderson and R. M. May, Infectious Diseases of Humans: Dynamics and Control, Cambridge University Press, 1991. [3] A. G. Baydin, B. A. Pearlmutter, A. A. Radul and J. M. Siskind, Automatic Differentiation in Machine Learning: A Survey, J Mach Learn Res, 2018, 18. [4] Y. Bengio, J. Louradour, R. Collobert and J. Weston, Curriculum learning, in Proceedings of the 26th Annual International Conference on Machine Learning - ICML '09, ACM Press, Montreal, Quebec, Canada, 2009, 1–8. [5] J. Bezanson, A. Edelman, S. Karpinski and V. B. Shah, Julia: A fresh approach to numerical computing, SIAM review, 2017, 59(1), 65–98. doi: 10.1137/141000671 [6] S. L. Brunton, J. L. Proctor and J. N. Kutz, Discovering governing equations from data by sparse identification of nonlinear dynamical systems, Proc. Natl. Acad. Sci. U.S.A., 2016, 113(15), 3932–3937. doi: 10.1073/pnas.1517384113 [7] Y. Cao, S. Li, L. Petzold and R. Serban, Adjoint Sensitivity Analysis for Differential-Algebraic Equations: The Adjoint DAE System and Its Numerical Solution, SIAM J. Sci. Comput., 2003, 24(3), 1076–1089. doi: 10.1137/S1064827501380630 [8] B. Chang, M. Chen, E. Haber and E. H. Chi, AntisymmetricRNN: A Dynamical System View on Recurrent Neural Networks, arXiv preprint arXiv: 1902.09689, 2019. [9] T. Q. Chen, Y. Rubanova, J. Bettencourt and D. K. Duvenaud, Neural Ordinary Differential Equations, in NeurIPS, 2018. [10] X. Chen, Ordinary differential equations for deep learning, arXiv preprint arXiv: 1911.00502, 2019. [11] N. Chopin, O. Papaspiliopoulos et al., An introduction to sequential Monte Carlo, Springer, 2020. [12] A. Cori, N. M. Ferguson, C. Fraser and S. Cauchemez, A new framework and software to estimate time-varying reproduction numbers during epidemics, Am. J. Epidemiol., 2013, 178(9), 1505–1512. doi: 10.1093/aje/kwt133 [13] M. Cranmer, A. Sanchez-Gonzalez, P. Battaglia et al., Discovering Symbolic Models from Deep Learning with Inductive Biases, ArXiv200611287 Astro-Ph Physicsphysics Stat, 2020. [14] R. Dandekar, K. Chung, V. Dixit et al., Bayesian Neural Ordinary Differential Equations, ArXiv201207244 Cs, 2021. [15] A. Davies, P. Veličković, L. Buesing et al., Advancing mathematics by guiding human intuition with AI, Nature, 2021, 600(7887), 70–74. doi: 10.1038/s41586-021-04086-x [16] E. De Brouwer, J. Simm, A. Arany and Y. Moreau, GRU-ODE-Bayes: Continuous Modeling of Sporadically-Observed Time Series, ArXiv190512374 Cs Stat, 2019. [17] J. Devlin, M. -W. Chang, K. Lee and K. Toutanova, Bert: Pre-Training of Deep Bidirectional Transformers for Language Understanding, arXiv preprint arXiv: 1810.04805, 2018. [18] O. Diekmann and J. A. P. Heesterbeek, Mathematical Epidemiology of Infectious Diseases, John Wiley and Sons Ltd, Chichester, New York, 2000. [19] O. Diekmann, J. A. P. Heesterbeek and M. G. Roberts, The construction of next-generation matrices for compartmental epidemic models, J. R. Soc. Interface, 2010, 7(47), 873–885. doi: 10.1098/rsif.2009.0386 [20] S. R. Dubey, S. K. Singh and B. B. Chaudhuri, A Comprehensive Survey and Performance Analysis of Activation Functions in Deep Learning, ArXiv210914545 Cs, 2021. [21] Y. Gal and Z. Ghahramani, Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning, ArXiv150602142 Cs Stat, 2016. [22] I. Goodfellow, Y. Bengio and A. Courville, Deep Learning, MIT press, 2016. [23] K. M. Gostic, L. McGough, E. B. Baskerville et al., Practical Considerations for Measuring the Effective Reproductive Number, Rt, PLoS Comput. Biol., 2020, 16(12), e1008409. doi: 10.1371/journal.pcbi.1008409 [24] K. He, X. Zhang, S. Ren and J. Sun, Deep residual learning for image recognition, in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, 770–778. [25] K. Hornik, M. Stinchcombe and H. White, Universal approximation of an unknown mapping and its derivatives using multilayer feedforward networks, Neural Networks, 1990, 3(5), 551–560. doi: 10.1016/0893-6080(90)90005-6 [26] R. J. Hyndman and G. Athanasopoulos, Forecasting: principles and practice, OTexts, 2018. [27] W. O. Kermack and A. G. McKendrick, A contribution to the mathematical theory of epidemics, Proceedings of the Royal Society of London. Series A, Containing papers of a mathematical and physical character, 1927, 115(772), 700–721. [28] A. J. Kucharski, T. W. Russell, C. Diamond et al., Early dynamics of transmission and control of COVID-19: A mathematical modelling study, Lancet Infect. Dis., 2020, 20(5), 553–558. doi: 10.1016/S1473-3099(20)30144-4 [29] Y. LeCun, Y. Bengio and G. Hinton, Deep learning, Nature, 2015, 521(7553), 436–444. doi: 10.1038/nature14539 [30] Y. Lu, A. Zhong, Q. Li and B. Dong, Beyond finite layer neural networks: Bridging deep architectures and numerical differential equations, in International Conference on Machine Learning, PMLR, 2018, 3276–3285. [31] B. F. Maier and D. Brockmann, Effective containment explains subexponential growth in recent confirmed COVID-19 cases in China, Science, 2020. [32] C. Mingard, G. Valle-Pérez, J. Skalse and A. A. Louis, Is SGD a bayesian sampler? well, almost, Journal of Machine Learning Research, 2021, 22. [33] M. Y. Niu, L. Horesh and I. Chuang, Recurrent neural networks in the eye of differential equations, ArXiv, 2019. [34] K. V. Parag, Improved estimation of time-varying reproduction numbers at low case incidence and between epidemic waves, PLoS Comput. Biol., 2021, 17(9), e1009347. doi: 10.1371/journal.pcbi.1009347 [35] A. Pinkus, Approximation theory of the MLP model in neural networks, Acta Numer., 1999, 8, 143–195. doi: 10.1017/S0962492900002919 [36] C. Rackauckas, Y. Ma, J. Martensen et al., Universal Differential Equations for Scientific Machine Learning, Preprint, In Review, 2020. [37] Y. Rubanova, R. T. Q. Chen and D. Duvenaud, Latent ODEs for irregularly sampled time series, ArXiv, 2019. [38] L. Ruthotto and E. Haber, Deep Neural Networks Motivated by Partial Differential Equations, J Math Imaging Vis, 2020, 62(3), 352–364. doi: 10.1007/s10851-019-00903-1 [39] T. J. Sejnowski, The unreasonable effectiveness of deep learning in artificial intelligence, Proc. Natl. Acad. Sci. U.S.A., 2020, 117(48), 30033–30038. doi: 10.1073/pnas.1907373117 [40] J. Sooknanan and N. Mays, Harnessing social media in the modelling of pandemics-challenges and opportunities, Bull. Math. Biol., 2021, 83(5), 57. doi: 10.1007/s11538-021-00895-3 [41] R. N. Thompson, J. E. Stockwin, R. D. van Gaalen et al., Improved inference of time-varying reproduction numbers during infectious disease outbreaks, Epidemics, 2019, 29, 100356. doi: 10.1016/j.epidem.2019.100356 [42] J. Wallinga and P. Teunis, Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures, Am. J. Epidemiol., 2004, 160(6), 509–516. doi: 10.1093/aje/kwh255 -
-
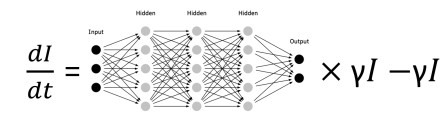
- Figure 1. Scheme of deep neural network method.
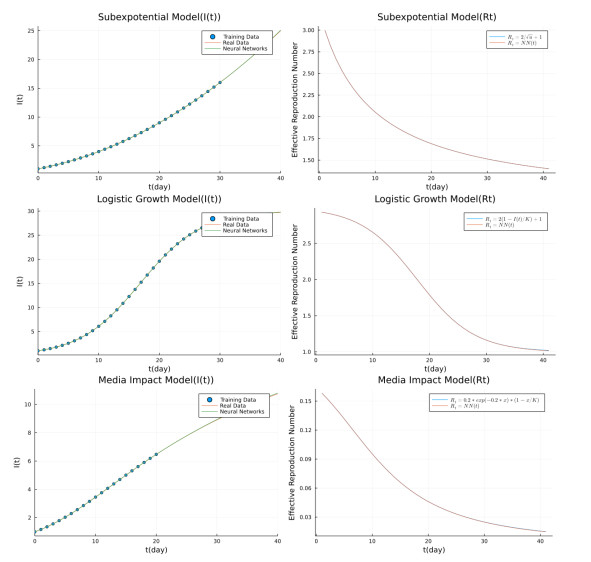
- Figure 2. Left: fitting and predicting the toy models' generating data by universal differential equations model (1.2). Right: comparing real and trained effective reproduction numbers.
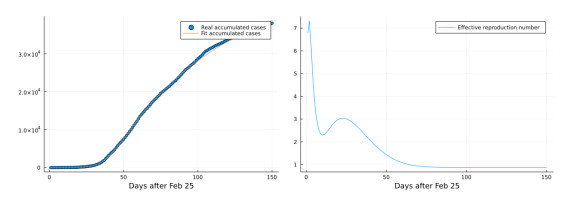
- Figure 3. Left: Ontario's first wave COVID-19 case data fit by model (1.2). Right: effective reproduction number estimation by deep learning method.
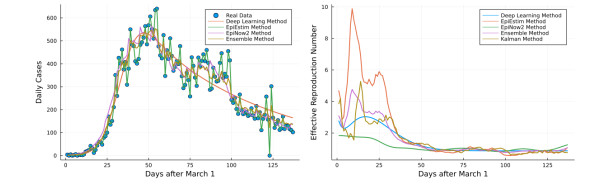
- Figure 4. Left: Ontario's first wave COVID-19 case data fit by different methods. Right: effective reproduction number estimation by different methods.




 DownLoad:
DownLoad: