| Citation: |
Wenjing Zhang, Chathuri T. Sandamali. MODELING AND ANALYSIS OF LOW-LEVEL TRANSMISSION ZIKV DYNAMICS VIA A POISSON POINT PROCESS ON SEXUAL TRANSMISSION ROUTE[J]. Journal of Applied Analysis & Computation, 2023, 13(2): 1044-1069. doi: 10.11948/20220351
|
MODELING AND ANALYSIS OF LOW-LEVEL TRANSMISSION ZIKV DYNAMICS VIA A POISSON POINT PROCESS ON SEXUAL TRANSMISSION ROUTE
-
Abstract
In this project, we modeled the low-level ZIKV transmission that was reported in Thailand [
31 ]. The secondary sexual transmission route is modeled by a Poisson point process, which leads to an increasing and saturating contact rate. This nonlinear contact rate further induces backward and Hopf bifurcations. Oscillations bifurcating from the Hopf bifurcation demonstrate the low-level persistent ZIKV transmission with sharp outbreaks, which further show varying amplitudes and frequency by considering stochastic variations on the sexual transmission rate. Global stability analysis of the disease-free equilibrium drives the disease elimination criteria for models considering vector transmission route only and considering both vector and sexual transmission routes. Bifurcation analyses prove the existence of forward and backward bifurcations, saddle-node bifurcation, and Bogdanov-Takens analytically, and further suggest the occurrence of cusp, Hopf, and general Hopf bifurcations numerically. One and two-dimensional bifurcation diagrams demonstrate the analytical results under the influence of both vector and sexual transmission rates. Sensitivity analysis suggests that an increase in mosquito death rate has the largest effect on the basic reproduction number, and an increase in human recovery rate has the most influence on decreasing human host prevalence. -
-
References
[1] A. T. Aborode, M. Sukaina, H. Kumar et al., Zika virus endemic challenges during COVID-19 pandemic in Africa, Tropical Medicine and Health, 2021, 49(1), 1-4. doi: 10.1186/s41182-020-00291-y [2] F. Agusto, S. Bewick and W. Fagan, Mathematical model for Zika virus dynamics with sexual transmission route, Ecological Complexity, 2017, 29, 61-81. doi: 10.1016/j.ecocom.2016.12.007 [3] L. Allen, An introduction to stochastic processes with applications to biology, CRC Press, Boca Raton, Fl., 2010. [4] D. Baud, D. J. Gubler, B. Schaub et al., An update on Zika virus infection, The Lancet, 2017, 390(10107), 2099-2109. doi: 10.1016/S0140-6736(17)31450-2 [5] S. Bilal and E. Michael, Effects of complexity and seasonality on backward bifurcation in vector-host models, Royal Society Open Science, 2018, 5(2), 171971. doi: 10.1098/rsos.171971 [6] S. K. Biswas, U. Ghosh and S. Sarkar, Mathematical model of Zika virus dynamics with vector control and sensitivity analysis, Infectious Disease Modelling, 2020, 5, 23-41. doi: 10.1016/j.idm.2019.12.001 [7] V. M. Cao Lormeau, A. Blake, S. Mons et al., Guillain-Barré syndrome outbreak associated with Zika virus infection in French Polynesia: a case-control study, The Lancet, 2016, 387(10027), 1531-1539. doi: 10.1016/S0140-6736(16)00562-6 [8] V. M. Cao Lormeau and D. Musso, Emerging arboviruses in the Pacific, The Lancet, 2014, 384(9954), 1571-1572. doi: 10.1016/S0140-6736(14)61977-2 [9] CDC, Mosquito control in a community, Centers for Disease Control and Prevention, 2020. [10] N. Chitnis, J. M. Hyman and J. M. Cushing, Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model, Bulletin of Mathematical Biology, 2008, 70(5), 1272. doi: 10.1007/s11538-008-9299-0 [11] D. A. Cummings, S. Iamsirithaworn, J. T. Lessler et al., The impact of the demographic transition on dengue in Thailand: insights from a statistical analysis and mathematical modeling, PLoS Medicine, 2009, 6(9), e1000139. doi: 10.1371/journal.pmed.1000139 [12] M. R. Duffy, T. -H. Chen, W. T. Hancock et al., Zika virus outbreak on Yap Island, federated states of Micronesia, New England Journal of Medicine, 2009, 360(24), 2536-2543. doi: 10.1056/NEJMoa0805715 [13] A. Enfissi, J. Codrington, J. Roosblad et al., Zika virus genome from the Americas, The Lancet, 2016, 387(10015), 227-228. doi: 10.1016/S0140-6736(16)00003-9 [14] N. M. Ferguson, Z. M. Cucunubá, I. Dorigatti et al., Countering the Zika epidemic in Latin America, Science, 2016, 353(6297), 353-354. doi: 10.1126/science.aag0219 [15] D. Gao, Y. Lou, D. He et al., Prevention and control of Zika as a mosquito-borne and sexually transmitted disease: a mathematical modeling analysis, Scientific Reports, 2016, 6(1), 28070. doi: 10.1038/srep28070 [16] N. K. Goswami, A. K. Srivastav, M. Ghosh and B. Shanmukha, Mathematical modeling of Zika virus disease with nonlinear incidence and optimal control, in Journal of Physics: Conference Series, 1000, IOP Publishing, 2018, 012114. [17] A. B. Gumel, Causes of backward bifurcations in some epidemiological models, Journal of Mathematical Analysis and Applications, 2012, 395(1), 355-365. doi: 10.1016/j.jmaa.2012.04.077 [18] J. Ikejezie, C. N. Shapiro, J. Kim et al., Zika virus transmission—region of the Americas, May 15, 2015-December 15, 2016, MMWR. Morbidity and Mortality Weekly Report, 2017, 66(12), 329. doi: 10.15585/mmwr.mm6612a4 [19] M. Kama, M. Aubry, T. Naivalu et al., Sustained low-level transmission of Zika and chikungunya viruses after emergence in the Fiji Islands, Emerging Infectious Diseases, 2019, 25(8), 1535. doi: 10.3201/eid2508.180524 [20] J. Kamtchum Tatuene, B. L. Makepeace, L. Benjamin et al., The potential role of Wolbachia in controlling the transmission of emerging human arboviral infections, Current Opinion in Infectious Diseases, 2017, 30(1), 108. doi: 10.1097/QCO.0000000000000342 [21] W. O. Kermack and A. G. McKendrick, A contribution to the mathematical theory of epidemics, Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 1927, 115(772), 700-721. doi: 10.1098/rspa.1927.0118 [22] Y. A. Kuznetsov, Elements of applied bifurcation theory, 112, Springer Science & Business Media, 2013. [23] J. Lessler, L. H. Chaisson, L. M. Kucirka et al., Assessing the global threat from Zika virus, Science, 2016, 353(6300), aaf8160. doi: 10.1126/science.aaf8160 [24] G. H. Li and Y. X. Zhang, Dynamic behaviors of a modified SIR model in epidemic diseases using nonlinear incidence and recovery rates, PLoS One, 2017, 12(4), e0175789. doi: 10.1371/journal.pone.0175789 [25] M. Lozier, L. Adams, M. F. Febo et al., Incidence of Zika virus disease by age and sex—Puerto Rico, November 1, 2015-October 20, 2016, Morbidity and Mortality Weekly Report, 2016, 65(44), 1219-1223. doi: 10.15585/mmwr.mm6544a4 [26] J. Mlakar, M. Korva, N. Tul et al., Zika virus associated with microcephaly, New England Journal of Medicine, 2016, 374(10), 951-958. doi: 10.1056/NEJMoa1600651 [27] C. Nutt and P. Adams, Zika in Africa—the invisible epidemic?, The Lancet, 2017, 389(10079), 1595-1596. doi: 10.1016/S0140-6736(17)31051-6 [28] Á. G. Pérez, E. Avila-Vales and G. E. García-Almeida, Bifurcation analysis of an SIR model with logistic growth, nonlinear incidence, and saturated treatment, Complexity, 2019. DOI: 10.1155/2019/9876013. [29] T. C. Pierson and M. S. Diamond, The emergence of Zika virus and its new clinical syndromes, Nature, 2018, 560(7720), 573-581. doi: 10.1038/s41586-018-0446-y [30] M. Roberts and J. Heesterbeek, A new method for estimating the effort required to control an infectious disease, Proceedings of the Royal Society of London. Series B: Biological Sciences, 2003, 270(1522), 1359-1364. doi: 10.1098/rspb.2003.2339 [31] K. Ruchusatsawat, P. Wongjaroen, A. Posanacharoen et al., Long-term circulation of Zika virus in Thailand: an observational study, The Lancet Infectious Diseases, 2019, 19(4), 439-446. doi: 10.1016/S1473-3099(18)30718-7 [32] C. Saad-Roy, J. Ma and P. van den Driessche, The effect of sexual transmission on Zika virus dynamics, Journal of Mathematical Biology, 2018, 77(6-7), 1917-1941. doi: 10.1007/s00285-018-1230-1 [33] Z. Shuai, J. Heesterbeek and P. van Den Driessche, Extending the type reproduction number to infectious disease control targeting contacts between types, Journal of Mathematical Biology, 2013, 67(5), 1067-1082. doi: 10.1007/s00285-012-0579-9 [34] Z. Shuai and P. van den Driessche, Global stability of infectious disease models using Lyapunov functions, SIAM Journal on Applied Mathematics, 2013, 73(4), 1513-1532. doi: 10.1137/120876642 [35] V. Sikka, V. K. Chattu, R. K. Popli et al., The emergence of Zika virus as a global health security threat: a review and a consensus statement of the INDUSEM Joint Working Group (JWG), Journal of Global Infectious Diseases, 2016, 8(1), 3. doi: 10.4103/0974-777X.176140 [36] P. Suparit, A. Wiratsudakul and C. Modchang, A mathematical model for Zika virus transmission dynamics with a time-dependent mosquito biting rate, Theoretical Biology and Medical Modelling, 2018, 15(1), 11. doi: 10.1186/s12976-018-0083-z [37] D. Taylor, Mathematical model of Zika virus transmission and control measures, The North Carolina Journal of Mathematics and Statistics, 2021, 7(1), 1-12. [38] H. R. Thieme, Mathematics in population biology, 12, Princeton University Press, 2018. [39] P. van den Driessche and J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Mathematical Biosciences, 2002, 180(1), 29 - 48. [40] J. Wang, S. Liu, B. Zheng and Y. Takeuchi, Qualitative and bifurcation analysis using an SIR model with a saturated treatment function, Mathematical and Computer Modelling, 2012, 55(3-4), 710-722. doi: 10.1016/j.mcm.2011.08.045 [41] W. Zhang, Modeling and analysis of the multiannual Cholera outbreaks with host-pathogen encounters, International Journal of Bifurcation and Chaos, 2020, 30(08), 2050120. doi: 10.1142/S0218127420501205 [42] W. Zhang, Deterministic and stochastic in-host tuberculosis models for bacterium-directed and host-directed therapy combination, Mathematical Medicine and Biology: A Journal of the IMA, 2022, 39(2), 126-155. doi: 10.1093/imammb/dqac001 [43] W. Zhang and P. Yu, Revealing the role of the effector-regulatory T cell loop on autoimmune disease symptoms via nonlinear analysis, Communications in Nonlinear Science and Numerical Simulation, 2021, 93, 105529. doi: 10.1016/j.cnsns.2020.105529 -
-
Figures(4) / Tables(1)
Export File
Citation
Wenjing Zhang, Chathuri T. Sandamali. MODELING AND ANALYSIS OF LOW-LEVEL TRANSMISSION ZIKV DYNAMICS VIA A POISSON POINT PROCESS ON SEXUAL TRANSMISSION ROUTE[J]. Journal of Applied Analysis & Computation, 2023, 13(2): 1044-1069. doi: 10.11948/20220351
Format
Content
DownLoad:
-
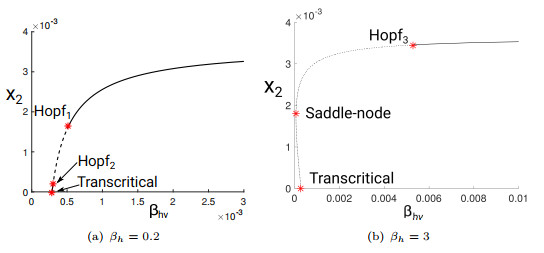
Figure 1.
Two-dimensional bifurcation diagrams.
-
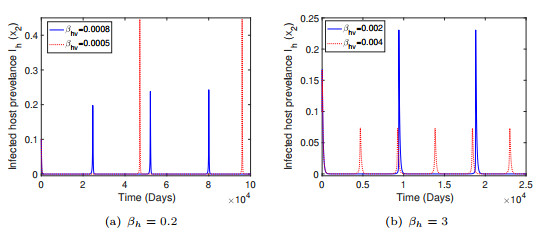
Figure 2.
One-dimensional bifurcation diagrams.
-
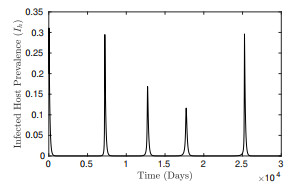
Figure 3.
Simulated low-level ZIKV transmission with uniform outbreaks
-
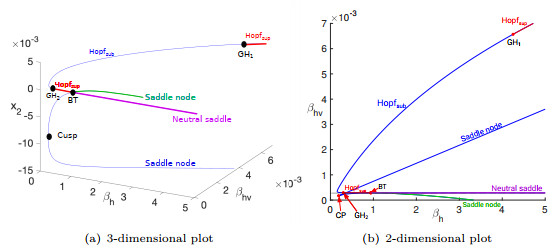
Figure 4.
Low-level ZIKV transmission with varied outbreak periods and amplitude.