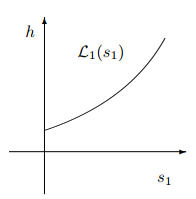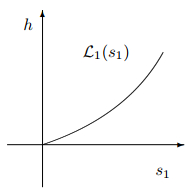| Citation: | Yinlai Jin, Dongmei Zhang, Ningning Wang, Deming Zhu. BIFURCATIONS OF TWISTED FINE HETEROCLINIC LOOP FOR HIGH-DIMENSIONAL SYSTEMS[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 2906-2921. doi: 10.11948/20230052 |
BIFURCATIONS OF TWISTED FINE HETEROCLINIC LOOP FOR HIGH-DIMENSIONAL SYSTEMS
-
Abstract
In the paper, under twisted conditions, we consider the bifurcation problem of the fine heteroclinic loop with two hyperbolic critical points for high-dimensional systems. By using the foundational solutions of the linear variational equation of the unperturbed system along the heteroclinic orbits as the local coordinate system in the small tubular neighborhood of the heteroclinic loop, we construct the Poincaré maps and obtain the bifurcation equations. Then, by considering the small nonnegative solutions of the bifurcation equations, we get the main results of the reservation of the heteroclinic orbits, the existence and existence regions, the coexistence and coexistence regions of the 1-homoclinic loop, 1-periodic orbit, 2-homoclinic loop and 2-periodic orbit. Moreover, the bifurcation surfaces and graphs are given.
-
Keywords:
- Twist /
- fine /
- heteroclinic loop /
- bifurcation /
- high-dimensional system
-

-
References
[1] V. I. Arnold, Geometric Methods in the Theory of Ordinary Differential Equations, Second Edition, Springer-Verlag, New York, 1983. [2] Y. Bai and X. Liu, Bifurcations of double homoclinic loops in reversible systems, International Journal of Bifurcation and Chaos, 2020, 30(16), 13. https://doi.org/10.1142/S0218127420502466. doi: 10.1142/S0218127420502466 [3] R. Benterki and J. Llibre, Periodic solutions of a class of Duffing differential equations, Journal of Nonlinear Modeling and Analysis, 2019, 1(2), 167–177. [4] S. N. Chow and J. K. Hale, Methods of Bifurcation Theory, Springer-Verlag, New York, 1982. [5] B. Deng, Numerical method for homoclinic and heteroclinic orbits of neuron models, Journal of Nonlinear Modeling and Analysis, 2019, 1(1), 27–45. [6] G. Deng and D. Zhu, Codimension-3 bifurcations of a class of homoclinic loop with saddle-point, Nonlinear Analysis, 2008, 69(12), 3761–3773. [7] H. Dong, T. Zhang and X. Liu, Bifurcations of double heterodimensional cycles with three saddle points, Journal of Applied Analysis & Computation, 2022, 12(6), 2143–2162. [8] Y. Fu and J. Li. Bifurcations of travelling wave solutions in three modified Camassa-Holm equations, Journal of Applied Analysis & Computation, 2021, 11(2), 1051–1061. [9] F. Geng, D. Liu and D. Zhu, Bifurcations of generic heteroclinic loop accompanied by transcritical bifurcation, International Journal of Bifurcation and Chaos, 2008, 18(4), 1069–1083. doi: 10.1142/S0218127408020847 [10] F. Geng, X. Lin and X. Liu, Chaotic traveling wave solutions in coupled chua's circuits, Journal of Dynamics and Differential Equations, 2019, 31, 1373–1396. doi: 10.1007/s10884-017-9631-1 [11] M. Han and D. Zhu, Bifurcation Theory of Differential Equations, Coal Industry Press, Beijing, 1994. [12] Q. Jia, W. Zhang, Q. Lu and X. Li, Bifurcations of double homoclinic loops with inclination flip and nonresonant eigenvalues, Journal of Nonlinear Modeling and Analysis, 2020, 2(1), 25–44. [13] Y. Jin and D. Zhu, Degenerated homoclinic bifurcations with higher dimensions, Chinese Annals of Mathematics, Series B, 2000, 21(2), 201–210. doi: 10.1142/S0252959900000224 [14] Y. Jin and D. Zhu, Bifurcations of rough heteroclinic loops with three saddles points, Acta Mathematica Sinica, English Series, 2002, 18(1), 199–208. doi: 10.1007/s101140100139 [15] Y. Jin and D. Zhu, Bifurcations of rough heteroclinic loop with two saddle points, Science in China, Series A, 2003, 46(4), 459–468. doi: 10.1007/BF02884018 [16] Y. Jin, D. Zhu and Q. Zheng, Bifurcations of rough 3-point-loop with higher dimensions, Chinese Annals of Mathematics, Series B, 2003, 24(1), 85–96. doi: 10.1142/S0252959903000098 [17] Y. Jin and D. Zhu, Twisted bifurcations and stability of homoclinic loop with higher dimensions, Applied Mathematics and Mechanics, 2004, 25(10), 1176–1183. doi: 10.1007/BF02439870 [18] Y. Jin and D. Zhu, Bifurcations of fine 3-point-loop in higher dimensional space, Acta Mathematica Sinica, English Series, 2005, 21(1), 39–52. doi: 10.1007/s10114-004-0400-9 [19] Y. Jin, F. Li and H. Xu, Bifurcations and stability of non-degenerated homoclinic loops for higher dimensional systems, Computational and Mathematical Methods in Medicine, 2013. http://dx.doi.org/10.1155/2013/582820. doi: 10.1155/2013/582820 [20] Y. Jin, X. Zhu, et al., Bifurcations of nontwisted heteroclinic loop with resonant eigenvalues, The Scientific World Journal, 2014. http://dx.doi.org/10.1155/2014/716082. doi: 10.1155/2014/716082 [21] Y. Jin, M. Zhu, et al., Bifurcations of twisted double homoclinic loops with resonant condition, The Journal of Nonlinear Science and Applications, 2016, 9(10), 5579–5620. doi: 10.22436/jnsa.009.10.08 [22] Y. Jin, S. Yang, et al., Bifurcations of heteroclininc loop with twisted conditions, International Journal of Bifurcation and Chaos, 2017, 27(8), DOI: 10.1142/S0218127417501206. [23] Y. Jin, X. Zhu, et al., Bifurcations of twisted heteroclinic loop with resonant eigenvalues, Nonlinear Dynamics, 2018, 92(2), 557–573. doi: 10.1007/s11071-018-4075-7 [24] J. Li and B. Feng, Stability, Bifurcations and Chaos, Yunnan Scientific & Technical Publishers, Kunming, 1995. doi: 10.1007/s11071-018-4075-7 [25] J. Li, Y. Zhang and J. Liang, Bifurcations and exact travelling wave solutions for a new integrable nonlocal equation, Journal of Applied Analysis & Computation, 2021, 11(3), 1588–1599. [26] J. Li and M. Han, Planar integrable nonlinear oscillators having a stable limit cycle, Journal of Applied Analysis & Computation, 2022, 12(2), 862–867. [27] X. Liu and D. Zhu, On the stability of homoclinic loop with higher dimension, Discrete and Continuous Dynamical Systems, Series B, 2012, 17(3), 915–932. doi: 10.3934/dcdsb.2012.17.915 [28] B. Long and C. Zhu. Transverse homoclinic orbit bifurcated from a homoclinic manifold by the higher order Melnikov integrals, Journal of Applied Analysis & Computation, 2020, 10(4), 1651–1665. [29] D. Luo, X. Wang, D. Zhu and M. Han, Bifurcation Theory and Methods of Dynamical Systems, World Scientific, Singapore, 1997. [30] J. Song and J. Li, Bifurcations and exact travelling wave solutions for a shallow water wave model with a non-stationary bottom surface, Journal of Applied Analysis & Computation, 2020, 10(1), 350–360. [31] Q. Tian and D. Zhu, Bifurcations of nontwisted heteroclinic loop, Science in China, 2000, 43A(8), 818–828. [32] S. Wiggins, Introduction to Applied Nonlinear Dynamical System and Chaos, Second Edition, Springer-Verleg, New York, 2003. [33] S. Wiggins, Global Bifurcations and Chaos-Analytical Methods, Springer-Verlag, New York, 1988. [34] P. Yu, M. Han and Y. Bai, Dynamics and bifurcation study on an extended Lorenz system, Journal of Nonlinear Modeling and Analysis, 2019, 1(1), 107–128. [35] L. Zhang, I. Simbanefayi and C. M. Khalique, Travelling wave solutions and conservation laws of the (2+1)-dimensional Broer-Kaup-Kupershmidt equation, Journal of Nonlinear Modeling and Analysis, 2021, 3(3), 421–430. [36] T. Zhang, T. Xu, J. Wang and Z. Jiang, Homoclinic cycle and homoclinic bifurcations of a predator-prey model with impulsive state feedback control, Journal of Nonlinear Modeling and Analysis, 2020, 2(2), 227–240. [37] T. Zhang and D. Zhu, Bifurcations of homoclinic orbit connecting two nonleading eigendirections, International Journal of Bifurcation and Chaos, 2007, 17(3), 823–836. doi: 10.1142/S0218127407017574 [38] W. Zhang and D. Zhu, Codimension 2 bifurcations of double homoclinic loops, Chaos, Solitons & Fractrals, 2009, 39(1), 295–303. [39] X. Zhang, Homoclinic, heteroclinic and periodic orbits of singularly perturbed systems, Science in China, Math., 2019, 62(9), 1687–1704. doi: 10.1007/s11425-017-9223-6 [40] D. Zhu, Problems in homoclinic bifurcation with higher dimensions, Acta Mathematica Sinica, New Series, 1998, 14(3), 341–352. [41] D. Zhu and Z. Xia, Bifurcations of heteroclinic loops, Science in China, 1998, 41A(8), 837–848. [42] D. Zhu, Exponential trichotomy and heteroclinic bifurcation, Nonlinear Analysis TMA, 1997, 28(3), 547–557. [43] D. Zhu, Melnikov vector and heteroclinic manifold, Science in China, 1994, 37A(6), 673–682. -
-
-
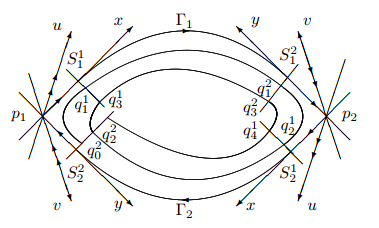
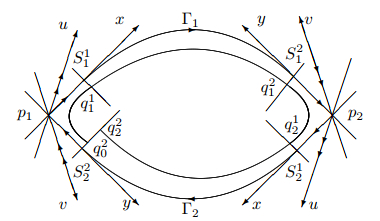
Figure 1.
Heteroclinic loop
-
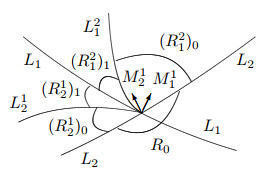
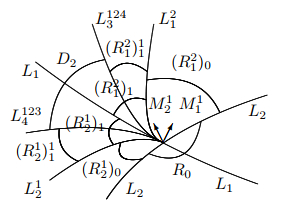
Figure 5.
$ \Delta_1=1 $ $ \Delta_2=-1 $ -
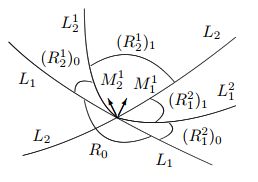
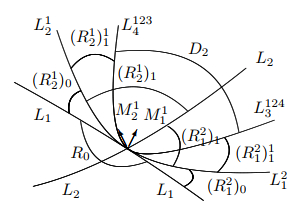
Figure 6.
$\Delta_1=-1$, $\Delta_2=1$
-
Figure 2.
$ \mu\in (R_1^2)_0 $ -
Figure 3.
$\mu\in L_1^2$ -
Figure 4.
$\mu\in (R_1^2)_1$ -
Figure 7.
Two cycle mapping
-
Figure 8.
$\Delta_1=1$ $\Delta_2=-1$ -
Figure 9.
$\Delta_1=-1$ $\Delta_2=1$ -
Figure 10.
Bifurcation graph for
$\Delta_1=1$ $\Delta_2=-1$ -
Figure 11.
Bifurcation graph for
$\Delta_1=-1$ $\Delta_2=1$




 DownLoad:
DownLoad: