| Citation: | Nguyen Thi Thu Thuy, Nguyen Trung Nghia. SOME NOVEL INERTIAL BALL-RELAXED CQ ALGORITHMS FOR SOLVING THE SPLIT FEASIBILITY PROBLEM WITH MULTIPLE OUTPUT SETS[J]. Journal of Applied Analysis & Computation, 2024, 14(3): 1485-1507. doi: 10.11948/20230259 |
SOME NOVEL INERTIAL BALL-RELAXED CQ ALGORITHMS FOR SOLVING THE SPLIT FEASIBILITY PROBLEM WITH MULTIPLE OUTPUT SETS
-
Abstract
The split feasibility problem with multiple output sets (SFPMOS) is a generalization of the well-known split feasibility problem (SFP), which has gained significant research attention due to its applications in theoretical and practical problems. However, the original CQ method for solving the SFP seems less efficient when the involved subsets are general convex sets since the method requires calculating projection onto the given sets directly. The relaxed CQ method was introduced to overcome this difficulty when the subsets are level sets of convex functions, where the projections onto the constructed half-spaces were used instead of the projections onto the original subsets. In this paper, we propose and investigate new algorithms for solving the SFPMOS when the involved subsets are given as the level sets of strongly convex functions. In this situation, we replace the half-spaces in the relaxed CQ method with balls constructed in each iteration. The algorithms are accelerated using the inertial technique and eliminate the need for calculating or estimating the norms of linear operators by employing self-adaptive step size criteria. We then analyze the strong convergence of the algorithms under some mild conditions. Some applications to the split feasibility problem are also reported. Finally, we present three numerical results, including an application to the LASSO problem with elastic net regularization, illustrating the better performance of our algorithms compared to the relevant ones.
-

-
References
[1] T. O. Alakoya, O. T. Mewomo and A. Gibali, Solving split inverse problems, Carpathian J. Math., 2023, 39(3), 583–603. [2] F. Alvarez and H. Attouch, An inertial proximal method for maximal monotone operators via discretization of a nonlinear oscillator with damping, Set-Valued Anal., 2001, 9, 3–11. doi: 10.1023/A:1011253113155 [3] H. H. Bauschke and J. M. Borwein, On projection algorithms for solving convex feasibility problems, SIAM Rev., 1996, 38, 367–426. doi: 10.1137/S0036144593251710 [4] H. H. Bauschke and P. L. Combettes, Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2011, Springer, Berlin. [5] C. Byrne, Iterative oblique projection onto convex sets and the split feasibility problem, Inverse Probl., 2002, 18, 441–453. doi: 10.1088/0266-5611/18/2/310 [6] C. Byrne, A unified treatment of some iterative algorithms in signal processing and image reconstruction, Inverse Probl., 2004, 20, 103–120. doi: 10.1088/0266-5611/20/1/006 [7] Y. Censor and T. Elfving, A multiprojection algorithm using Bregman projections in a product space, Numer. Algorithms, 1994, 8, 221–239. doi: 10.1007/BF02142692 [8] H. Cui and F. Wang, The split common fixed point problem with multiple output sets for demicontractive mappings, Optimization, 2023. DOI: 10.1080/02331934.2023.2181081. [9] T. L. Cuong, T. V. Anh and T. H. M Van, A self-adaptive step size algorithm for solving variational inequalities with the split feasibility problem with multiple output sets constraints, Numer. Funct. Anal. Optim., 2022, 43(9), 1009–1026. doi: 10.1080/01630563.2022.2071939 [10] Y. H. Dai, Fast algorithms for projection on an ellipsoid, SIAM J. Optim., 2006, 16, 986–1006. doi: 10.1137/040613305 [11] Y. Z. Dang, J. Sun and H. L. Xu, Inertial accelerated algorithms for solving a split feasibility problems, J. Ind. Manag. Optim., 2017, 13, 1383–1394. doi: 10.3934/jimo.2016078 [12] M. Fukushima, A relaxed projection method for variational inequalities, Math. Program, 1986, 35, 58–70. doi: 10.1007/BF01589441 [13] K. Goebel and S. Reich, Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings, 1984, Marcel Dekker, New York and Base. [14] S. He and C. Yang, Solving the variational inequality problem defined on intersection of finite level sets, Abstr. Appl. Anal., 2013, Article ID 942315. [15] T. Ling, X. Tong and L. Shi, Modified relaxed CQ methods for the split feasibility problems in Hilbert spaces with applications, J. Appl. Math. Comput., 2023. DOI: 10.1007/s12190-023-01875-7. [16] G. López, V. Martín-Márquez, F. Wang and H. K. Xu, Solving the split feasibility problem without prior knowledge of matrix norms, Inverse Probl., 2012, 28(8), 085004. doi: 10.1088/0266-5611/28/8/085004 [17] B. T. Polyak, Some methods of speeding up the convergence of iteration methods, USSR Comput. Math. Math. Phys., 1964, 4, 1–17. [18] S. Reich, M. T. Truong and T. N. H. Mai, The split feasibility problem with multiple output sets in Hilbert spaces, Optim. Lett., 2020, 14, 2335–2353. doi: 10.1007/s11590-020-01555-6 [19] S. Reich and T. M. Tuyen, Two new self-adaptive algorithms for solving the split common null point problem with multiple output sets in Hilbert spaces, J. Fixed Point Theory Appl., 2021, 23, 1–19. doi: 10.1007/s11784-020-00835-z [20] S. Reich and T. M. Tuyen, Regularization methods for solving the split feasibility problem with multiple output sets in Hilbert spaces, Topol. Methods Nonlinear Anal., 2022, 60(2), 547–563. [21] S. Reich and T. M. Tuyen, Two new self-adaptive algorithms for solving the split feasibility problem in Hilbert space, Numerical Algorithms, 2023. DOI: 10.1007/s11075-023-01597-8. [22] S. Reich, T. M. Tuyen, N. T. T. Thuy and M. T. N. Ha, A new self-adaptive algorithm for solving the split common fixed point problem with multiple output sets in Hilbert spaces, Numer. Algorithms, 2022, 89, 1031–1047. doi: 10.1007/s11075-021-01144-3 [23] F. Wang, The split feasibility problem with multiple output sets for demicontractive mappings, J. Optim. Theory Appl., 2022, 195(3), 837–853. doi: 10.1007/s10957-022-02096-x [24] Q. Yang, The relaxed CQ algorithm solving the split feasibility problem, Inverse Probl., 2004, 20(4), 1261–1266. doi: 10.1088/0266-5611/20/4/014 [25] H. Yu and F. Wang, A new relaxed method for the split feasibility problem in Hilbert spaces, Optimization, 2022. DOI: 10.1080/02331934.2022.2158036. [26] H. Yu, W. R. Zhan and F. H. Wang, The ball-relaxed CQ algorithms for the split feasibility problem, Optimization, 2018, 67, 1687–1699. doi: 10.1080/02331934.2018.1485677 [27] H. Zou and T. Hastie, Regularization and variable selection via the elastic net, J. R. Stat. Soc. B., 2005, 67, 301–320. doi: 10.1111/j.1467-9868.2005.00503.x -
-
-
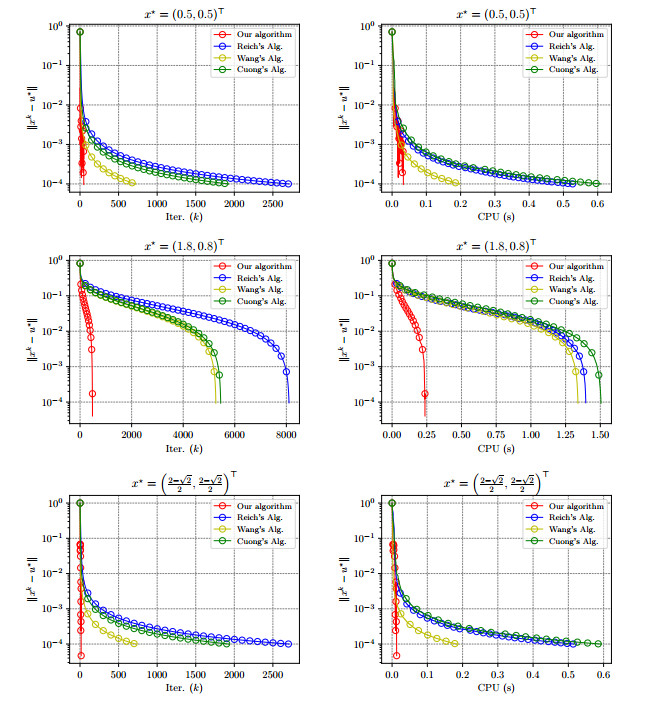
Figure 1.
The behaviors of the algorithm (1), Reich's Alg [18], Wang's Alg. [23], and Cuong's Alg. [9] in Example 5.1 with different initial guesses




 DownLoad:
DownLoad: