| Citation: |
Ali Akgül, Dumitru Baleanu, Enver Ülgül, Necibullah Sakar, Nourhane Attia. ANALYSIS OF NEW TRANSFER FUNCTIONS WITH SUM INTEGRAL TRANSFORMATION[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3282-3305. doi: 10.11948/20240001
|
ANALYSIS OF NEW TRANSFER FUNCTIONS WITH SUM INTEGRAL TRANSFORMATION
-
Abstract
We explore the novel SUM integral transform method for solving ordinary and partial differential equations, offering an effective approach beyond conventional Laplace and Sumudu transforms. Using this method, we address various differential equations, deriving transfer functions for classical and fractional derivatives. The resultant transfer functions provide valuable insights into diverse mathematical models.
-
-
References
[1] R. Agarwal and U. P. Sharma, Bicomplex Mittag-Leffler function and applications in integral transform and fractional calculus, in: P. Srivastava, M. L. Thivagar, G. I. Oros, C. C. Tan (eds) Mathematical and Computational Intelligence to Socio-Scientific Analytics and Applications. Lecture Notes in Networks and Systems, vol 518, Springer, Singapore, 2022. [2] A. Akgül, E. Ülgül, N. Sakar, B. Bilgi and A. Eker, New applications of the new general integral transform method with different fractional derivatives, Alex. Eng. J., 2023, 80, 498–505. doi: 10.1016/j.aej.2023.08.064 [3] E. K. Akgül, A. Akgül and M. Yavuz, New illustrative applications of integral transforms to financial models with different fractional derivatives, Chaos Solit. Fractals, 2021, 146, 110877. doi: 10.1016/j.chaos.2021.110877 [4] S. Q. Alasadi, A. I. M. Mansour and U. M. A. Abubakar, Applications of the SUM integral transform in science and technology: Main result, Wasit J. Eng. Sci., 2023, 2(3), 29–40. [5] M. Al-Refai and D. Baleanu, On an extension of the operator with Mittag-Leffler kernel, Fractals, 2022, 30(5), 2240129. doi: 10.1142/S0218348X22401296 [6] A. Atangana and A. Akgül, Can transfer function and Bode diagram be obtained from Sumudu transform, Alex. Eng. J., 2020, 59(4), 1971–1984. doi: 10.1016/j.aej.2019.12.028 [7] A. Atangana and D. Baleanu, New fractional derivatives with non-local and non-singular kernel: Theory and application to heat transfer model, Therm. Sci., 2016, 20(2), 763–769. doi: 10.2298/TSCI160111018A [8] D. Baleanu, A. Fernandez and A. Akgül, On a fractional operator combining proportional and classical differintegrals, Mathematics, 2020, 8(3), 360. doi: 10.3390/math8030360 [9] M. Batool, M. Farman, A. Ahmad and K. S. Nisar, Mathematical study of polycystic ovarian syndrome disease including medication treatment mechanism for infertility in women, AIMS Public Health, 2023, 11(1), 19–35. [10] M. Caputo, Linear models of dissipation whose Q is almost frequency independent–Ⅱ, Geophys. J. Int., 1967, 13(5), 529–539. doi: 10.1111/j.1365-246X.1967.tb02303.x [11] M. Caputo, A model for the fatigue in elastic materials with frequency independent Q, J. Acoust. Soc. Am., 1979, 66(1), 176–179. doi: 10.1121/1.383058 [12] M. Caputo and M. Fabrizio, A new definition of fractional derivative without singular kernel, Prog. Fract. Differ. Appl., 2015, 1(2), 73–85. [13] M. Caputo and M. Fabrizio, On the singular kernels for fractional derivatives, some applications to partial differential equations, Progr. Fract. Differ. Appl., 2021, 7(2), 79–82. doi: 10.18576/pfda/070201 [14] M. Farman, A. Shehzad, A. Akgül, E. Hincal, D. Baleanu and S. M. El Din, A fractal-fractional sex structured syphilis model with three stages of infection and loss of immunity with analysis and modeling, Results Phys., 2023, 54, 107098. doi: 10.1016/j.rinp.2023.107098 [15] S. Q. Hasan, U. M. Abubakar and M. L. Kaurangini, The new integral transform "SUM transform" and its properties, PJM, 2023, 12(1), 30–45. [16] J. Hristov, On a new approach to distributions with variable transmuting parameter: The concept and examples with emerging problems, MMNSA, 2022, 2(2), 73–87. [17] H. Jafari, A new general integral transform for solving integral equations, J. Adv. Res., 2021, 32, 133–138. [18] R. M. Jena, S. Chakraverty and M. Yavuz, Two-hybrid techniques coupled with an integral transformation for Caputo time-fractional Navier-Stokes equations, Progr. Fract. Differ. Appl., 2020, 6(3), 201–213. [19] H. S. Kadhem and S. Q. Hassan, Solving some fractional partial differential equations by invariant subspace and double Sumudu transform methods, Ibn Al-Haitham Jour. for Pure & Appl. Sci., 2020, 33(3), 127–139. [20] Kamran, S. Ahmad, K. Shah, T. Abdeljawad and B. Abdalla, On the approximation of fractal-fractional differential equations using numerical inverse Laplace transform methods, CMES, 2023, 135(3), 2743–2765. [21] M. Meddahi, H. Jafari and M. N. Ncube, New general integral transform via Atangana-Baleanu derivatives, Adv. Differ. Equ., 2021, 2021(1), 385. [22] M. Modanlıand M. E. Koksal, Laplace transform collocation method for telegraph equations defined by Caputo derivative, MMNSA, 2022, 2(3), 177–186. [23] S. Samah, M. K. Kothawade, M. Sd. Shinde and A. Maheshwari, Applicatios of Laplace transform in mechanical engineering, IRJMETS, 2022, 4(3), 1257–1264. [24] N. Sene, Second-grade fluid with Newtonian heating under Caputo fractional derivative: Analytical investigations via Laplace transforms, MMNSA, 2022, 2(1), 13–25. [25] C. Xu and M. Farman, Dynamical transmission and mathematical analysis of Ebola virus using a constant proportional operator with a power law kernel, Fractal Fract., 2023, 7(10), 706. [26] C. Xu and M. Farman, Qualitative and Ulam-Hyres stability analysis of fractional order cancer-immune model, Chaos Solit. Fractals., 2023, 177, 114277. [27] C. Xu, M. Farman and A. Shehzad, Analysis and chaotic behavior of a fish farming model with singular and non-singular kernel, Int. J. Biomath., 2023, 2350105. [28] M. Yavuz and T. Abdeljawad, Nonlinear regularized long-wave models with a new integral transformation applied to the fractional derivative with power and Mittag-Leffler kernel, Adv. Differ. Equ., 2020, 2020(1), 367. [29] M. Yavuz and N. Sene, Approximate solutions of the model describing fluid flow using generalized $\rho$-Laplace transform method and heat balance integral method, Axioms, 2020, 9(4), 123. $\rho$-Laplace transform method and heat balance integral method" target="_blank">Google Scholar
-
-
Figures(18)
Export File
Citation
Ali Akgül, Dumitru Baleanu, Enver Ülgül, Necibullah Sakar, Nourhane Attia. ANALYSIS OF NEW TRANSFER FUNCTIONS WITH SUM INTEGRAL TRANSFORMATION[J]. Journal of Applied Analysis & Computation, 2024, 14(6): 3282-3305. doi: 10.11948/20240001
Format
Content
DownLoad:
-
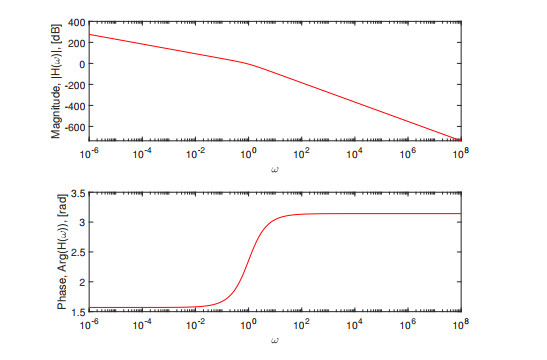
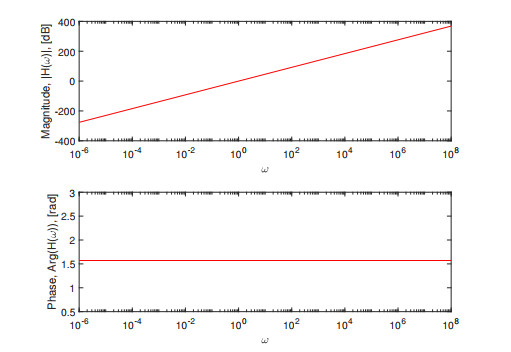
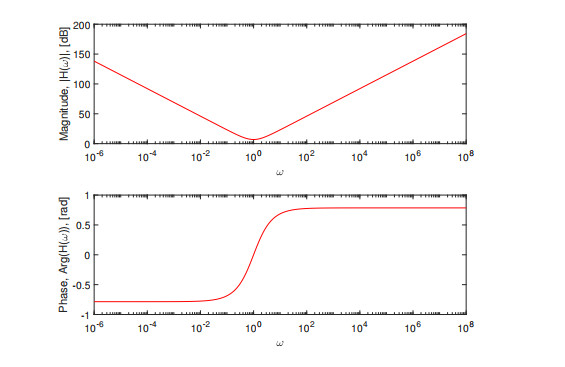
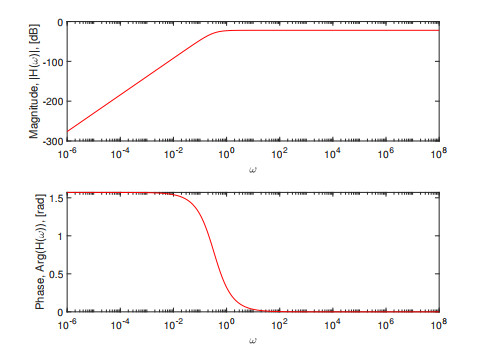
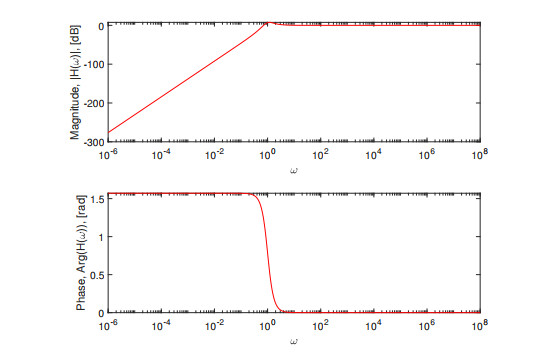
Figure 1.
SUM integral transform with the classical derivative
-
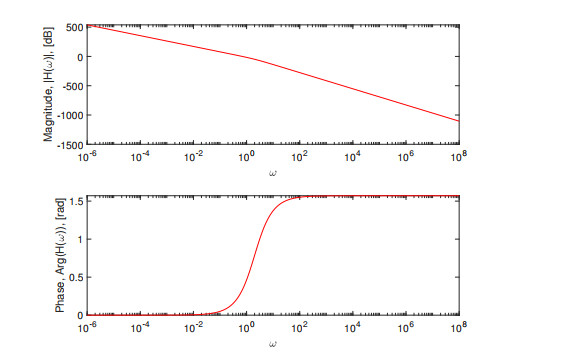
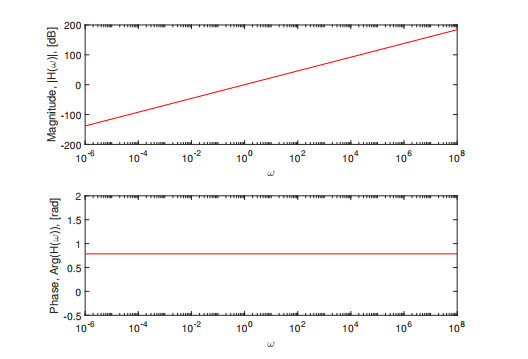
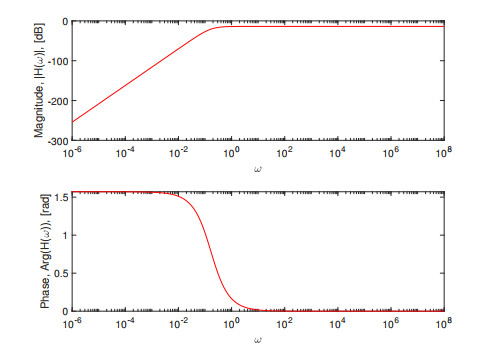
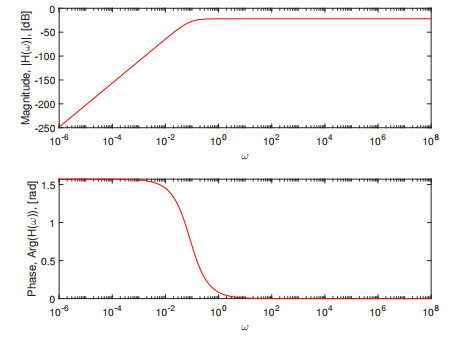
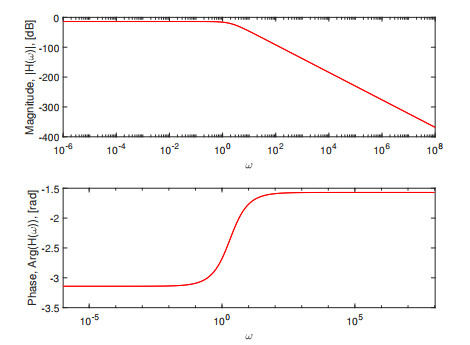
Figure 2.
SUM integral transform with the Caputo derivative
-
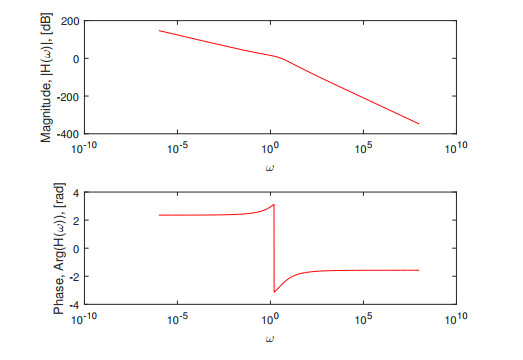
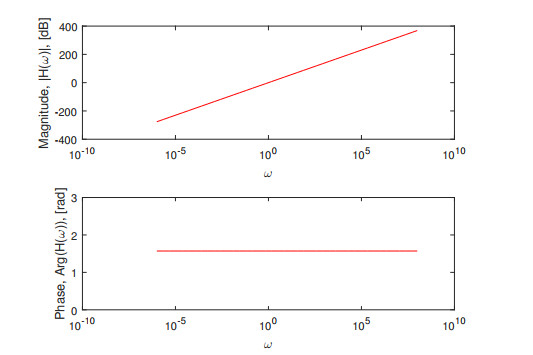
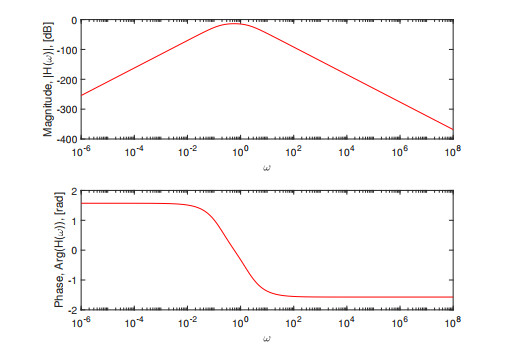
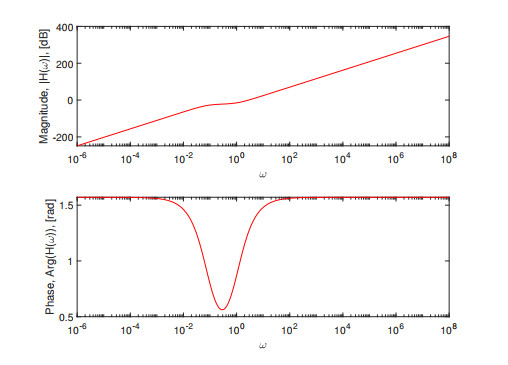
Figure 3.
SUM integral transform with the Modified Caputo-Fabrizio derivative
-
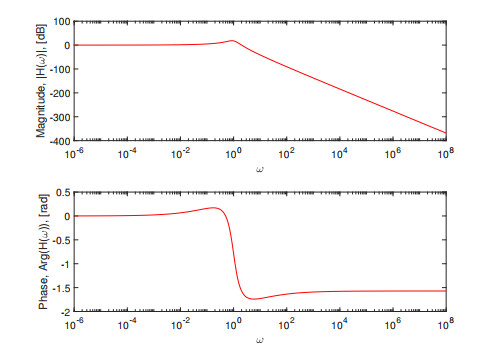
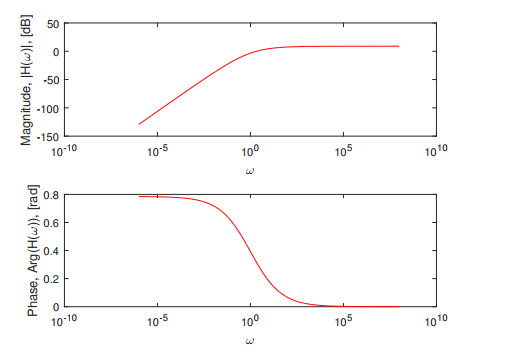
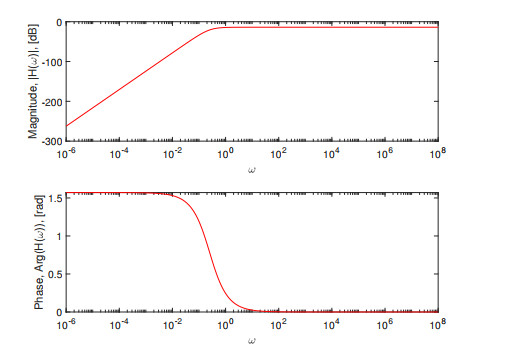
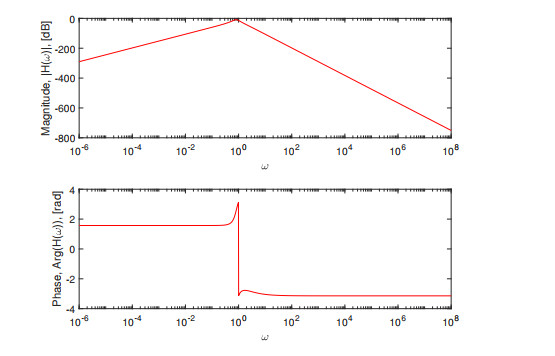
Figure 4.
SUM integral transform with the Modified Atangana-Baleanu derivative
-
Figure 5.
SUM integral transform with the Constant Proportional Caputo derivative
-
Figure 6.
Transfer function for
$ a=e $ -
Figure 7.
Transfer function for
$ \phi=0.5, a=e $ -
Figure 8.
Transfer function (4.4) for
$ \phi=1 $ $ a=e $ -
Figure 9.
Transfer function (4.5) for
$ a=e, f(0)=1, $ $ \phi=\frac{1}{2} $ -
Figure 10.
Transfer function for
$ a=e, f(0)=1, \phi=\frac{1}{2}, k_1(\phi)=1, k_0(\phi)=1 $ -
Figure 11.
Transfer function for
$ a=e, c=3, R=2 $ -
Figure 12.
Transfer function for
$ a=e, C=2, R=1, L=1 $ -
Figure 13.
Transfer function (5.8) for
$ a=e, C=2, R=2, $ $ \phi=1 $ -
Figure 14.
Transfer function (5.9) for
$ C=1, a=e, R=3, $ $ \phi=1 $ -
Figure 15.
Transfer function (5.10) for
$ C=4, a=e, R=3, $ $ \phi=1 $ -
Figure 16.
Transfer function for
$ C=4, a=e, R=3, \phi=2, k_1(\phi)=1, k_0(\phi)=1 $ -
Figure 17.
Transfer function for
$ C=3, a=e, R=2, \phi=3, k_1(\phi)=1, k_0(\phi)=1 $ -
Figure 18.
Transfer function for
$ C=3, a=e, R=2, \phi=2, k_1(\phi)=1, k_0(\phi)=1 $