| Citation: | Weipeng Zhang, Fengjie Geng, Xinyu Meng, Hongpeng Zhang. STOCHASTIC BIFURCATION ANALYSIS IN A SIV EPIDEMIC MODEL WITH POPULATION MIGRATION[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3704-3727. doi: 10.11948/20250062 |
STOCHASTIC BIFURCATION ANALYSIS IN A SIV EPIDEMIC MODEL WITH POPULATION MIGRATION
-
Abstract
In this paper, we propose a stochastic SIV epidemic model with population migration and analyze its stochastic stability and bifurcation. By utilizing polar coordinate transformation, stochastic averaging method and singular boundary theory, we prove the stochastic local and global stability of the system. Moreover, we derive sufficient conditions for the system to undergo the stochastic pitchfork bifurcation and Hopf bifurcation. Finally, numerical simulations are performed to verify the theoretical results.
-
Keywords:
- Stochastic bifurcation /
- stochastic stability /
- epidemic model /
- invariant measure
-

-
References
[1] M. E. Alexander and S. M. Moghadas, Periodicity in an epidemic model with a generalized non-linear incidence, Math. Biosci., 2004, 189(1), 75–96. doi: 10.1016/j.mbs.2004.01.003 [2] L. Arnold, Random Dynamical Systems, Springer, Berlin, 1998. [3] I. Bashkirtseva, Stochastic canards in a modified Leslie-Gower population model, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2024, 34(15), Paper No. 2450194, 11 pp. [4] S. Y. Cai, Y. M. Cai and X. R. Mao, A stochastic differential equation SIS epidemic model with two independent brownian motions, J. Math. Anal. Appl., 2019, 474(2), 1536–1550. doi: 10.1016/j.jmaa.2019.02.039 [5] S. Gao and X. Q. Sun, The global dynamics for a stochastic SIR epidemic model with vaccination, J. Nonl. Mod. Anal., 2024, 6(4), 1091–1121. [6] X. Q. He, M. Liu and X. F. Xu, Dynamic analysis of stochastic spruce budworm differential model with time delay, J. Nonl. Mod. Anal., 2022, 4(4), 677–685. [7] W. W. Hou and M. A. Han, Limit cycle bifurcations in a class of piecewise Hamiltonian systems, Commun. Nonlinear Sci. Numer. Simul., 2025, 143, Paper No. 108643, 28 pp. [8] J. C. Huang, M. Lu, C. Xiang and L. Zou, Bifurcations of codimension 4 in a Leslie-type predator-prey model with Allee effects, J. Differential Equations, 2025, 414, 201–241. doi: 10.1016/j.jde.2024.09.009 [9] Z. T. Huang, Q. G. Yang and J. F. Cao, Stochastic stability and bifurcation for the chronic state in marchuk's model with noise, Appl. Math. Model., 2011, 35(12), 5842–5855. doi: 10.1016/j.apm.2011.05.027 [10] Z. J. Kan, J. Wang, J. C. Zhang and J. C. Niu, Random P-bifurcation in a Duffing–van der Pol vibro-impact system with a Bingham model, Chaos, 2025, 35(2), Paper No. 023127, 19 pp. [11] W. O. Kermack and A. G. McKendrick, A contribution to the mathematical theory of epidemics, Proc. R. Soc. Lond. A, 1927, 115, 700–721. doi: 10.1098/rspa.1927.0118 [12] R. Z. Khasminskii, On the principle of averaging the Ito's stochastic differential equations, Kybernetika, 1968, 4, 260–279. [13] S. Kirkland, Z. S. Shuai, P. van den Driessche and X. Y. Wang, Impact of varying community networks on disease invasion, SIAM J. Appl. Math., 2021, 81(3), 1166–1189. doi: 10.1137/20M1328762 [14] Y. Kuznetsov, Elements of Applied Bifurcation Theory, Springer-Verlag, New York, 1995. [15] A. Lahrouz, T. Caraballo, I. Bouzalmat and A. Settati, Randomness suppress backward bifurcation in an epidemic model with limited medical resources, Commun. Nonlinear Sci. Numer. Simul., 2025, 140, Paper No. 108380, 17 pp. [16] G. H. Li and W. D. Wang, Bifurcation analysis of an epidemic model with nonlinear incidence, Appl. Math. Comput., 2009, 214(2), 411–423. [17] G. Lin, X. J. Wang and X. Q. Zhao, Propagation phenomena of a vector-host disease model, J. Differential Equations, 2024, 378, 757–791. [18] W. L. Liu, H. P. Zhang, W. P. Zhang and X. N. Sun, Dynamical behaviors of a tumor-immune-vitamin model with random perturbation, J. Appl. Anal. Comput., 2023, 13(5), 2739–2766. [19] Y. B. Liu, J. L. Li and D. P. Kuang, Dynamics of a stochastic SIR epidemic model with logistic growth, J. Nonl. Mod. Anal., 2023, 5(1), 73–94. [20] Y. L. Ma, Y. F. Wei, T. T. Liu and X. W. Yu, Bifurcation dynamics in a stochastic population model with Beverton-Holt growth, Appl. Math. Lett., 2024, 148, Paper No. 108892, 7 pp. [21] A. M. S. Mahdy, M. S. Mohamed, K. Lotfy, M. Alhazmi, A. A. El-Bary and M. H. Raddadi, Numerical solution and dynamical behaviors for solving fractional nonlinear rubella ailment disease model, Results Phys., 2021, 24, 104091. [22] X. R. Mao, Stochastic Differential Equations and Applications, Second Edition, Horwood Publishing, Chichester, 2008. [23] F. S. Mousavinejad, M. Fatehi Nia and A. Ebrahimi, P-bifurcation of stochastic van der Pol model as a dynamical system in neuroscience, Commun. Appl. Math. Comput., 2022, 4(4), 1293–1312. [24] N. S. Namachchivaya, Stochastic bifurcation, Appl. Math. Comput., 1990, 38, 101–159. [25] M. F. Nia and M. H. Akrami, Stability and bifurcation in a stochastic vocal folds model, Commun. Nonlinear Sci. Numer. Simul., 2019, 79, Paper No. 104898, 12 pp. [26] M. Fatehi Nia and N. Khajuee, Stability and bifurcation of stochastic chemostat model, J. Math. Model., 2023, 11(2), 375–394. [27] I. T. Nkounga, Y. Xia, S. Yanchuk, R. Yamapi and J. Kurths, Generalized FitzHugh-Nagumo model with tristable dynamics: Deterministic and stochastic bifurcations, Chaos, Solitons Fractals, 2023, 175, Paper No. 114020, 11 pp. [28] V. I. Oseledets, A multiplicative ergodic theorem: Lyapunov characteristic exponents for dynamical systems, Trans. Moscow Math. Soc., 1968, 19, 197–231. [29] J. M. Qian and L. C. Chen, Stochastic P-bifurcation analysis of a novel type of unilateral vibro-impact vibration system, Chaos Solitons Fractals, 2021, 149, Paper No. 111112, 5 pp. [30] Z. F. Shi and D. Q. Jiang, Dynamical behaviors of a stochastic HTLV-I infection model with general infection form and Ornstein–Uhlenbeck, Chaos Solitons Fractals, 2022, 165, Paper No. 112789, 15 pp. [31] X. B. Sun, Y. Tian and M. A. Han, Homoclinic bifurcation near a loop tangent to an invariant straight line, J. Differential Equations, 2025, 425, 157–189. [32] G. T. Tilahun, T. M. Tolasa, and G. A. Wole, Modeling the dynamics of rubella disease with vertical transmission, Heliyon, 2022, 8(11), Article e11797. [33] U. V. Wagner and W. V. Wedig, On the calculation of stationary solutions of multi-dimensional Fokker-Planck equations by orthogonal functions, Nonlinear Dynam., 2000, 21, 289–306. [34] M. L. Wang, Z. C. Wei, J. X. Wang, X. Yu and T. Kapitaniak, Stochastic bifurcation and chaos study for nonlinear ship rolling motion with random excitation and delayed feedback controls, Phys. D, 2024, 462, Paper No. 134147, 15 pp. [35] W. F. L. Wolfgang, H. Kliemann and N. S. Namachchivaya, Nonlinear Dynamics and Stochastic Mechanics, American Mathematical Society, 1996. [36] H. Wu, Q. B. Wang, C. Q. Zhang, Z. K. Han and R. L. Tian, Stochastic bifurcations of nonlinear vibroimpact system with time delay and fractional derivative excited by gaussian white noise, Commun. Nonlinear Sci. Numer. Simul., 2023, 124, Paper No. 107304, 15 pp. [37] X. M. Wu and S. L. Yuan, Dynamics behavior of a stochastic predator-prey model with stage structure for predator and Lévy jumps, J. Nonl. Mod. Anal., 2023, 5(2), 394–414. [38] Y. N. Xiao and S. Y. Tang, Dynamics of infection with nonlinear incidence in a simple vaccination model, Nonlinear Anal. Real World Appl., 2010, 11(5), 4154–4163. [39] H. B. Yang, X. Y. Li and W. P. Zhang, A stochastic HIV/HTLV-I co-infection model incorporating the AIDS-related cancer cells, Discrete Contin. Dyn. Syst. Ser. B, 2024, 29(2), 702–730. [40] X. F. Zhang and R. Yuan, Stochastic bifurcation and density function analysis of a stochastic logistic equation with distributed delay and weak kernel, Math. Comput. Simulation, 2022, 195, 56–70. [41] Y. H. Zhang and P. F. Song, Dynamics of the piecewise smooth epidemic model with nonlinear incidence, Chaos Solitons Fractals, 2021, 146, Paper No. 110903, 7 pp. [42] W. Q. Zhu, Nonlinear Stochastic Dynamics and Control: Hamilton Theory System Frame, Beijing Science Press, Beijing, 2003. [43] X. L. Zou, Y. T. Zheng, L. R. Zhang and J. L. Lv, Survivability and stochastic bifurcations for a stochastic Holling type Ⅱ predator-prey model, Commun. Nonlinear Sci. Numer. Simul., 2020, 83, Paper No. 105136, 20 pp. -
-
-
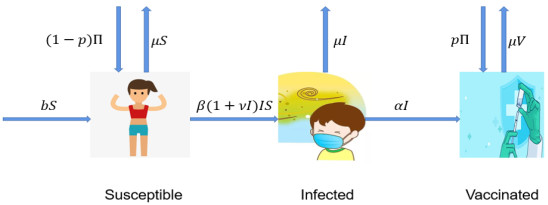
Figure 1.
Flowchart diagram of model (1.2)
-
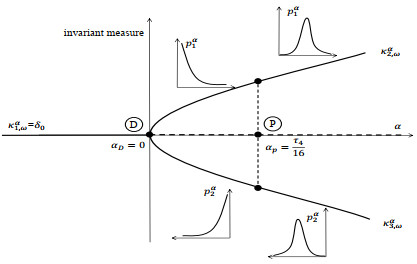
Figure 2.
Bifurcation diagram of the stochastic pitchfork bifurcation
-
Figure 3.
Phase portraits for the stable and unstable solutions of system (3.1), respectively.
-
Figure 4.
Phase portraits for system (3.1) when
$ \sigma_1=\sigma_2=0 $ -
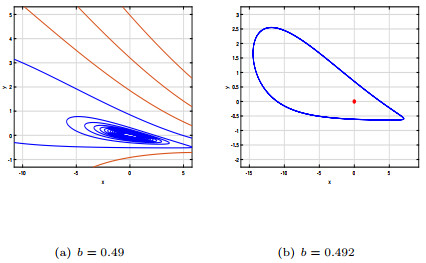
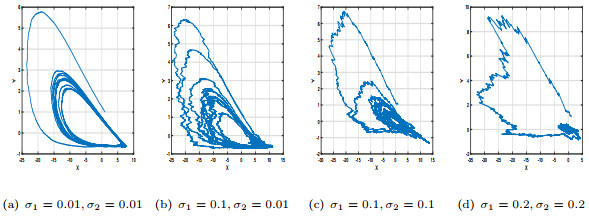
Figure 5.
For
$ b =0.49 $ -
Figure 6.
For
$ b =0.492 $ -
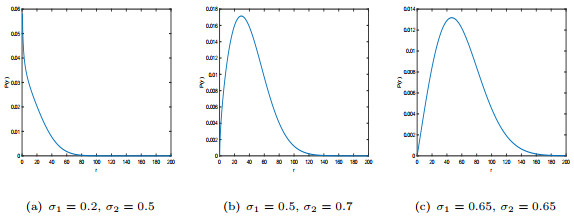
Figure 7.
The probability density function
$ P(r) $ -
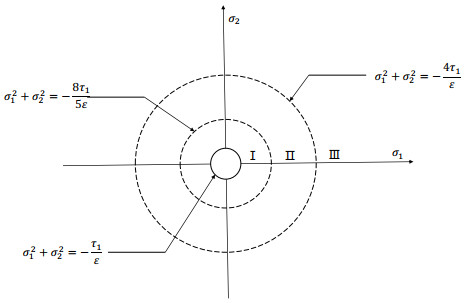
Figure 8.
The range of noise intensity of the stochastic Hopf bifurcation for system (3.6)
-
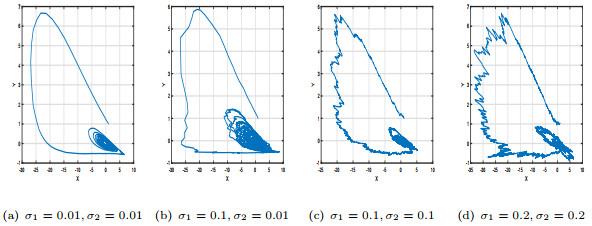
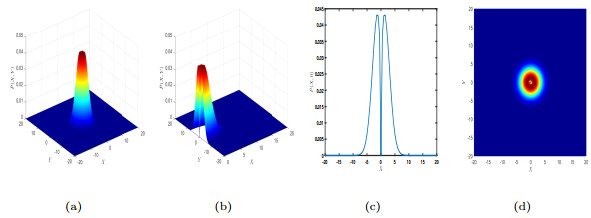
Figure 9.
In system (3.1), for
$ b=0.489 $ $ \tilde{P}(X,Y) $ $ \tilde{P}(X,Y) $ $ \tilde{P}(X,0) $ $ \tilde{P}(X,Y) $ -
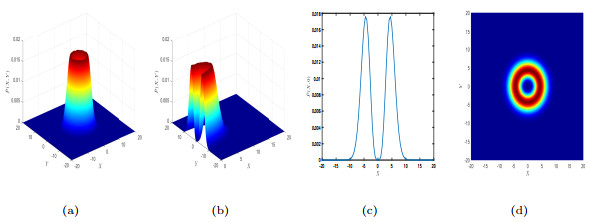
Figure 10.
In system (3.1), for
$ b=0.490 $ $ \tilde{P}(X,Y) $ $ \tilde{P}(X,Y) $ $ \tilde{P}(X,0) $ $ \tilde{P}(X,Y) $ -
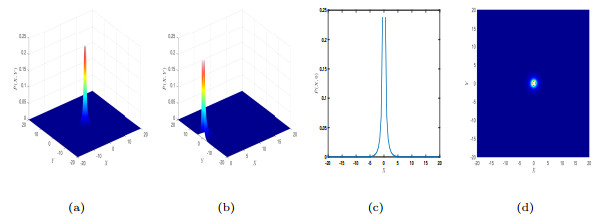
Figure 11.
In system (3.1), for
$ b=0.492 $ $ \tilde{P}(X,Y) $ $ \tilde{P}(X,Y) $ $ \tilde{P}(X,0) $ $ \tilde{P}(X,Y) $ -
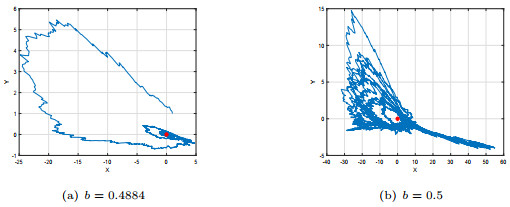
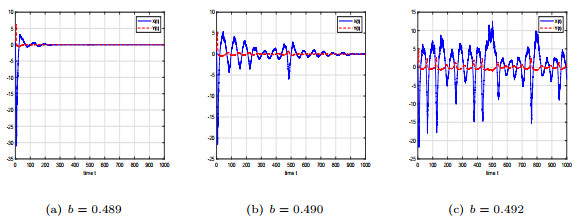
Figure 12.
The sample paths of
$ X(t) $ $ Y(t) $




 DownLoad:
DownLoad: