| Citation: | Emadidin Gahalla Mohmed Elmahdi, Jianfei Huang. A CRANK-NICOLSON L1/PI DIFFERENCE SCHEME FOR NONLINEAR TIME FRACTIONAL INTEGRO-DIFFERENTIAL EQUATION ON GRADED MESHES[J]. Journal of Applied Analysis & Computation, 2026, 16(1): 347-361. doi: 10.11948/20250119 |
A CRANK-NICOLSON L1/PI DIFFERENCE SCHEME FOR NONLINEAR TIME FRACTIONAL INTEGRO-DIFFERENTIAL EQUATION ON GRADED MESHES
-
Abstract
In this paper, a Crank-Nicolson $ L1 $/trapezoidal Product integration (PI) difference scheme is constructed to numerically solve a Volterra-type nonlinear integro-differential equation. Assuming the exact solution exhibits a weak singularity at $ t=0 $, the convergence order of the fully discrete scheme is $ \mathcal{O}\left(N^{-\min\{r\sigma, 2-\alpha, 2\}}+M^{-2}\right) $, and the stability is analyzed using an improved Gr$ \ddot{\text{o}} $nwall inequality in terms of the $ L^2 $-norm. Finally, the theoretical results are verified by numerical experiments.
-

-
References
[1] A. A. Alikhanov, P. Yadav, V. K. Singh and M. Shahbazi Asl, A high-order compact difference scheme for the multi-term time-fractional Sobolev-type convection-diffusion equation, Appl. Numer. Math., 2025, 44(115), 82–95. [2] S. Behera and S. Saha Ray, A wavelet-based novel technique for linear and nonlinear fractional Volterra-Fredholm integro-differential equations, Comput. Appl. Math., 2022, 41(1), 1–28. doi: 10.1007/s40314-021-01695-0 [3] F. Boutaous, Study of a class of fractional order non linear neutral abstract Volterra integro-differential equations with deviated arguments, Chaos Solit. Fractals, 2024, 187, 115341. doi: 10.1016/j.chaos.2024.115341 [4] Y. Cao and Z. Tan, A fast and high-order localized meshless method for fourth-order time-fractional diffusion equations, Commun. Nonlinear Sci. Numer. Simul., 2025, 142, 108586. doi: 10.1016/j.cnsns.2024.108586 [5] H. Chen and M. Stynes, Error analysis of a second-order method on fitted meshes for a time-fractional diffusion problem, J. Sci. Comput., 2019, 79(2), 624–647. [6] E. G. M. Elmahdi and J. Huang, A linearized finite difference scheme for time-space fractional non-linear diffusion-wave equations with initial singularity, Int. J. Nonlinear Sci. Numer. Simul., 2023, 24(6), 1769–1783. [7] E. G. M. Elmahdi, Y. Yi and J. Huang, Two linearized difference schemes on graded meshes for the time-space fractional nonlinear diffusion-wave equation with an initial singularity, Phys. Scr., 2025, 100(1), 015215. doi: 10.1088/1402-4896/ad95c4 [8] Y. Jiang, H. Chen, T. Sun and C. Huang, Efficient L1-ADI finite difference method for the two-dimensional nonlinear time-fractional diffusion equation, Appl. Math. Comput., 2024, 471, 128609. [9] S. Kumar, S. Das and V. K. Singh, Product integration techniques for generalized fractional integro-differential equations, Z. Angew. Math. Phys., 2025, 76(1), 1–30. doi: 10.1007/s00033-024-02358-w [10] S. Kumar and V. Gupta, An approach based on fractional-order Lagrange polynomials for the numerical approximation of fractional order nonlinear Volterra-Fredholm integro-differential equations, J. Appl. Math. Comput., 2023, 69(1), 251–272. doi: 10.1007/s12190-022-01743-w [11] H. L. Liao, W. McLean and J. Zhang, A second-order scheme with nonuniform time steps for a linear reaction-subdiffusion problem, Commun. Comput. Phys., 2021, 30(2), 567–601. doi: 10.4208/cicp.OA-2020-0124 [12] H. L. Liao, W. McLean and J. Zhang, A discrete Grönwall inequality with applications to numerical schemes for subdiffusion problems, SIAM J. Numer. Anal., 2019, 57(1), 218–237. doi: 10.1137/16M1175742 [13] S. Patnaik, J. P. Hollkamp and F. Semperlotti, Applications of variable-order fractional operators: A review, Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci., 2020, 476(2234), 20190498. [14] H. Qiao and A. Cheng, A fast finite difference method for 2D time variable fractional mobile/immobile equation, J. Appl. Math. Comput., 2024, 70(1), 551–577. doi: 10.1007/s12190-023-01973-6 [15] Y. Rostami, New technique for solving system of variable-order fractional partial integro-differential equations, Comput. Math. Phys., 2025, 65(2), 270–289. doi: 10.1134/S0965542524702063 [16] Ruby and M. Mandal, Convergence analysis and numerical implementation of projection methods for solving classical and fractional Volterra integro-differential equations, Math. Comput. Simul., 2024, 225, 889–913. doi: 10.1016/j.matcom.2023.09.015 [17] G. Saini, B. Ghosh, S. Chand and J. Mohapatra, An iterative-based difference scheme for nonlinear fractional integro-differential equations of Volterra type, Partial Differ. Equ. Appl. Math., 2025, 13, 101138. doi: 10.1016/j.padiff.2025.101138 [18] S. Santra and J. Mohapatra, Numerical analysis of volterra integro-differential equations with Caputo fractional derivative, Iran. J. Sci. Technol. Trans. Sci., 2021, 45(5), 1815–1824. doi: 10.1007/s40995-021-01180-7 [19] M. V. Shitikova, Fractional operator viscoelastic models in dynamic problems of mechanics of solids: A review, Mech. Solids, 2022, 57(5), 1–33. [20] P. Sunthrayuth, R. Ullah, A. Khan, R. Shah, J. Kafle, I. Mahariq and F. Jarad, Numerical analysis of the fractional-order nonlinear system of volterra integro-differential equations, J. Funct. Spaces, 2021, 2021, 5536569. [21] Z. Tan, Second-order non-uniform and fast two-grid finite element methods for non-linear time/fractional mobile/immobile equations with weak regularity, Appl. Math. Comput., 2025, 486, 129043. [22] S. S. Tantawy, Solving linear systems of fractional integro-differential equations by Haar and Legendre wavelets techniques, Partial Differ. Equ. Appl. Math., 2024, 10, 100683. [23] Z. Wang, L1/LDG method for Caputo-Hadamard time fractional diffusion equation, Commun. Appl. Math. Comput., 2025, 7(1), 203–227. [24] Z. Wang, D. Cen and Y. Mo, Sharp error estimate of a compact L1-ADI scheme for the two-dimensional time-fractional integro-differential equation with singular kernels, Appl. Numer Math., 2021, 159, 190–203. [25] Z. Wang and L. Sun, A numerical approximation for the Caputo-Hadamard derivative and its application in time-fractional variable-coefficient diffusion equation, Discrete Contin. Dyn. Syst., 2024, 17(6), 2679–2705. [26] Y. Yang, J. Huang and H. Li, An α-robust analysis of finite element method for space-time fractional diffusion equation, Numer. Algorithms, 2025, 98(1), 165–190. [27] F. Yu and M. Chen, Second-order error analysis for fractal mobile/immobile Allen-Cahn equation on graded meshes, J. Sci. Comput., 2023, 96(1), 49. [28] H. Zhu and C. Xu, A highly efficient numerical method for the time-fractional diffusion equation on unbounded domains, J. Sci. Comput., 2024, 99(1), 1–34. [29] L. Zou and Y. Zhang, Numerical solutions of multi-term fractional reaction-diffusion equations, AIMS Math., 2025, 10(1), 777–792. -
-
-
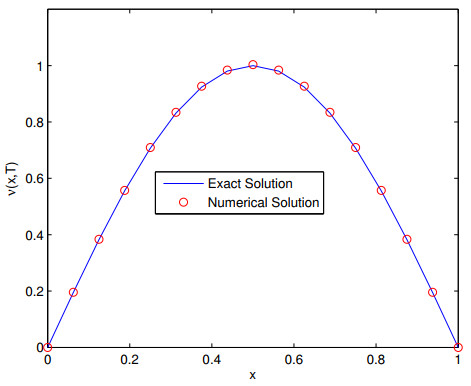
Figure 1.
The comparison between the exact solution
$ \nu(x, t) $ -
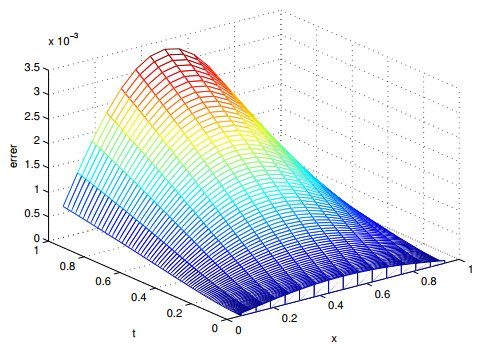
Figure 2.
The error surface between the numerical solution and the exact solution of schemes (3.5) and (3.6).




 DownLoad:
DownLoad: