| Citation: |
Yaru Fu, Xiaoyu Jiang, Zhaolin Jiang, Seongtae Jhang. INVERSES AND EIGENPAIRS OF TRIDIAGONAL TOEPLITZ MATRIX WITH OPPOSITE-BORDERED ROWS[J]. Journal of Applied Analysis & Computation, 2020, 10(4): 1599-1613. doi: 10.11948/20190287
|
INVERSES AND EIGENPAIRS OF TRIDIAGONAL TOEPLITZ MATRIX WITH OPPOSITE-BORDERED ROWS
-
Abstract
In this paper, tridiagonal Toeplitz matrix (type I, type II) with opposite-bordered rows are introduced. Main attention is paid to calculate the determinants, the inverses and the eigenpairs of these matrices. Specifically, the determinants of an $n\times n$ tridiagonal Toeplitz matrix with opposite-bordered rows can be explicitly expressed by using the $(n-1)$th Fibonacci number, the inversion of the tridiagonal Toeplitz matrix with opposite-bordered rows can also be explicitly expressed by using the Fibonacci numbers and unknown entries from the new matrix. Besides, we give the expression of eigenvalues and eigenvectors of the tridiagonal Toeplitz matrix with opposite-bordered rows. In addition, some algorithms are presented based on these theoretical results. Numerical results show that the new algorithms have much better computing efficiency than some existing algorithms studied recently.-
Keywords:
- Tridiagonal Toeplitz matrix /
- opposite-bordered /
- Fibonacci number /
- determinant /
- inverse /
- eigenpairs
-
-
References
[1] R. H. Chan and X. Jin, Circulant and skew-circulant preconditioners for skew-Hermitian type Toeplitz systems, JBIT, 1991, 31, 632-646. [2] S. Cheng, Partial difference equations, Taylor and Francis, London, 2003. [3] B. Choudhury, Diffusion of heat in multidimensional composite spherical body, IMA J. Appl. Math., 2013, 78(3), 474-493. doi: 10.1093/imamat/hxr062 [4] M. El-Mikkawy and F. Atlan, A new recursive algorithm for inverting general $k$-tridiagonal matrices, Appl. Math. Lett., 2015, 44, 34-39. doi: 10.1016/j.aml.2014.12.018 CrossRef $k$-tridiagonal matrices" target="_blank">Google Scholar
[5] M. El-Mikkawy and A. Karawia, Inversion of general tridiagonal matrices, Appl. Math. Lett., 2006, 19(8), 712-720. doi: 10.1016/j.aml.2005.11.012 [6] M. El-Shehawey, G. El-Shreef and A. Shal-Henawy, Analytical inversion of general periodic tridiagonal matrices, J. Math. Anal. Appl., 2008, 345, 123-134. [7] C. M. da Fonseca, On the eigenvalues of some tridiagonal matrices, J. Comput. Appl. Math., 2007, 200(1), 283-286. [8] C. M. da Fonseca and F. Yılmaz, Some comments on ${\rm k}$-tridiagonal matrices: Determinant, spectra and inversion, Appl. Math. Comput., 2015, 270, 644-647. ${\rm k}$-tridiagonal matrices: Determinant, spectra and inversion" target="_blank">Google Scholar
[9] C. M. da Fonseca and J. Petronilho, Explicit inverses of some tridiagonal matrices, Linear Algebra Appl., 2001, 325, 7-21. doi: 10.1016/S0024-3795(00)00289-5 [10] C. M. da Fonseca and J. Petronilho, Explicit inverse of a tridiagonal ${\rm k}$-Toeplitz matrix, Numer. Math., 2005, 100, 457-482. doi: 10.1007/s00211-005-0596-3 CrossRef ${\rm k}$-Toeplitz matrix" target="_blank">Google Scholar
[11] C. Fischer and R. Usmani, Properties of some tridiagonal matrices and their application to boundary value problems, SIAM J. Numer. Anal., 1969, 6(1), 127-142. [12] P. L. Giscard, S. J. Thwaite and D. Jaksch, Evaluating matrix functions by resummations on graphs: The method of path-sums, SIAM J. Matrix Anal. Appl., 2013, 34(2), 445-469. doi: 10.1137/120862880 [13] S. Holmgren and K. Otto, Iterative solution methods and preconditioners for non-symmetric non-diagonally dominant block-tridiagonaI systems of equations, Dept. of Computer Sci., Sweden, 1989. [14] Y. Huang and W. F. McColl, Analytical inversion of general tridiagonal matrices, J. Phys. A: Math. Gen., 1997, 30, 7919-7933. doi: 10.1088/0305-4470/30/22/026 [15] G. G. Jesús, Powers of tridiagonal matrices with constant diagonals, Appl. Math. Comput., 2008, 206, 885-891. [16] J. T. Jia, A breakdown-free algorithm for computing the determinants of periodic tridiagonal matrices, Numer. Algorithms, 2020, 83, 149-163. doi: 10.1007/s11075-019-00675-0 [17] J. Jia and S. Li, New algorithms for numerically solving a class of bordered tridiagonal systems of linear equations, Comput. Math. Appl., 2019, 78, 144-151. doi: 10.1016/j.camwa.2019.02.028 [18] J. Jia and S. Li, On the inverse and determinant of general bordered tridiagonal matrices, Comput. Math. Appl., 2015, 69, 503-509. doi: 10.1016/j.camwa.2015.01.012 [19] J. Jia and S. Li, Symbolic algorithms for the inverses of general $k$-tridiagonal matrices, Comput. Math. Appl., 2015, 70, 3032-3042. doi: 10.1016/j.camwa.2015.10.018 CrossRef $k$-tridiagonal matrices" target="_blank">Google Scholar
[20] J. Jia, T. Sogabe and M. El-Mikkawy, Inversion of $k$-tridiagonal matrices with Toeplitz structure, Comput. Math. Appl., 2013, 65, 116-125. doi: 10.1016/j.camwa.2012.11.001 CrossRef $k$-tridiagonal matrices with Toeplitz structure" target="_blank">Google Scholar
[21] Z. Jiang, X. Chen and J. Wang, The explicit inverses of CUPL-Toeplitz and CUPL-Hankel matrices, E. Asian. J. Appl. Math., 2017, 7(1), 38-54. [22] X. Jiang and K. Hong, Skew cyclic displacements and inversions of two innovative patterned matrices, Appl. Math. Comput., 2017, 308, 174-184. [23] X. Jiang, K. Hong and Z. Fu, Skew cyclic displacements and decompositions of inverse matrix for an innovative structure matrix, J. Nonlinear Sci. Appl., 2017, 10, 4058-4070. doi: 10.22436/jnsa.010.08.02 [24] Z. Jiang and D. Wang, Explicit group inverse of an innovative patterned matrix, Appl. Math. Comput., 2016, 274, 220-228. [25] R. Mattheij and M. Smooke, Estimates for the inverse of tridiagonal matrices arising in boundary-value problems, Linear Algebra Appl., 1986, 73, 33-57. doi: 10.1016/0024-3795(86)90232-6 [26] G. Meurant, A review on the inverse of symmetric tridiagonal and block tridiagonal matrices, SIAM J. Matrix Anal. Appl., 1992, 13(3), 707-728. doi: 10.1137/0613045 [27] K. H. Rosen, Discrete Mathematics and Its Applications, (sixth ed.) New York: McGraw-Hill, 2011. [28] K. Thomas. Fibonacci and Lucas Numbers with Applications, John Wiley & Sons, 2001. [29] H. Tim and K. Emrah, An analytical approach: Explicit inverses of periodic tridiagonal matrices, J. Comput. Appl. Math., 2018, 335, 207-226. doi: 10.1016/j.cam.2017.11.038 [30] R. A. Usmani, Inversion of a tridiagonal Jacobi matrix, Linear. Algebra Appl., 1994, 212(213), 413-414. [31] A. Yalçiner, The LU factorizations and determinants of the $k$-tridiagonal matrices, Asian-Eur. J. Math., 2011, 4(1), 187-197. doi: 10.1142/S1793557111000162 CrossRef $k$-tridiagonal matrices" target="_blank">Google Scholar
[32] W. C. Yueh and S. Cheng, Explicit eigenvalues and inverses of tridiagonal Toeplitz matrices with four perturbed corners, ANZIAM J., 2008, 49, 361-387. doi: 10.1017/S1446181108000102 [33] W. C. Yueh and S. Cheng, Explicit eigenvalues and inverses of several Toeplitz matrices, ANZIAM J., 2006, 48(1), 73-97. doi: 10.1017/S1446181100003424 [34] F. Zhang. The Schur Complement and Its Applications, Springer Science & Business Media, 2006. [35] Y. Zheng, S. Shon and J. Kim, Cyclic displacements and decompositions of inverse matrices for CUPL Toeplitz matrices, J. Math. Anal. Appl., 2017, 455, 727-741. doi: 10.1016/j.jmaa.2017.06.016 [36] Y. Zheng and S. Shon, Exact determinants and inverses of generalized Lucas skew circulant type matrices, Appl. Math. Comput., 2015, 270, 105-113. -
-
Figures(2) / Tables(2)
Export File
Citation
Yaru Fu, Xiaoyu Jiang, Zhaolin Jiang, Seongtae Jhang. INVERSES AND EIGENPAIRS OF TRIDIAGONAL TOEPLITZ MATRIX WITH OPPOSITE-BORDERED ROWS[J]. Journal of Applied Analysis & Computation, 2020, 10(4): 1599-1613. doi: 10.11948/20190287
Format
Content
DownLoad:
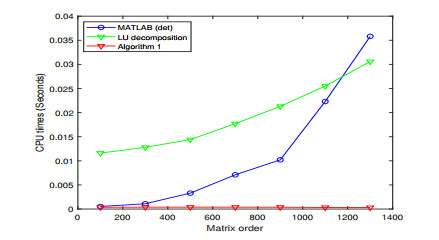
- Figure 1. The CPU times comparison of calculating the determinant.
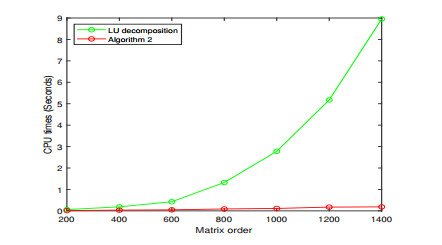
- Figure 2. The CPU times comparison of calculating the inverse.