| Citation: |
Lin Hu, Lin-Fei Nie. THE EFFECTS OF DELAY AND IMPULSIVE DRUG THERAPY IN AN HIV MODEL WITH CTLS IMMUNE RESPONSE[J]. Journal of Applied Analysis & Computation, 2021, 11(1): 333-350. doi: 10.11948/20190418
|
THE EFFECTS OF DELAY AND IMPULSIVE DRUG THERAPY IN AN HIV MODEL WITH CTLS IMMUNE RESPONSE
-
Abstract
Considering the effects of immune response and drug therapy on HIV treatment, an HIV mathematical control model with CTLs immune response is therefore proposed, where the delay of virus invasion and impulsive drug therapy are introduced. By utilizing the comparison theorem, differential inequality theories and analytic method, the threshold values for the existence and global stability of the virus-free periodic solution, and the uniform persistence of disease without CTLs immune response are studied. Numerical simulations are performed to illustrate the main theoretical results and the feasibility of drug therapy. Our theoretical results suggest that long-term and standardized medication can prolong the infection process and spread of the virus, or suppress the virus concentration below the detectable level. -
-
References
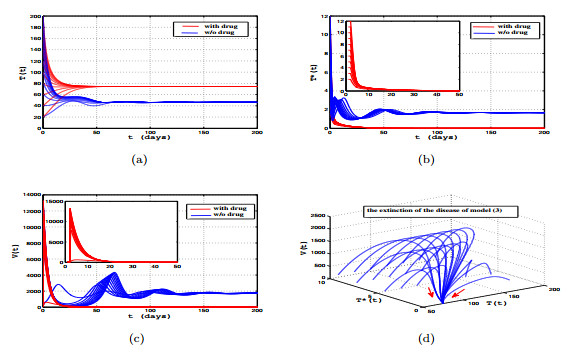
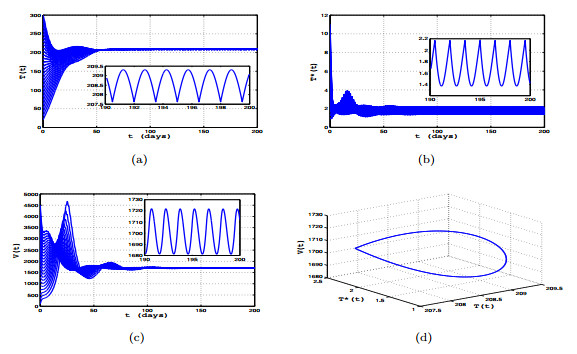
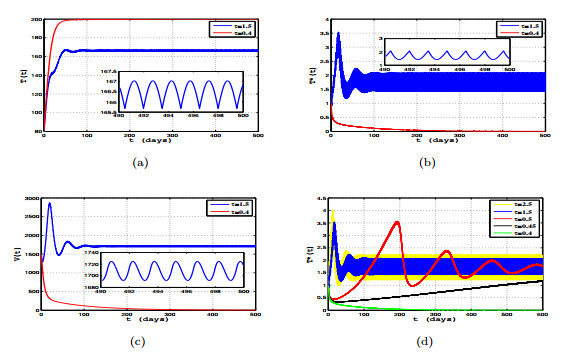
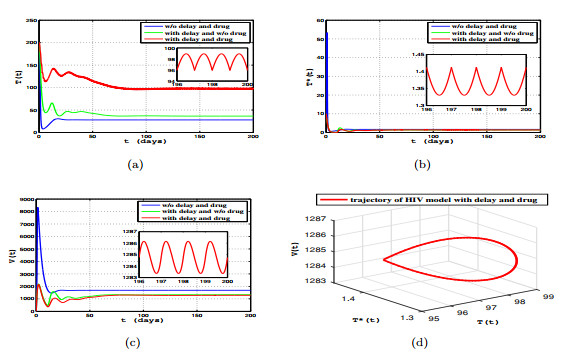
[1] P. Aavani and L.J.S. Allen, The role of CD4 T cells in immune system activation and viral reproduction in a simple model for HIV infection,Appl. Math. Model., 2019, 75, 210-222. doi: 10.1016/j.apm.2019.05.028 [2] R. Arnaout, M. Nowak and D. Wodarz, HIV-1 dynamics revisited: biphasic decay by cytotoxic lymphocyte killing? Proc. R. Soc. Lond. B., 2000, 265, 1347-1354. [3] D. Burg, L. Rong, A. U. Neumann and H. Dahari, Mathematical modeling of viral kinetics under immune control during primary HIV-1 infection,J. Theor. Biol., 2009, 259, 751-759. doi: 10.1016/j.jtbi.2009.04.010 [4] M. S. Ciupe, B. L. Bivort, D. M. Bortz and P.W. Nelson, Estimating kinetic parameters from HIV primary infection data through the eyes of three different mathematical models,Math. Biosci., 2006, 200, 1-27. doi: 10.1016/j.mbs.2005.12.006 [5] J. M. Conway and A. S. Perelson, Residual viremia in treated HIV$.+$ individuals,PLoS Comput. Biol., 2016, 12(1), e1004677. doi: 10.1371/journal.pcbi.1004677 [6] A. M. Croicu, A. M. Jarrett, N. G. Cogan and M. Y. Hussaini, Short-term antiretroviral treatment recommendations based on sensitivity analysis of a mathematical model for HIV infection of CD4(+)T cells,Bull. Math. Biol., 2017, 79(11), 2649-2671. doi: 10.1007/s11538-017-0345-7 [7] R. V. Culshaw and S. Ruan, A delay-differential equation model of HIV infection of CD$4.+$ T-cells,Math. Biosci., 2000, 165, 27-39. doi: 10.1016/S0025-5564(00)00006-7 [8] J. Danane and K. Allali, Mathematical analysis and clinical implications of an HIV Model with adaptive immunity,Comput. Math. Method Med., 2019, 2019, Article ID 7673212. [9] M. Divya and M. Pitchaimani, An analysis of the delay-dependent HIV-1 protease inhibitor model,Int. J. Biomath., 2018, 11(3), Article ID 1850031. [10] A. M. Elaiw and A. D. Al Agha, Stability of a general HIV-1 reaction-diffusion model with multiple delays and immune response,Physica A, 2019, 536(15), Article ID 122593. [11] K. Hattaf, N. Yousfi and A. Tridane, A delay virus dynamics model with general incidence rate,Differ. Equ. Dyn. Syst., 2014, 22, 181-190. doi: 10.1007/s12591-013-0167-5 [12] A. V. M. Herz, S. Bonhoeffer, R. M. Anderson, R. M. May and M. A. Nowak, Viral dynamics in vivo: Limitations on estimates of intracellular delay and virus decay,Proc. Natl. Acad. Sci. USA, 1996, 93, 7247-7251. doi: 10.1073/pnas.93.14.7247 [13] D. D. Ho, A. U. Neumann, A. S. Perelson, W. Chen, J. M. Leonard and M. Markowitz, Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection,Nature, 1995, 373, 123-126. doi: 10.1038/373123a0 [14] P. Jacqmin, L. McFadyen and J. R. Wade, Basic PK/PD principles of drug effects in circular/proliferative systems for disease modelling,J. Pharmacokinet. Pharmacodyn., 2010, 37, 157-177. doi: 10.1007/s10928-010-9151-7 [15] J. L. Katharine, P. G. Geoffrey and P. S. George, An estimate of the global prevalence and incidence of herpes simplex virus type 2 infection,Bull. World Health Organ., 2008, 86(10), 805-812. doi: 10.2471/BLT.07.046128 [16] D. E. Kirschner and G. G. Webb, Immunotherapy of HIV-1 infection,J. Biol. Syst., 1998, 6, 71-83. doi: 10.1142/S0218339098000091 [17] O. Krakovska and L. M. Wahl, Optimal drug treatment regimens for HIV depend on adherence,J. Theor. Biol., 2007, 246, 499-509. doi: 10.1016/j.jtbi.2006.12.038 [18] V. Lakshmikantham, D. D. Bainov and P. S. Simeonov, Theory of Impulsive Differential Equations,World Scientific, Singapore, 1989. [19] C. Monica and M. Pitchaimani, Geometric Stability switch criteria in HIV-1 infection delay, J. Nonlinear Sci., 2019, 29(1), 163-181. doi: 10.1007/s00332-018-9481-y [20] L. F. Nie, Z. Teng and I. H. Jung, Complex dynamic behavior in a viral model with state feedback control strategies,Nonlinear Dyn., 2014, 77, 1223-1236. doi: 10.1007/s11071-014-1372-7 [21] M. A. Nowak and C. R. Bangham, Population dynamics of immune responses to persistent virues,Science, 1996, 272, 74-79. doi: 10.1126/science.272.5258.74 [22] E. Numfor, Optimal treatment in a multi-strain within-host model of HIV with age structure,J. Math. Anal. Appl., 2019, 48(2), Article ID 123410. [23] K. S. Pawelek, S. Liu, F. Pahlevani and L. Rong, A model of HIV-1 infection with two time delays: Mathematical analysis and comparison with patient data,Math. Biosci., 2012, 235, 98-109. doi: 10.1016/j.mbs.2011.11.002 [24] A. S. Perelson, Modeling viral and immune system dynamics,Nat. Rev. Immunol., 2002, 2, 28-36. doi: 10.1038/nri700 [25] A. S. Perelson, D. Kirschner and R. De Boer, Dynamics of HIV infection of CD4$.+$T cells,Math. Biosci., 1993, 114, 81-125. doi: 10.1016/0025-5564(93)90043-A [26] A. S. Perelson and P. Nelson, Mathematical models of HIV dynamics in vivo,SIAM Review, 1999, 41, 3-44. doi: 10.1137/S0036144598335107 [27] A. S. Perelson, A. Neumann, M. Markowitz, J. Leonard and D. Ho, HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span and viral generation time,Science, 1996, 271, 1582-1586. doi: 10.1126/science.271.5255.1582 [28] A. N. Phillips, Reduction of HIV concentration during acute infection: independence from a specific immune response,Science, 1996, 271, 497-499. doi: 10.1126/science.271.5248.497 [29] L. Rong and A. S. Perelson, Asymmetric division of activated latently infected cells may explain the decay kinetics of the HIV-1 latent reservoir and intermittent viral blips,Math. Biosci., 2009, 217(1), 77-87. doi: 10.1016/j.mbs.2008.10.006 [30] N. Sachsenberg, A. S. Perelson, S. Yerly, G. A. Schockmel, D. Leduc, B. Hirschel and L. Perrin, Turnover of CD$4.+$ and CD$8.+$ T lymphocytes in HIV-1 infection as measured by ki-67 antigen,J. Exp. Med., 1998, 187, 1295-1303. doi: 10.1084/jem.187.8.1295 [31] S. Saha, P. K. Roy and R. Smith, Modeling monocyte-derived dendritic cells as a therapeutic vaccine against HIV, J. Biol. Syst., 2018, 26(4), 579-601. doi: 10.1142/S0218339018500262 [32] S. K. Sahani and Yashi, A delayed HIV infection model with apoptosis and viral loss,J. Biol. Dyn. 12(1), 2018, 1012-1034. doi: 10.1080/17513758.2018.1547427 [33] E. Shamsara, Z. Afsharnezhad and S. Effati, Optimal drug control in a four-dimensional HIV infection model,Optim. Control. Appl. Meth., 2020, 41, 469-486. doi: 10.1002/oca.2555 [34] R. J. Smith and L. M. Wahl, Distinct effects of protease and reverse transcriptase inhibition in an immunological model of HIV-1 infection with impulsive drug effects,Bull. Math. Biol., 2004, 66, 1259-1283. doi: 10.1016/j.bulm.2003.12.004 [35] R. J. Smith and L. M. Wahl, Drug resistance in an immunological model of HIV-1 infection with impulsive drug effects,Bull. Math. Biol., 2005, 67, 783–813. doi: 10.1016/j.bulm.2004.10.004 [36] Z. Teng and L. Chen, The positive periodic solutions of periodic Kolmogorov type systems with delays,Acta Math. Appl. Sci., 1999, 22, 456-464. [37] W. Wang and X. Zhao, Threshold dynamics for compartmental epidemic models in periodic environments,J. Dyn. Diff. Equat., 2008, 20, 699-717. doi: 10.1007/s10884-008-9111-8 [38] Y. Wang, Y. Zhou, F. Brauer and J. M. Heffernan, Viral dynamics model with CTL immune response incorporating antiretroviral therapy,J. Math. Biol., 2013, 67, 901-934. doi: 10.1007/s00285-012-0580-3 [39] D. Wodarz, Killer Cell Dynamics: Mathematical and Computational Approaches to Immunology,Springer, New York, 2007. [40] D. Wodarz and M. Nowak, Specific therapies could lead to long-term immunological control of HIV,Proc. Natl. Acad. Sci., 1999, 96, 464-469. [41] World health Organization, Global health sector strategy on HIV/AIDS 2011-2015,World Health Organization Press, Switzerland, 2011. [42] World health Organization main website, https://www.who.int/news-room/fact-sheets/detail/hiv-aids (accessed 15 November 2019) [43] Y. Yang and Y. Xiao, Threshold dynamics for an HIV model in periodic environments,J. Math. Anal. Appl., 2010, 361, 59-68. doi: 10.1016/j.jmaa.2009.09.012 [44] F. Zhang and X. Zhao, A periodic epidemic model in a patchy environmen,J. Math. Anal. Appl., 2007, 325, 496-516. doi: 10.1016/j.jmaa.2006.01.085 [45] X. Zhao, Dynamical Systems in Population Biology,Springer-Verlag, New York, 2003. [46] H. Zhu and X. Zou, Impact of delays in cell infection and virus production on HIV-1 dynamics,Maht. Med. Biol., 2008, 25, 99-112. [47] H. Zhu and X. Zou, Dynamics of an HIV-1 infection model with cell-mediated immune response and intracellular delay,Discrete Contin. Dyn. Syst. B, 2009, 12, 511-524. doi: 10.3934/dcdsb.2009.12.511 -
-
Figures(4) / Tables(1)
Export File
Citation
Lin Hu, Lin-Fei Nie. THE EFFECTS OF DELAY AND IMPULSIVE DRUG THERAPY IN AN HIV MODEL WITH CTLS IMMUNE RESPONSE[J]. Journal of Applied Analysis & Computation, 2021, 11(1): 333-350. doi: 10.11948/20190418
Format
Content
DownLoad:
-
Figure 1. The effect of delay and drug for HIV models (2.3) and (2.4) with
$ \lambda = 10 $ ,$ d = 0.02 $ ,$ r = 0.1 $ ,$ T_{max} $ ,$ \delta = 0.25 $ ,$ N = 1000 $ ,$ \beta = 2.5\times 10^{-5} $ ,$ c = 0.24 $ ,$ k = 1 $ ,$ \omega = 3.6 $ ,$ m = 0.36 $ ,$ p = 0.02 $ ,$ p = 0.12 $ ,$ d_E = 0.2 $ ,$ \theta = 10 $ ,$ \tau = 1 $ and the drug dosage$ D(0) = D_{in} = 10(mg) $ , where blue curves, green curves and red curves represent (2.3) and (2.4) without delay and drug therapy, with delay and without drug therapy, and with delay and drug therapy, respectively -
Figure 2. The existence and stability of the virus-free periodic solution of HIV models (2.3) and (2.4) with
$ \lambda = 1 $ ,$ d = 0.02 $ ,$ T_{max} $ ,$ \delta = 0.24 $ ,$ N = 1000 $ ,$ \beta = 2.4\times10^{-5} $ ,$ c = 0.24 $ ,$ \omega = 3.6 $ ,$ k = 1 $ ,$ m = 0.36 $ and$ \theta = 2 $ ,$ D(0) = D_{in} = 16(mg) $ and$ \tau = 0.5 $ , where the blue curves and red curves represent models (2.3) and (2.4) with drug therapy and without drug therapy, respectively -
Figure 3. The existence and stability of the endemic periodic solution of HIV models (2.3) and (2.4) with
$ \lambda = 5 $ ,$ d = 0.02 $ ,$ T_{max} = 250 $ ,$ \delta = 0.24 $ ,$ N = 1000 $ ,$ \beta = 3.6\times10^{-5} $ ,$ c = 0.24 $ ,$ k = 1 $ ,$ \omega = 3.6 $ ,$ m = 0.36 $ and$ \theta = 2 $ ,$ \tau = 1.5 $ and$ D(0) = D_{in} = 16(mg) $ -
Figure 4. The permanence and extinction of HIV models (2.3) and (2.4) with different drug therapy periodic,
$ \lambda = 4 $ ,$ d = 0.02 $ ,$ T_{max} = 200 $ ,$ \delta = 0.24 $ ,$ N = 1000 $ ,$ \beta = 2.4\times10^{-5} $ ,$ c = 0.24 $ ,$ \omega = 2.3 $ ,$ m = 0.36 $ and$ \theta = 2 $ and$ D(0) = D_{in} = 16(mg) $ , where, (a)-(c): the blue lines are$ \tau = 1.5 $ and the red lines are$ \tau = 0.4 $ ; (d)$ \tau = 2.5 $ ,$ 1.5 $ ,$ 0.5 $ ,$ 0.45 $ and$ 0.4 $ , respectively