| Citation: |
Xueqing Miao, Jiaye Gan, Tingfu Ma, Lili Wu. A LINEAR TIME-SPACE HIGH-ORDER COMPACT FINITE DIFFERENCE SCHEME FOR SOLVING THE ONE-DIMENSIONAL NONLINEAR BURGERS' EQUATION[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3226-3245. doi: 10.11948/20240527
|
A LINEAR TIME-SPACE HIGH-ORDER COMPACT FINITE DIFFERENCE SCHEME FOR SOLVING THE ONE-DIMENSIONAL NONLINEAR BURGERS' EQUATION
-
Abstract
This paper presents a novel finite difference scheme for solving the one-dimensional (1D) nonlinear Burgers' equation with high accuracy. A fourth-order backward difference formula is employed to discretize the time derivative, while the nonlinear residual terms are efficiently linearized via Taylor series expansion. Spatial discretization is achieved using a fourth-order compact difference scheme for second-order derivatives and a fourth-order Padé scheme for first-order derivatives. As a result, the proposed approach yields a linear compact finite difference scheme with fourth-order accuracy in both temporal and spatial dimensions. The accuracy and stability of this method are demonstrated through a series of numerical experiments, validating its effectiveness for solving nonlinear Burgers' equations. The high-order finite difference scheme for the nonlinear Burgers' equation can accurately simulate phenomena in fields such as physics, sound wave propagation, and aerodynamics.
-
-
References
[1] M. Abdullah, M. Yaseen and M. De la Sen, An efficient collocation method based on Hermite formula and cubic B-splines for numerical solution of the Burgers' equation, Math. Comput. Simul., 2022, 197, 166-184. doi: 10.1016/j.matcom.2022.02.013 [2] G. Arora and B. Singh, Numerical solution of Burgers' equation with modified cubic B-spline differential quadrature method, Appl. Math. Comput., 2013, 224, 166-177. [3] J. M. Burgers, A mathematical model illustrating the theory of turbulence, Adv. Appl. Mech., 1948, 1, 171-199. [4] S. A. Dahy and K. T. Elgindy, High-order numerical solution of viscous Burgers' equation using an extended Cole-Hopf barycentric Gegenbauer integral pseudospectral method, Int. J. Comput. Math., 2022, 99(3), 446-464. doi: 10.1080/00207160.2021.1919302 [5] K. T. Elgindy, High-order, stable, and efficient pseudospectral method using barycentric Gegenbauer quadratures, Appl. Numer. Math., 2017, 113, 1-25. doi: 10.1016/j.apnum.2016.10.014 [6] C. Fan and P. Li, Generalized finite difference method for solving two-dimensional Burgers' equations, Procedia Eng., 2014, 79, 55-60. doi: 10.1016/j.proeng.2014.06.310 [7] K. Fujisawa and A. Asada, Nonlinear parametric sound enhancement through different fluid layer and its application to noninvasive measurement, Meas., 2016, 94, 726-733. doi: 10.1016/j.measurement.2016.09.004 [8] I. A. Ganaie and V. K. Kukreja, Numerical solution of Burgers' equation by cubic Hermite collocation method, Appl. Math. Comput., 2014, 237, 571-581. [9] F. Gao and C. Chi, Numerical solution of nonlinear Burgers' equation using high accuracy multiquadric quasi-interpolation, Appl. Math. Comput., 2014, 229, 414-421. [10] D. A. Hammada and M. S. El-Azab, 2N order compact finite difference scheme with collocation method for solving the generalized Burger's-Huxley and Burger's-Fisher equations, Appl. Math. Comput., 2015, 258, 296-311. [11] M. Hussain, Hybrid radial basis function methods of lines for the numerical solution of viscous Burgers' equation, Comput. Appl. Math., 2021, 40(1), 1-49. doi: 10.1007/s40314-020-01383-5 [12] S. R. Jena and G. S. Gebremedhin, Decatic b-spline collocation scheme for approximate solution of Burgers' equation, Numer. Methods Partial Differ. Equ., 2023, 39, 1851-1869. doi: 10.1002/num.22747 [13] Y. D. Jin, J. Zhou, Z. K. Shi, H. L. Zhang and C. P. Wang, Lattice hydrodynamic model for traffic flow on curved road with passing, Nonlinear Dyn., 2017, 89, 107-124. doi: 10.1007/s11071-017-3439-8 [14] M. Kapoor and V. Joshi, Numerical solution of coupled 1D Burgers' equation by non-uniform algebraic-hyperbolic B-spline differential quadrature method, Int. J. Comput. Methods Eng. Sci. Mech., 2022, 24(1), 18-39. [15] A. Khoshfetrat and M. Abedini, A hybrid DQ/LMQRBF-DQ approach for numerical solution of Poisson-type and Burger's equations in irregular domain, Appl. Math. Model., 2012, 36, 1885-1901. doi: 10.1016/j.apm.2011.07.079 [16] A. Korkmaz and I. Dag, Cubic B-spline differential quadrature methods and stability for Burgers' equation, Eng. Comput., 2013, 30, 320-344. doi: 10.1108/02644401311314312 [17] S. Kutluay and Y. Ucar, Numerical solutions of the coupled Burgers equation by the Galerkin quadratic B-spline finite element method, Math. Methods Appl. Sci., 2013, 36, 2403-2415. doi: 10.1002/mma.2767 [18] H. Lai and C. Ma, A new lattice Boltzmann model for solving the coupled viscous Burgers' equation, Phys. A., 2014, 395, 445-457. doi: 10.1016/j.physa.2013.10.030 [19] S. Lele, Compact finite difference schemes with spectral-like resolution, J. Comput. Phys., 1992, 103, 16-42. doi: 10.1016/0021-9991(92)90324-R [20] P. W. Li, Space-time generalized finite difference nonlinear model for solving unsteady Burgers' equations, Appl. Math. Lett., 2021, 114, 106896. doi: 10.1016/j.aml.2020.106896 [21] M. Maryam, S. Fahimeh, B. Esmail and J. Shahnam, A local reproducing kernel method accompanied by some different edge improvement techniques: Application to the Burgers' equation, Iran. J. Sci. Technol. Trans. A Sci., 2018, 42(2), 857-871. doi: 10.1007/s40995-016-0113-9 [22] A. K. Mittal, A space-time pseudospectral method for solving multi-dimensional quasi-linear parabolic partial differential (Burgers') equations, Appl. Numer. Math., 2024, 195, 39-53. doi: 10.1016/j.apnum.2023.09.005 [23] R. C. Mittal and R. K. Jain, Numerical solutions of nonlinear Burgers' equation with modified cubic b-splines collocation method, Appl. Math. Comput., 2012, 218, 7839-7855. [24] R. C. Mittal and R. Jiwari, Differential quadrature method for two-dimensional Burgers' equations, Int. J. Comput. Methods Eng. Sci. Mech., 2009, 10(6), 450-459. doi: 10.1080/15502280903111424 [25] R. C. Mittal and R. Rohila, A study of one dimensional nonlinear diffusion equations by Bernstein polynomial based differential quadrature method, J. Math. Chem., 2017, 55(2), 673-695. doi: 10.1007/s10910-016-0703-y [26] R. C. Mittal and A. Tripathi, Numerical solutions of two-dimensional Burgers' equations using modified B-cubic B-spline finite elements, Eng. Comput., 2015, 32, 1275-1306. doi: 10.1108/EC-04-2014-0067 [27] V. Mukundan and A. Awasthi, Linearized implicit numerical method for Burgers' equation, Nonlinear Eng., 2016, 5, 219-234. [28] M. Palav and V. Pradhan, Efficient numerical solution of Burgers' equation using collocation method based on re-defined uniform hyperbolic polynomial B-splines, J. Appl. Math. Comput., 2025, 1865-2085. [29] K. Pandey, L. Verma and A. K. Verma, On a finite difference scheme for Burgers' equation, Appl. Math. Comput., 2009, 215(6), 2206-2214. [30] K. Shah, Solution of Burgers' equation in a one-dimensional groundwater recharge by spreading using q-Homotopy analysis method, Eur. J. Pure Appl. Math., 2016, 9, 114-124. [31] M. A. Shallal, A. H. Taqi, B. F. Jumaa, H. Rezazadeh and M. Inc, Numerical solutions to the 1-D Burgers' equation by a cubic Hermite finite element method, Indian J. Phys., 2022, 96, 3831-3836. doi: 10.1007/s12648-022-02304-4 [32] H. Shukla, M. Tamsir, V. Srivastava and J. Kumar, Numerical solution of two dimensional coupled viscous Burger equation using modified cubic B-spline differential quadrature method, AIP Adv., 2014, 117134, 1-10. [33] V. P. Shyaman, A. Sreelakshmi and A. Awasthi, A higher order implicit adaptive finite point method for the Burgers' equation, J. Diff. Eq. Appl., 2023, 29(3), 235-269. [34] V. Srivastava, S. Singh and M. Awasthi, Numerical solutions of coupled Burgers' equations by an implicit finite-difference scheme, AIP Adv., 2013, 082131, 1-7. [35] C. C. Tsai, Y. T. Shih, Y. T. Lin and H. C. Wang, Tailored finite point method for solving one-dimensional Burgers' equation, Int. J. Comput. Math., 2017, 94(4), 800-812. [36] Y. Uçar, N. M. Yaǧmurlu and M. K. Yiǧit, Numerical solution of the coupled Burgers equation by trigonometric B-spline collocation method, Math. Meth. Appl. Sci., 2023, 46(5), 6025-6041. [37] S. D. Wang, T. F. Ma, L. L. Wu and X. J. Yang, Two high-order compact finite difference schemes for solving the nonlinear generalized Benjamin-Bona-Mahony-Burgers equation, Appl. Math. Comput., 2025, 496, 129360. [38] L. Yang and X. Pu, Derivation of the Burgers' equation from the gas dynamics, Commun. Math. Sci., 2016, 14, 671-682. [39] X. J. Yang, Y. B. Ge and B. Lan, A class of compact finite difference schemes for solving the 2D and 3D Burgers' equations, Math. Comput. Simulat., 2021, 185, 510-534. [40] X. J. Yang, Y. B. Ge and L. Zhang, A class of high-order compact difference schemes for solving the Burgers' equations, Appl. Math. Comput., 2019, 358, 394-417. [41] T. Zhanlav, O. Chuluunbaatar and V. Ulziibayar, Higher-order accurate numerical solution of unsteady Burgers' equation, Appl. Math. Comput., 2015, 250, 701-707. [42] H. Zhu, H. Shu and M. Ding, Numerical solutions of two-dimensional Burgers' equations by discrete adomian decomposition method, Comput. Math. Appl., 2010, 60(3), 840-848. -
-
Figures(8) / Tables(16)
Export File
Citation
Xueqing Miao, Jiaye Gan, Tingfu Ma, Lili Wu. A LINEAR TIME-SPACE HIGH-ORDER COMPACT FINITE DIFFERENCE SCHEME FOR SOLVING THE ONE-DIMENSIONAL NONLINEAR BURGERS' EQUATION[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3226-3245. doi: 10.11948/20240527
Format
Content
DownLoad:
-
Figure 1.
The exact solution (red) and the numerical solution (black) of Example 4.1 obtained using the LHOC scheme for various values of kinematic viscosity (a)
$ \varepsilon= 0.01 $ $ \varepsilon= 0.001 $ $ \varepsilon= 0.0001 $ $ h=0.01 $ $ \tau=0.001 $ $ T=3 $ -
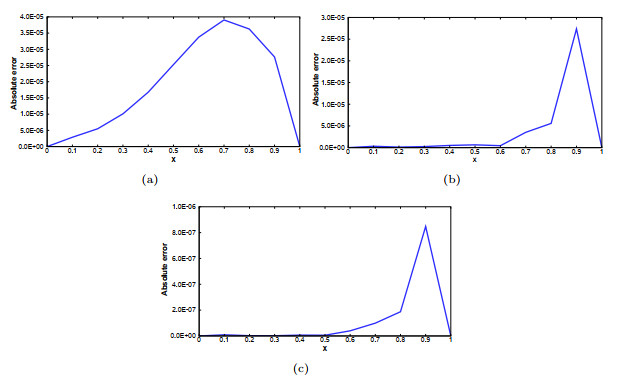
Figure 2.
Absolute errors of Example 4.1 at
$ T = 1 $ $ h = 0.1 $ $ \tau=0.01 $ $ \varepsilon= 0.1 $ $ \varepsilon= 0.01 $ $ \varepsilon= 0.001 $ -
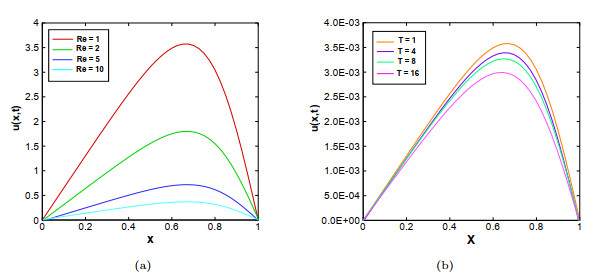
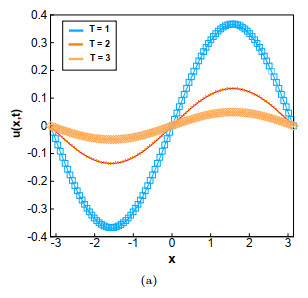
Figure 3.
(a) the numerical solution of the LHOC scheme when
$ Re = 1/\varepsilon = 1, \; 2, \; 5, \; 10, $ $ N = 40, $ $ T = 0.001, $ $ \tau= 0.0001, $ $ T = 1, \; 4, \; 8, \; 16, $ $ N = 40, $ $ \varepsilon = 0.001, $ $ \tau= 0.01 $ -
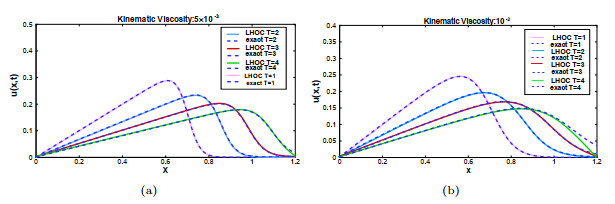
Figure 4.
The exact solution and the numerical solution of Example 4.2 obtained using the LHOC scheme with
$ h = 0.005 $ $ \tau = 0.001 $ $ T =1, \; 2, \; 3, \; 4 $ $ \varepsilon=0.005 $ $ \varepsilon= 0.01 $ -
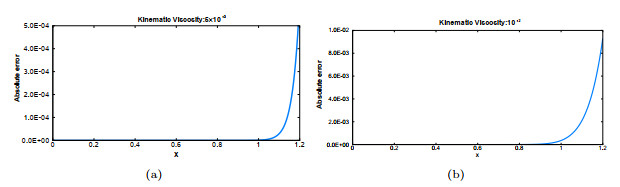
Figure 5.
Absolute errors of Example 4.2 with
$ h = 0.005 $ $ \tau = 0.001 $ $ T = 3 $ $ \varepsilon=0.005 $ $ \varepsilon= 0.01. $ -
Figure 6.
Numerical solution of LHOC scheme of Example 4.3 for values of
$ N = 100 $ $ \tau = 0.001 $ $ k_1 = -2 $ $ k_2 = k_3 = 1 $ $ T = 1, \; 2, $ -
Figure 7.
Exact and numerical solutions of Example 4.4 for values of
$ a_{0} = 0.05 $ $ k_{1} =-1 $ $ k_{2} =0.1 $ $ k_3 = 0.2 $ $ \tau=0.001 $ $ N=51 $ -
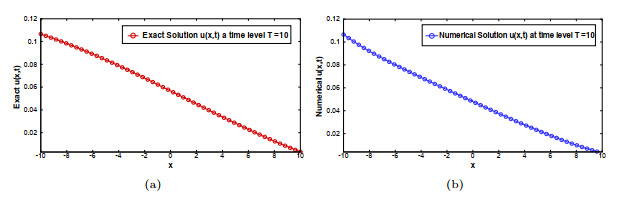
Figure 8.
Exact and numerical solutions of Example 4.4 for values of
$ a_{0} = 0.05 $ $ k_{1} =-1 $ $ k_{2} =0.1 $ $ k_3 = 0.2 $ $ \tau=0.001 $ $ N=51 $