| Citation: | Jing Li, Gongsheng Tong, Rouzi Duan, Shanlin Qin. TIKHONOV REGULARIZATION METHOD OF AN INVERSE SPACE-DEPENDENT SOURCE PROBLEM FOR A TIME-SPACE FRACTIONAL DIFFUSION EQUATION[J]. Journal of Applied Analysis & Computation, 2021, 11(5): 2387-2401. doi: 10.11948/20200397 |
TIKHONOV REGULARIZATION METHOD OF AN INVERSE SPACE-DEPENDENT SOURCE PROBLEM FOR A TIME-SPACE FRACTIONAL DIFFUSION EQUATION
-
Abstract
The aim of this paper is to identify a space-dependent source term in the time-space fractional diffusion equation with an initial-boundary data and an additional measurement data at the final time point. A series expression for the solution of the direct problem is used to transfer the inverse problem into the first type of Fredholm integral equation. Before solving the inverse problem, the uniqueness of its solution is proved. We then use the Tikhonov regularization method to deal with the integral equation and obtain a series expression for the regularized solution of the inverse problem. Moreover, according to the prior and the posterior regularization parameter selection rules, we prove the convergence rates of the regularization solution. Finally, we provide some numerical experiments to show the effectiveness of our method.
-

-
References
[1] N. M. Dien, D. N. D. Hai, T. Q. Viet and D. D. Trong, On Tikhonov¡¯s method and optimal error bound for inverse source problem for a time-fractional diffusion equation, Comput. Math. Appl., 2020, 80(1), 61-81. doi: 10.1016/j.camwa.2020.02.024 [2] H. W. Engl, M. Hanke and A. Neubauer, Regularization of inverse problem, Kluwer Academic Publishers, Netherlands, 1996. [3] Fa and K. Sau, Fractal and generalized Fokker Planck equations: description of the characterization of anomalous diffusion in magnetic resonance imaging, J. Stat. Mech. Theory Exp., 2017, 2017(3), 033207. doi: 10.1088/1742-5468/aa61c6 [4] S. Fedotov and N. Korabel, Subdiffusion in an external potential: anomalous effects hiding behind normal behavior, Phys. Rev. E., 2015, 91(4), 042112. [5] B. Guo, X. Pu and F. Huang, Fractional partial differential equations and their numerical solutions, Science Press, Beijing, 2015. [6] P. C. Hansen, Analysis of discrete ill-posed problems by means of the L-curve, SIAM Review., 1992, 34(4), 561-580. doi: 10.1137/1034115 [7] K. M. Hanke and L. P. C. Hansen, Regularization methods for large-scale problems, Surveys Math. Indust., 1993, 3, 253-315. [8] P. C. Hansen, Regularization tools: a Matlab package for analysis and solution of discrete ill-posed problems, Numer. Algorithms., 1994, 6(1), 1-35. doi: 10.1007/BF02149761 [9] P. K. Kang, M. Dentz, T. L. Borgne and S. L, Anomalous transport in disordered fracture networks: spatial Markov model for dispersion with variable injection models, Adv. Water Resour., 2017, 106, 80-94. [10] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and applications of fractional differential equations, North-Holland Math. Stud., 2006, 204, vii-x. doi: 10.1016/S0304-0208(06)80001-0 [11] A. Kirsch, An introduction to the mathematical theory of inverse problem, Springer, New York, 2011. [12] C. Li and M. Cai, Theory and numerical approximations of fractional integrals and derivatives, Society for Industrial and Applied Mathematics, Philadelphia, 2019. [13] J. Li and B. Guo, Parameter identification in fractional differential equations, Acta Math. Sci., 2013, 33, 855-864. doi: 10.1016/S0252-9602(13)60045-4 [14] J. Li, F. Liu, L. Feng and I. Turner, A novel finite volume method for the Riesz space distributed order advection-diffusion equation, Appl. Math. Model., 2017, 46, 536-553. doi: 10.1016/j.apm.2017.01.065 [15] Y. Li and T. Wei, An inverse time-dependent source problem for a time-space fractional diffusion equation, Appl. Comput. Math., 2018, 336, 257-271. [16] F. Liu, L. Feng, V. Anh and J. Li, Unstructured-mesh Galerkin finite element method for the two-dimensional multi-term time-space fractional Bloch-Torrey equations on irregular convex domains, Comput. Math. Appl., 2019, 78(5), 1637-1650. doi: 10.1016/j.camwa.2019.01.007 [17] J. Liu, M. Yamamoto and L. Yan, On the reconstruction of unknown time-dependent boundary sources for time fractional diffusion process by distributing measurement, Inverse Probl., 2016, 32, 015009. doi: 10.1088/0266-5611/32/1/015009 [18] H. Pollard, The completely monotonic character of the Mittag-Leffler function $E_\alpha(-X)$, Bull. Amer. Math. Soc., 1948, 54(1948), 1115-1116. [19] K. Sakamoto and M. Yamamoto, Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems, J. Math. Anal. Appl., 2011, 382(1), 426-447. doi: 10.1016/j.jmaa.2011.04.058 [20] I. M. Sokolov and J. Klafter, From diffusion to anomalous diffusion: a century after Einstein¡¯s Brownian motion, Chaos, 2005, 15, 26103. doi: 10.1063/1.1860472 [21] C. Sun and J. Liu, An inverse source problem for distributed order time-fractional diffusion equation, Inverse Probl., 2020, 36(5), 055008. doi: 10.1088/1361-6420/ab762c [22] Z. Sun and G. Gao, Finite difference methods for fractional differential equations, Science Press, Beijing, 2016. [23] S. Tatar, R. Tnaztepe and S. Ulusoy, Determination of an unknown source term in a space-time fractional diffusion equation, J. Fract. Calc. Appl., 2015, 6(1), 83-90. [24] S. Tatar, R. Tnaztepe and S. Ulusoy, Simultaneous inversion for the exponents of the fractional time and space derivatives in the space-time fractional diffusion equation, Appl. Anal., 2016, 95(1), 1-23. doi: 10.1080/00036811.2014.984291 [25] S. Tatar and S. Ulusoy, An inverse source problem for a one-dimensional space-time fractional diffusion equation, Appl. Anal., 2014, 94(11), 1-12. [26] N. Tuan and L. Long, Fourier truncation method for an inverse source problem for space-time fractional diffusion equation, Electron J. Differ. Eq., 2017, 2017(122), 1-16. [27] H. Wang and T. S. Basu, A fast finite difference method for two-dimensional space-fractional diffusion equations, SIAM J. Comput., 2012, 3(4), 1032-1044. [28] T. Wei and J. Wang, A modified quasi-boundary value method for an inverse source problem of the time-fractional diffusion equation, Appl. Numer. Math., 2014, 78, 95-111. doi: 10.1016/j.apnum.2013.12.002 [29] T. Wei, X. Li and Y. Li, An inverse time-dependent source problem for a time-fractional diffusion equation, Inverse Probl., 2016, 32, 085003. doi: 10.1088/0266-5611/32/8/085003 [30] T. Wei and Y. Zhang, The backward problem for a time-fractional diffusion-wave equation in a bounded domain, Comput. Math. Appl., 2018, 75(10), 3632-3648. doi: 10.1016/j.camwa.2018.02.022 [31] Y. Zhu and Z. Sun, A high order difference scheme for the space and time fractional Bloch-Torrey equation, Comput. Methods Appl. Math., 2018, 18(1), 147-164. doi: 10.1515/cmam-2017-0034 -
-
-
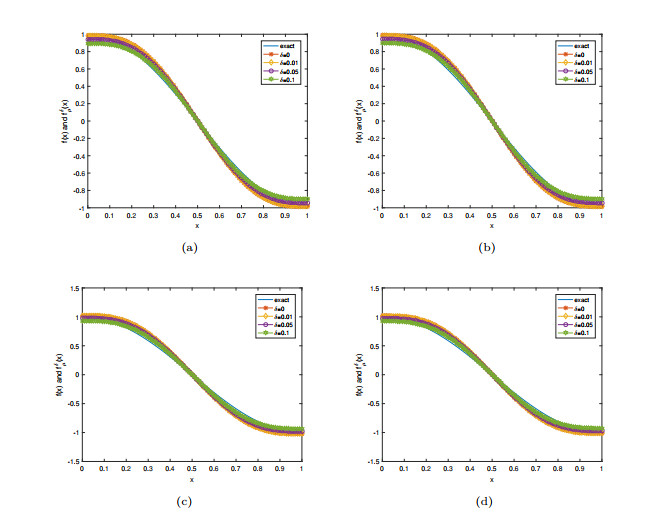
Figure 1. The numerical results of the inverse source term
$ f(x) $ for (a)$ \alpha = 0.3, \beta = 1.2 $ ; (b)$ \alpha = 0.3, \beta = 1.8 $ ; (c)$ \alpha = 0.7, \beta = 1.2 $ ; and (d)$ \alpha = 0.7, \beta = 1.8 $ with different noise levels$ \delta = 0, 0.01, 0.05\;~ and\;~ 0.1 $




 DownLoad:
DownLoad: