| Citation: | Makram Hamouda, Mohamed Ali Hamza. A BLOW-UP RESULT FOR THE WAVE EQUATION: THE SCALE-INVARIANT DAMPING AND MASS TERM WITH COMBINED NONLINEARITIES[J]. Journal of Applied Analysis & Computation, 2022, 12(5): 1816-1841. doi: 10.11948/20210361 |
A BLOW-UP RESULT FOR THE WAVE EQUATION: THE SCALE-INVARIANT DAMPING AND MASS TERM WITH COMBINED NONLINEARITIES
-
Abstract
We are interested in this article in studying the damped wave equation in the scale-invariant case with mass term and two combined nonlinearities. More precisely, we consider the following equation:
$ { } (E) \quad u_{tt}-\Delta u+\frac{\mu}{1+t}u_t+\frac{\nu^2}{(1+t)^2}u=|u_t|^p+|u|^q, \quad \mbox{in}\ {{\mathbb{R}}}^N\times[0,\infty), $
with small initial data. Under some assumptions on the mass and damping coefficients, $ \nu $ and $ \mu>0 $, respectively, we show that blow-up region and the lifespan bound of the solution of $ (E) $ remain the same as the ones obtained in [
12 ] in the case of a mass-free wave equation, i.e. $ (E) $ with $ \nu=0 $. Furthermore, using in part the computations done for $ (E) $, we enhance the result in [30 ] on the Glassey conjecture for the solution of $ (E) $ with omitting the nonlinear term $ |u|^q $. Indeed, the blow-up region is extended to $ p \in (1, p_G(N+\mu)] $ yielding, hence, a better estimate of the lifespan when $ (\mu-1)^2-4\nu^2<1 $. Otherwise, the two results coincide. Finally, we may conclude that the mass term has no influence on the dynamics of $ (E) $ (resp. $ (E) $ without the nonlinear term $ |u|^q $). -

-
References
[1] W. Chen, S. Lucente and A. Palmieri, Nonexistence of global solutions for generalized Tricomi equations with combined nonlinearity, Nonlinear Analysis: Real World Applications, 2021, 61, 103354. doi: 10.1016/j.nonrwa.2021.103354 [2] M. D'Abbicco, The threshold of effective damping for semilinear wave equations, Math. Methods Appl. Sci., 2015, 38(6), 1032-1045. doi: 10.1002/mma.3126 [3] M. D'Abbicco and S. Lucente, A modified test function method for damped wave equations, Adv. Nonlinear Stud., 2013, 13(4), 867-892. doi: 10.1515/ans-2013-0407 [4] M. D'Abbicco and S. Lucente, NLWE with a special scale invariant damping in odd space dimension, Conference Publications, 2015, 2015 (special), 312-319. [5] M. D'Abbicco, S. Lucente and M. Reissig, A shift in the Strauss exponent for semilinear wave equations with a not effective damping, J. Differential Equations, 2015, 259(10), 5040-5073. doi: 10.1016/j.jde.2015.06.018 [6] W. Dai, D. Fang and C. Wang, Global existence and lifespan for semilinear wave equations with mixed nonlinear terms, J. Differential Equations, 2019, 267(5), 3328-3354. doi: 10.1016/j.jde.2019.04.007 [7] A. Erdelyi, W. Magnus, F. Oberhettinger and F. G. Tricomi, Higher Transcendental Functions, vol. 2, McGraw-Hill, New-York, 1953. [8] R. E. Gaunt, Inequalities for modified Bessel functions and their integrals, J. Mathematical Analysis and Applications, 2014, 420, 373-386. doi: 10.1016/j.jmaa.2014.05.083 [9] M. F. Ben Hassen, M. Hamouda, M. A. Hamza and H. K. Teka, Nonexistence result for the generalized Tricomi equation with the scale-invariant damping, mass term and time derivative nonlinearity, To appear in Asymptotic Analysis, 2021, 1-21. [10] M. Hamouda and M. A. Hamza, Blow-up and lifespan estimate for the generalized Tricomi equation with mixed nonlinearities, Advances in Pure and Applied Mathematics, 2021, 12, special issue, 54-70. DOI: 10.21494/ISTE.OP.2021.0698. [11] M. Hamouda and M. A. Hamza, Blow-up for wave equation with the scale-invariant damping and combined nonlinearities, Math. Methods Appl. Sci., 2020, 1-10. https://doi.org/10.1002/mma.6817. doi: 10.1002/mma.6817 [12] M. Hamouda and M. A. Hamza, Improvement on the blow-up of the wave equation with the scale-invariant damping and combined nonlinearities, Nonlinear Anal. Real World Appl., 2021, 59, 103275. https://doi.org/10.1016/j.nonrwa.2020.103275. doi: 10.1016/j.nonrwa.2020.103275 [13] W. Han and Y. Zhou, Blow up for some semilinear wave equations in multi-space dimensions, Comm. Partial Differential Equations, 2014, 39(4), 65-665. [14] K. Hidano and K. Tsutaya, Global existence and asymptotic behavior of solutions for nonlinear wave equations, Indiana Univ. Math. J., 1995, 44, 1273-1305. [15] K. Hidano, C. Wang and K. Yokoyama, Combined effects of two nonlinearities in lifespan of small solutions to semi-linear wave equations, Math. Ann., 2016, 366(1-2), 667-694. doi: 10.1007/s00208-015-1346-1 [16] K. Hidano, C. Wang and K. Yokoyama, The Glassey conjecture with radially symmetric data, J. Math. Pures Appl., 2012, 98(5), 518-541. doi: 10.1016/j.matpur.2012.01.007 [17] F. John, Blow-up for quasilinear wave equations in three space dimensions, Comm. Pure Appl. Math., 1981, 34, 29-51. doi: 10.1002/cpa.3160340103 [18] F. John, Blow-up of solutions of nonlinear wave equations in three space dimensions, Manuscripta Math., 1979, 28(1-3), 235-268. doi: 10.1007/BF01647974 [19] N. Lai, N. M. Schiavone and H. Takamura, Heat-like and wave-like lifespan estimates for solutions of semilinear damped wave equations via a Kato's type lemma, Journal of Differential Equations, 2020, 269(12), 11575-11620. doi: 10.1016/j.jde.2020.08.020 [20] N. Lai and H. Takamura, Nonexistence of global solutions of nonlinear wave equations with weak time-dependent damping related to Glassey's conjecture, Differential Integral Equations, 2019, 32(1-2), 37-48. [21] W. N. Nascimento, Klein-Gordon Models with Non-Effective Time-Dependent Potential, (Ph. D. thesis) Univ. Federal de São Carlos, 2016. [22] W. Nunes do Nascimento, A. Palmieri and M. Reissig, Semi-linear wave models with power non-linearity and scale-invariant time-dependent mass and dissipation, Mathematische Nachrichten, 2017, 290(11-12), 1779-1805. doi: 10.1002/mana.201600069 [23] A. Palmieri, A global existence result for a semilinear wave equation with scale-invariant damping and mass in even space dimension, Math. Meth. Appl. Sci., 2019, 1-27. https://doi.org/10.1002/mma.5542. doi: 10.1002/mma.5542 [24] A. Palmieri, A note on a conjecture for the critical curve of a weakly coupled system of semilinear wave equations with scale-invariant lower order terms, Mathematical Methods in the Applied Sciences, 2020, 43(11), 6702-6731. doi: 10.1002/mma.6412 [25] A. Palmieri, Global in time existence and blow‐up results for a semilinear wave equation with scale‐invariant damping and mass, PhD thesis, TU Bergakademie Freiberg, 2018. [26] A. Palmieri, Global existence of solutions for semi-linear wave equation with scale-invariant damping and mass in exponentially weighted spaces, Journal of Mathematical Analysis and Applications, 2018, 461(2), 1215-1240. doi: 10.1016/j.jmaa.2018.01.063 [27] A. Palmieri, Global existence results for a semilinear wave equation with scale-invariant damping and mass in odd space dimension, In New Tools for Nonlinear PDEs and Application, Birkhäuser, Cham, 2019, 305-369. [28] A. Palmieri and M. Reissig, A competition between Fujita and Strauss type exponents for blow-up of semi-linear wave equations with scale-invariant damping and mass, J. Differential Equations, 2019, 266(2-3), 1176-1220. doi: 10.1016/j.jde.2018.07.061 [29] A. Palmieri and M. Reissig, Semi-linear wave models with power non-linearity and scale-invariant time-dependent mass and dissipation, Ⅱ, Mathematische Nachrichten, 2018, 291(11-12), 1859-1892. doi: 10.1002/mana.201700144 [30] A. Palmieri and Z. Tu, A blow-up result for a semilinear wave equation with scale-invariant damping and mass and nonlinearity of derivative type, Calc. Var., 2021, 60, 72. https://doi.org/10.1007/s00526-021-01948-0. doi: 10.1007/s00526-021-01948-0 [31] A. Palmieri and Z. Tu, Lifespan of semilinear wave equation with scale invariant dissipation and mass and sub-Strauss power nonlinearity, J. Math. Anal. Appl., 2019, 470(1), 447-469. doi: 10.1016/j.jmaa.2018.10.015 [32] M. A. Rammaha, Finite-time blow-up for nonlinear wave equations in high dimensions, Comm. Partial Differential Equations, 1987, 12(6), 677-700. doi: 10.1080/03605308708820506 [33] T. C. Sideris, Global behavior of solutions to nonlinear wave equations in three space dimensions, Comm. Partial Differential Equations, 1983, 8(12), 1291-1323. doi: 10.1080/03605308308820304 [34] W. A. Strauss, Nonlinear scattering theory at low energy, J. Functional Analysis, 1981, 41(1), 110-133. doi: 10.1016/0022-1236(81)90063-X [35] Z. Tu, and J. Lin, A note on the blowup of scale invariant damping wave equation with sub-Strauss exponent, preprint, arXiv: 1709.00866v2, 2017. [36] Z. Tu, and J. Lin, Life-span of semilinear wave equations with scale-invariant damping: critical Strauss exponent case, Differential Integral Equations, 2019, 32(5-6), 249-264. [37] N. Tzvetkov, Existence of global solutions to nonlinear massless Dirac system and wave equation with small data, Tsukuba J. Math., 1998, 22, 193-211. [38] K. Wakasugi, Critical exponent for the semilinear wave equation with scale invariant damping, In: M. Ruzhansky, V. Turunen (Eds. ) Fourier Analysis, Trends in Mathematics, Birkhäuser, Cham, 2014. https://doi.org/10.1007/978-3-319-02550-619. [39] C. Wang and H. Zhou, Almost global existence for semilinear wave equations with mixed nonlinearities in four space dimensions, J. Math. Anal. Appl., 2018, 459(1), 236-246. doi: 10.1016/j.jmaa.2017.10.058 [40] B. Yordanov and Q. Zhang, Finite time blow up for critical wave equations in high dimensions, J. Funct. Anal., 2006, 231, 361-374. doi: 10.1016/j.jfa.2005.03.012 [41] Y. Zhou, Blow up of solutions to semilinear wave equations with critical exponent in high dimensions, Chin. Ann. Math. Ser. B, 2007, 28(2), 205-212. doi: 10.1007/s11401-005-0205-x [42] Y. Zhou, Blow-up of solutions to the Cauchy problem for nonlinear wave equations, Chin. Ann. Math., 2001, 22B(3), 275-280. -
-
-
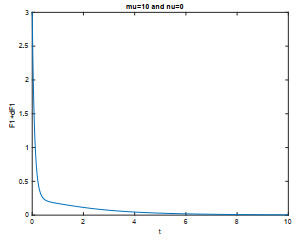
Figure 1. The case
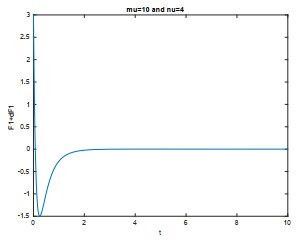
$ \mu=10, \nu=0 $ (the free-mass case with$ \delta >0 $ ). - Figure 2. The case µ = 10, ν = 4 which corresponds to δ > 0.
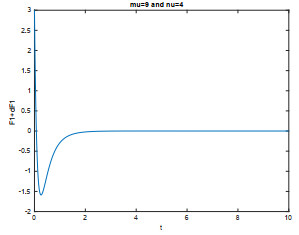
- Figure 3. The case µ = 9, ν = 4 which corresponds to δ = 0.
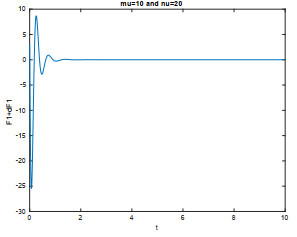
- Figure 4. The case µ = 10, ν = 20 which corresponds to δ < 0.




 DownLoad:
DownLoad: