| Citation: | Wenli Wang, Caiqin Song. A NOVEL ITERATIVE METHOD FOR SOLVING THE COUPLED SYLVESTER-CONJUGATE MATRIX EQUATIONS AND ITS APPLICATION IN ANTILINEAR SYSTEM[J]. Journal of Applied Analysis & Computation, 2023, 13(1): 249-274. doi: 10.11948/20220032 |
A NOVEL ITERATIVE METHOD FOR SOLVING THE COUPLED SYLVESTER-CONJUGATE MATRIX EQUATIONS AND ITS APPLICATION IN ANTILINEAR SYSTEM
-
Abstract
This paper is devoted to constructing a modified relaxed gradient based iterative (MRGI) algorithm to solve the coupled Sylvester-conjugate matrix equations (CSCMEs) based on the hierarchical identification principle. Convergence analysis shows that the proposed algorithm is effective for arbitrary initial matrices. Further, we apply the MRGI algorithm to study a more general coupled Sylvester conjugate matrix equations and give a sufficient condition to guarantee that the iterative solution converges to the exact solution. Two numerical experiments are provided to demonstrate that the MRGI algorithm has better efficiency and accuracy than the three existing algorithms, which are presented by Wu et al. (2010) and Huang and Ma (2018). Finally, we derive an application of MRGI algorithm in discrete-time antilinear system.
-

-
References
[1] K. Adisorn and C. Pattrawut, Approximated least-squares solutions of a generalized Sylvester-transpose matrix equation via gradient-descent iterative algorithm, Advances in Difference Equations, 2021, 2021, 266. doi: 10.1186/s13662-021-03427-4 [2] K. Adison, C. Pattrawut and L. Wicharn, Convergence analysis of gradient-based iterative algorithms for a class of rectangular Sylvester matrix equations based on Banach contraction principle, Advances in Difference Equations, 2021, 2021, 17. doi: 10.1186/s13662-020-03185-9 [3] R. Agarwal, S. Hristova, D. O'Regan and K. Stefanova, Iterative Algorithm for Solving Scalar Fractional Differential Equations with Riemann-Liouville Derivative and Supremum, Algorithms, 2020, 13(8), 184. doi: 10.3390/a13080184 [4] M. Dehghan and M. Hajarian, The generalised Sylvester matrix equations over the generalised bisymmetric and skew-symmetric matrices, International Journal of Systems Science, 2012, 43(8), 1580–1590. doi: 10.1080/00207721.2010.549584 [5] M. Dehghan and R. Mohammadi-Arani, Generalized product-type methods based on bi-conjugate gradient (GPBiCG) for solving shifted linear systems, Comput. Appl. Math., 2016, 36(4), 1–16. [6] F. Ding, X. Liu and J. Ding, Iterative solutions of the generalized Sylvester matrix equations by using the hierarchical identification principle, Appl. Math. Comput., 2008, 197(1), 41–50. [7] F. Ding, F. Wang, L. Xu and M. Wu, Decomposition based least squares iterative identification algorithm for multivariate pseudo-linear ARMA systems using the data filtering, J. Frankl. Inst., 2017, 354(3), 1321–1339. doi: 10.1016/j.jfranklin.2016.11.030 [8] M. Hajarian, Solving the general Sylvester discrete-time periodic matrix equations via the gradient based iterative method, Appl. Math. Lett., 2016, 52, 87–95. doi: 10.1016/j.aml.2015.08.017 [9] M. Hajarian, Gradient based iterative algorithm to solve general coupled discretetime periodic matrix equations over generalized reflexive matrices, Math. Model. Anal., 2016, 21, 533–549. doi: 10.3846/13926292.2016.1186119 [10] M. Hajarian, New finite algorithm for solving the generalized nonhomogeneous Yakubovich-transpose matrix equation, Asian J. Control, 2017, 19, 164–172. doi: 10.1002/asjc.1343 [11] M. Hajarian, Convergence of HS version of BCR algorithm to solve the generalized Sylvester matrix equation over generalized reflexive matrices, J. Frankl. Inst., 2017, 354, 2340–2357. doi: 10.1016/j.jfranklin.2017.01.008 [12] M. Hajarian, Reflexive periodic solutions of general periodic matrix equations, Mathematical Methods in the Applied Sciences, 2019, 42(10), 3527–3548. doi: 10.1002/mma.5596 [13] M. Hajarian, Three types of biconjugate residual method for general periodic matrix equations over generalized bisymmetric periodic matrices, Transactions of the Institute of Measurement and Control, 2019, 41(10), 2708–2725. doi: 10.1177/0142331218808859 [14] B. Huang and C. Ma, Gradient-based iterative algorithms for generalized coupled Sylvester-conjugate matrix equations, Comput. Math. Appl., 2018, 75, 2295–2310. doi: 10.1016/j.camwa.2017.12.011 [15] B. Huang and C. Ma, The relaxed gradient-based iterative algorithms for a class of generalized coupled Sylvester-conjugate matrix equations, J. Frankl. Inst., 2018, 355, 3168–3195. doi: 10.1016/j.jfranklin.2018.02.014 [16] Y. Ji, H. J. Chizeck, X. Feng and K. A. Loparo, Stability and control of discrete-time jump linear systems, Control Theory Adv. Technol., 1991, 7(2), 247–270. [17] T. Jiang and M. Wei, On solutions of the matrix equations $X-AXB=C$ and $X-A\overline{X}B=C$, Linear Algebra and its Applications, 2003, 367, 225–233. doi: 10.1016/S0024-3795(02)00633-X [18] Q. Niu, X. Wang and L. Lu, A relaxed gradient based algorithm for solving Sylvester equations, Asian J. Control, 2011, 13, 461–464. doi: 10.1002/asjc.328 [19] X. Sheng, A relaxed gradient based algorithm for solving generalized coupled Sylvester matrix equations, J. Frankl. Inst., 2018, 355, 4282–4297. doi: 10.1016/j.jfranklin.2018.04.008 [20] C. Song, G. Chen and L. Zhao, Iterative solutions to coupled Sylvester-transpose matrix equations, Appl. Math. Model., 2011, 35(10), 4675–4683. doi: 10.1016/j.apm.2011.03.038 [21] C. Vanhille, A note on the convergence of the irrational Halley¡¯s iterative algorithm for solving nonlinear equations, International Journal of Computer Mathematics, 2020, 97(9), 1840–1848. doi: 10.1080/00207160.2019.1664736 [22] X. Wang, L. Dai and D. Liao, A modified gradient based algorithm for solving Sylvester equations, Appl. Math. Comput., 2012, 218, 5620–5628. [23] X. Wang and D. Liao, The optimal convergence factor of the gradient based iterative algorithm for linear matrix equations, Filomat, 2012, 26, 607–613. doi: 10.2298/FIL1203607W [24] A. Wu, G. Feng, G. Duan and W. Wu, Iterative solutions to coupled Sylvester-conjugate matrix equations, Comput. Math. Appl., 2010, 60(1), 54–66. doi: 10.1016/j.camwa.2010.04.029 [25] A. Wu, L. Lv and G. Duan, Iterative algorithms for solving a class of complex conjugate and transpose matrix equations, Appl. Math. Comput., 2011, 217(21), 8343–8353. [26] A. Wu, X. Zeng, G. Duan and W. Wu, Iterative solutions to the extended Sylvester-conjugate matrix equatinos, Appl. Math. Comput., 2010, 217(1), 130–142. [27] Y. Xie and C. Ma, The accelerated gradient based iterative algorithm for solving a class of generalized Sylvester-transpose matrix equation, Appl. Math. Comput., 2016, 273, 1257–1269. [28] T. Yan and C. Ma, The BCR algorithms for solving the reflexive or anti-reflexive solutions of generalized coupled Sylvester matrix equations, Journal of the Franklin Institute, 2020, 357, 12787–12807. doi: 10.1016/j.jfranklin.2020.09.030 [29] L. Zhang, B. Huang and J. Lam, H∞ model reduction of Markovian jump linear systems, Syst. Control Lett., 2003, 50, 103–118. doi: 10.1016/S0167-6911(03)00133-6 [30] H. Zhang, Reduced-rank gradient-based algorithms for generalized coupled Sylvester matrix equations and its applications, Comput. Math. Appl., 2015, 70, 2049–2062. doi: 10.1016/j.camwa.2015.08.013 [31] H. Zhang and F. Ding, A property of the eigenvalues of the symmetric positive definite matrix and the iterative algorithm for coupled Sylvester matrix equations, J. Frankl. Inst., 2014, 351, 340–357. doi: 10.1016/j.jfranklin.2013.08.023 [32] H. Zhang and H. Yin, New proof of the gradient-based iterative algorithm for a complex conjugate and transpose matrix equation, J. Frankl. Inst., 2017, 354, 7585–7603. doi: 10.1016/j.jfranklin.2017.09.005 [33] B. Zhou and G. Duan, Periodic Lyapunov equation based approaches to the stabilization of continuous-time periodic linear systems, IEEE Trans. Autom. Control, 2012, 57, 2139–2146. doi: 10.1109/TAC.2011.2181796 [34] B. Zhou, J. Lam and G. Duan, Gradient-based maximal convergence rate iterative method for solving linear matrix equations, International Journal of Computer Mathematics, 2010, 87(3), 515–527. doi: 10.1080/00207160802123458 -
-
-
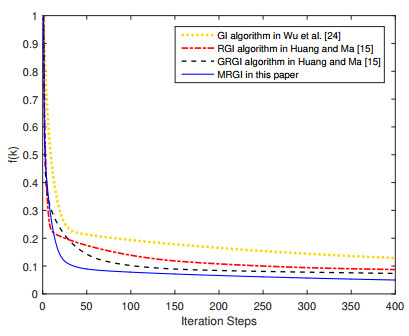
Figure 1.
Comparison of convergence curve
-
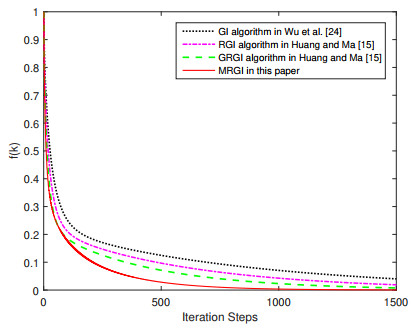
Figure 2.
Comparison of convergence curves
-
Figure 3.
The convergence performance of MRGI for different convergence factors
$ \mu_{1} $ $ \mu_{2} $ $ \omega_{1}=0.4, \omega_{2}=0.6 $




 DownLoad:
DownLoad: