| Citation: | Fanwei Meng, Lin Chen, Xianchao Zhang, Yancong Xu. TRANSMISSION DYNAMICS OF A CHAGAS DISEASE MODEL WITH STANDARD INCIDENCE INFECTION[J]. Journal of Applied Analysis & Computation, 2023, 13(6): 3422-3441. doi: 10.11948/20230071 |
TRANSMISSION DYNAMICS OF A CHAGAS DISEASE MODEL WITH STANDARD INCIDENCE INFECTION
-
Abstract
In this paper, an insect-parasite-host model with Ricker’s type reproduction of triatomines and the standard incidence rate of the interaction between insects and hosts is formulated to study the transmission dynamics of Chagas disease. Two thresholds of the ecological basic reproduction number of triatomines and the epidemiological basic reproduction number of Chagas disease are derived, which determine the dynamics of this model. As a result, the existence of equilibria and the local/global stabilities of the equilibrium are accordingly obtained. Moreover, backward bifurcation, forward bifurcation and saddle-node bifurcation are also shown analytically and numerically. Biologically speaking, Chagas disease may undergo outbreak if the number of bites of per triatomine bug per unit time or the transmission probability from infected bugs to susceptible competent hosts per bite increase.
-

-
References
[1] M. A. Acuña-Zegarra, D. Olmos-Liceaga and J. X. Velasco-Hernš¢ndez, The role of animal grazing in the spread of Chagas disease, J. Theo. Biol., 2018, 457, 19–28. doi: 10.1016/j.jtbi.2018.08.025 [2] C. M. Barbu, E. Dumonteil and S. Gourbiššre, Optimization of control strategies for non-domiciliated triatoma dimidiata, chagas disease vector in the Yucatš¢n Peninsula, Mexico, Plos. Negl. Trop. Dis., 2009, 3(4), e416. doi: 10.1371/journal.pntd.0000416 [3] C. M. Barbu, A. Hong, J. M. Manne, D. S. Small, J. E. Quintanilla Calderš®n, K. Sethuraman, V. Quispe-Machaca, J. Ancca-Juš¢rez, J. G. Cornejo, F. S. del Carpio and M. Chavez, The effects of city streets on an urban disease vector, Plos. Comput. Biol., 2013, 9(1), e1002801. doi: 10.1371/journal.pcbi.1002801 [4] P. Bernard, B. Carolina, S. Eric, R. Isabella, V. Rafael, G. Joaquim, P. M. Jesus, M. Silvia, G. Silvia and P. Ana, The benefit trial: Where do we go from here?, Plos. Negl. Trop. Dis., 2016, 10(2), e0004343. doi: 10.1371/journal.pntd.0004343 [5] L. Chen, X. T. Wu, Y. C. Xu and L. B. Rong, Modelling the dynamics of Trypanosoma rangeli and triatomine bug with logistic growth of vector and systemic transmission, Math. Biosci. Eng., 2022, 19(8). [6] A. B. B. de Oliveira, K. C. C. Alevi, C. H. L. Imperador, F. F. Madeira and M. T. V. de Azeredo Oliveira, Parasite-vector interaction of Chagas disease: A mini-review, Am. J. Trop. Med. Hyg., 2018, 98(3), 653. doi: 10.4269/ajtmh.17-0657 [7] E. J. Doedel, A. R. Champneys, F. Dercole, T. F. Fairgrieve, Yu A. Kuznetsov, B. Oldeman, R. C. Paffenroth, B. Sandstede, X. J. Wang and C. H. Zhang, AUTO-07P: Continuation and Bifurcation Software for Ordinary Differential Equations, US, 2007. [8] P. Dreessche and J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Math. Biosci., 2002, 180, 29–48. doi: 10.1016/S0025-5564(02)00108-6 [9] A. M. Ferreira, L. I. Santos, E. C. Sabino, A. L P. Ribeiro, L. C. Oliveira-da Silva, R. F. Damasceno, M. F. S. V D’Angelo, M. D. C. P Nunes and D. S. A. Haikal, Two-year death prediction models among patients with Chagas Disease using machine learning-based methods, Plos. Negl. Trop. Dis., 2022, 16, e0010356. doi: 10.1371/journal.pntd.0010356 [10] F. Lardeux, Niche invasion, competition and coexistence amongst wild and domestic Bolivian populations of Chagas vector Triatoma infestans (Hemiptera, Reduviidae, Triatominae), C. R. Biol., 2013, 336(4), 183–193. doi: 10.1016/j.crvi.2013.05.003 [11] R. Gurgel-Goncalves, C. Galvao, J. Costa and A. T. Peterson, Geographic distribution of Chagas disease vectors in Brazil based on ecological niche modeling, J. Trop. Med., 2012, 2012(1), 705326. [12] R. E. Gürtler, A. L. Ceballos, P. O-Krasnowski, L. A. Lanati, R. Stariolo and U. Kitron, Strong host-feeding preferences of the vector triatoma infestans modified by vector density: Implications for the epidemiology of Chagas disease, Plos. Negl. Trop. Dis., 2009, 3(5), e447. doi: 10.1371/journal.pntd.0000447 [13] R. E. Gürtler, U. Kitron, M. C. Cecere, E. L. Segura and J. E. Cohen, Sustainable vector control and management of Chagas disease in the Gran Chaco, Argentina, Proc. Natl. Acad. Sci. USA., 2007, 104(41), 16194–16199. doi: 10.1073/pnas.0700863104 [14] D. Huang, Y. Tang and W. Zhang, Distributuion of roots of cubic equations, J. Korea Soc. Math. Educ. ser. b Pure Appl. math, 2010, 12(7), 185–188. [15] K. Imai, T. Murakami, K. Misawa, Y Fujikura, A. Kawana, N. Tarumoto, S. Maesaki and T. Maeda, Optimization and evaluation of the ARCHITECT Chagas assay and in-house ELISA for Chagas disease in clinical settings in Japan, Parasitol. int., 2021, 80, 102221. doi: 10.1016/j.parint.2020.102221 [16] H. Inaba and H. Sekine, A mathematical model for Chagas disease with infection-age-dependent infectivity, Math. Biosci., 2004, 190(1), 39–69. doi: 10.1016/j.mbs.2004.02.004 [17] C. D. O. R. Júnior, P. D. G. Martinez, R. A. A. Ferreira, P. J. Koovits, B. M. Soares, L. L. Ferreira, S. Michelan-Duarte, R. C. Chelucci, A. D. Andricopulo, A. Matheeussen, et al., Hit-to-lead optimization of a 2-aminobenzimidazole series as new candidates for chagas disease, Eur. J. Med. Chem., 2023, 246, 114925. doi: 10.1016/j.ejmech.2022.114925 [18] C. M. Kribs and C. Mitchell, Host switching vs. host sharing in overlapping sylvatic Trypanosoma cruzi transmission cycles, J. Bio. Dynam., 2015, 9(1), 1–31. [19] B. Y. Lee, K. M. Bacon, M. E. Bottazzi and P. J. Hotez, Global economic burden of Chagas disease: A computational simulation model, Lancet Infect. Dis., 2013, 13(4), 342–348. doi: 10.1016/S1473-3099(13)70002-1 [20] B. Y. Lee, K. M. Bacon, A. R. Wateska, M. E. Bottazzi, E. Dumonteil and P. J. Hotez, Modeling the economic value of a Chagas’ disease therapeutic vaccine, Hum. Vaccin. Immunother., 2012, 8(9), 1293–1301. doi: 10.4161/hv.20966 [21] B. Y. Lee, S. M. Bartsch, L. Skrip, D. L. Hertenstein and A. Galvani, Are the London Declaration’s 2020 goals sufficient to control Chagas disease?: Modeling scenarios for the Yucatan Peninsula, Plos. Negl. Trop. Dis., 2018, 12(3), e0006337. doi: 10.1371/journal.pntd.0006337 [22] M. Z. Levy, F. S. M. Chavez, J. G. Cornejo, del Carpio, D. A. Vilhena, F. E. Mckenzie and J. B. Plotkin, Rational spatio-temporal strategies for controlling a Chagas disease vector in urban environments, J. R. Soc. Interface., 2010, 7(48), 1061–1070. doi: 10.1098/rsif.2009.0479 [23] W. H. Organization, Chagas disease in Latin America: An epidemiological update based on 2010 estimates, Wkly. Epidemiol. Rec., 2015, 90(6), 33–43. [24] J. K. Peterson, S. M. Bartsch, B. Y. Lee and A. P. Dobson, Broad patterns in domestic vector-borne Trypanosoma cruzi transmission dynamics: Synanthropic animals and vector control, Parasite. Vector., 2015, 8, 537. doi: 10.1186/s13071-015-1146-1 [25] P. J. Plourde, K. Kadkhoda and M. Ndao, Congenitally transmitted Chagas disease in Canada: a family cluster, Can. Med. Assoc. J., 2017, 189(48), E1489–E1492. doi: 10.1503/cmaj.170648 [26] J. E. Rabinovich, J. A. Leal and de Piñero D. Feliciangeli, Domiciliary biting frequency and blood ingestion of the Chagas’s disease vector Rhodnius prolixus Ståhl (Hemiptera: Reduviidae), in Venezuela, T. Roy. Soc. Trop. Med. H., 1979, 3, 272–283. [27] A. Requena-Mndez, E. Aldasoro, E. De Lazzari, E. Sicuri, M. Brown, D. A. J. Moore, J. Gascon, J. M. and M. M. Rodrigues, Prevalence of Chagas disease in Latin-American migrants living in Europe: A systematic review and meta-analysis, Plos. Negl. Trop. Dis., 2015, 9(2), e0003540. doi: 10.1371/journal.pntd.0003540 [28] P. Rodari, F. Tamarozzi, S. Tais, M. Degani, F. Perandin, D. Buonfrate, E. Nicastri, L. Lepore, M. L. Giancola, S. Carrara and others, Prevalence of Chagas disease and strongyloidiasis among HIV-infected Latin American immigrants in Italy–The CHILI study, Tra. Med. Infect. Di., 2022, 48, 102324. doi: 10.1016/j.tmaid.2022.102324 [29] M. Saavedra, A. Bacigalupo, M. V. Barrera, M. J. Vergara, B. Álvarez-Duhart, C. Muñoz-San Martín, R. Solís and P. E. Cattan, Trypanosoma cruzi infection in the wild Chagas disease vector, Mepraia spinolai: Parasitic load, discrete typing units, and blood meal sources, Acta Tropica, 2022, 229, 106365. doi: 10.1016/j.actatropica.2022.106365 [30] C. J. Schofield, N. G. Williams and T. F. D. C. Marshall, Density-dependent perception of triatomine bug bites, Annals of Tropical Medicine. Parasitology., 1986, 80(3), 351–358. doi: 10.1080/00034983.1986.11812028 [31] H. Smith, Monotone dynamical systems : an introduction to the theory of competitive and cooperative systems, Ams Ebooks Program, 1995, 41(5), 174. [32] L. Stevens, D. M. Rizzo, D. E. Lucero and J. C. Pizarro, Household model of Chagas disease vectors (Hemiptera: Reduviidae) considering domestic, peridomestic, and sylvatic vector populations, J. Med. Entomol., 2013, 50(4), 907–915. doi: 10.1603/ME12096 [33] N. Tomasini, P. G. Ragone, S. Gourbiere, J. P. Aparicio and P. Diosque, Epidemiological modeling of Trypanosoma cruzi: Low stercorarian transmission and failure of host adaptive immunity explain the frequency of mixed infections in humans, Plos. Comput. Biol., 2017, 13. [34] J. X. Velasco-Hernndez, An epidemiological model for the dynamics of Chagas’ disease., Biosystems, 1991, 26(2), 127–134. doi: 10.1016/0303-2647(91)90043-K [35] J. X. Velasco-Hernndez, A model for Chagas disease involving transmission by vectors and blood transfusion, Theor. Popul. Biol., 1994, 46(1), 1–31. doi: 10.1006/tpbi.1994.1017 [36] X. T. Wu, D. Z. Gao, Z. L. Song and J. H. Wu, Modelling triatomine bug population and Trypanosoma rangeli transmission dynamics: co-feeding, pathogenic effect and linkage with chagas disease, Math. Biosci., 2020, 324. [37] Y. C. Xu, Z. R. Zhu, Y. Yang and F. W. Meng, Vectored immunoprophylaxis and cell-to-cell transmission in HIV dynamics, Inter. J. Bifur. & Chaos, 2020, 30(13), 1–19. [38] W. J. Zhang, L. M. Wahl and P. Yu, Backward bifurcations, turning points and rich dynamics in simple disease models., J. Math. Biol., 2016, 73(4), 1–30. -
-
-
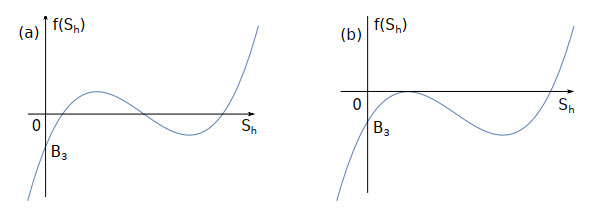
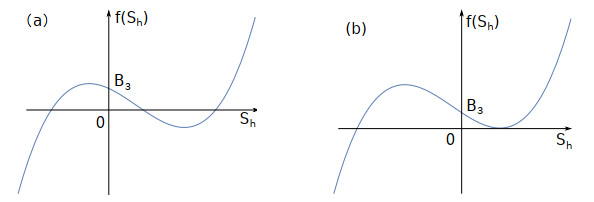
Figure 1.
The number of root for
$ f(S_{h})=0 $ $ ac\mu_{1}>d\mu_{2} $ -
Figure 2.
The number of root for
$ f(S_{h})=0 $ $ ac\mu_{1}<d\mu_{2}. $ -
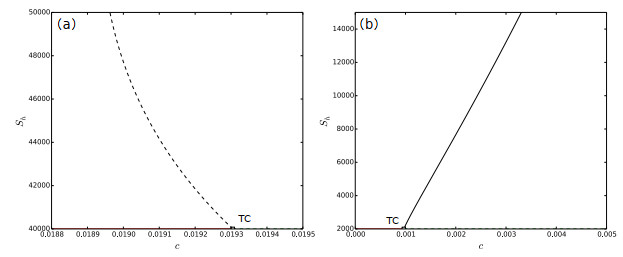
Figure 3.
(a) Backward bifurcation diagram of system (2.1) showing
$ c $ $ S_{h} $ $ \Lambda_{h}=100 $ $ c $ $ S_{h} $ $ \Lambda_{h}=5 $ -
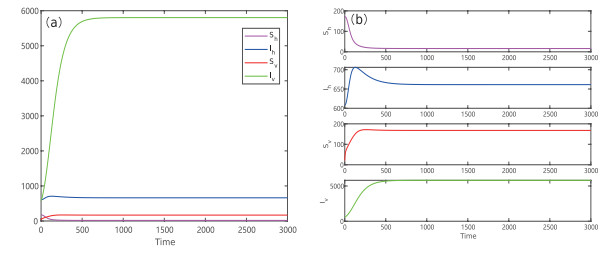
Figure 4.
Numerical solution of system (2.1) tends to a stable equilibrium when the time tends to infinity, where
$ \Lambda_{h}=5, r=0.0274, \sigma=0.0002, \mu_{1}=0.0025, \mu_{2}=0.0083, d=0.0083 $ $ (S_{h},I_{h},S_{v},I_{v})=(172,609,21,576) $ -
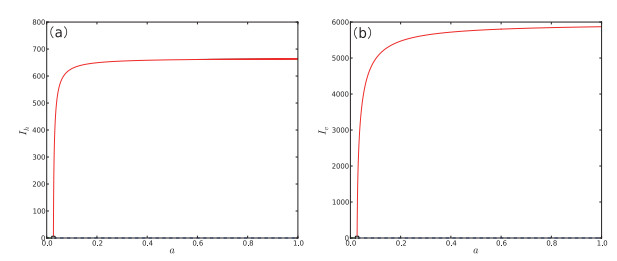
Figure 5.
One-parameter bifurcation diagram of system (2.1) with respect to
$ a. $ $ a $ $ I_{h} $ $ a $ $ I_{v} $ -
Figure 6.
One-parameter bifurcation diagram of system (2.1) with respect to
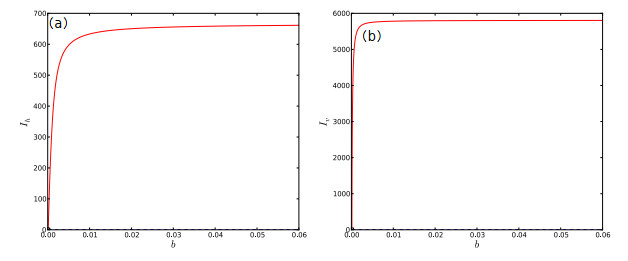
$ b. $ $ b $ $ I_{h} $ $ b $ $ I_{v} $ -
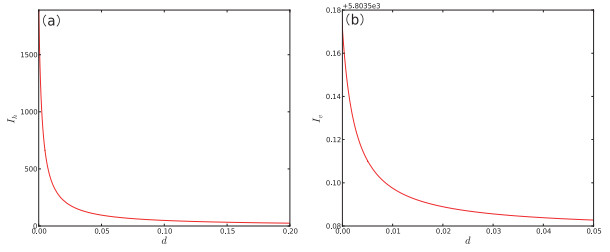
Figure 7.
(a) One-parameter bifurcation diagram of system (2.1) showing
$ d $ $ I_{h} $ $ d $ $ I_{v} $




 DownLoad:
DownLoad: