| Citation: |
Jianzhi Cao, Li Ma, Pengmiao Hao. BIFURCATION ANALYSIS IN A MODIFIED LESLIE-GOWER PREDATOR-PREY MODEL WITH BEDDINGTON-DEANGELIS FUNCTIONAL RESPONSE[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 3026-3053. doi: 10.11948/20230183
|
BIFURCATION ANALYSIS IN A MODIFIED LESLIE-GOWER PREDATOR-PREY MODEL WITH BEDDINGTON-DEANGELIS FUNCTIONAL RESPONSE
-
Abstract
This paper investigates the dynamics of a modified Leslie-Gower predator-prey model with Bedington-DeAngelis functional response. Some properties are explored, including positivity, dissipativity, permanence, and stability. In addition, the transcritical bifurcation and Hopf bifurcation taking $ d $ as the bifurcation parameter and Bogdanov-Takens bifurcation taking $ d $ and $ n $ as bifurcation parameters are studied. The theoretical results of this paper are verified by numerical simulation. The results show that the system has rich dynamical behaviors.
-
-
References
[1] N. Ali and M. Jazar, Global dynamics of a modified Leslie-Gower predator-prey model with Crowley-Martin functional responses, J. Appl. Math. Comput., 2013, 43(1–2), 271–293. doi: 10.1007/s12190-013-0663-3 [2] M. A. Aziz-Alaoui and M. D. Okiye, Boundedness and global stability for a predator-prey model with modified Leslie-Gower and Holling-type Ⅱ schemes, Appl. Math. Lett., 2003, 16(7), 1069–1075. doi: 10.1016/S0893-9659(03)90096-6 [3] J. R. Beddington, Mutual interference between parasites or predators and its effect on searching efficiency, Journal of Animal Ecology, 1975, 44,331–340. doi: 10.2307/3866 [4] S. Bentout, S. Djilali and A. Atangana, Bifurcation analysis of an age-structured prey-predator model with infection developed in prey, Math. Methods Appl. Sci., 2022, 45(3), 1189–1208. doi: 10.1002/mma.7846 [5] A. A. Berryman, The orgins and evolution of predator-prey theory, Ecology, 1992, 73(5), 1530–1535. doi: 10.2307/1940005 [6] O. Borysenko and O. Borysenko, Long-time behavior of a nonautonomous stochastic predator-prey model with jumps, Modern Stochastics: Theory and Applications, 2021, 8(1), 17–39. [7] F. Chen, On a nonlinear nonautonomous predator-prey model with diffusion and distributed delay, J. Comput. Appl. Math., 2005,180(1), 33–49. doi: 10.1016/j.cam.2004.10.001 [8] D. L. Deangelis, R. A. Goldstein and R. V. O'Neill, A model for tropic interaction, Ecology, 1975, 56(4), 881–892. doi: 10.2307/1936298 [9] M. Farshid and Y. Jalilian, Turing instability in a modified cross-diffusion Leslie-Gower predator-prey model with Beddington-DeAngelis functional response, Bound. Value Probl., 2022, 2022(1), 1–20. doi: 10.1186/s13661-021-01582-x [10] J. Huang, Y. Gong and J. Chen, Multiple bifurcations in a predator-prey system of Holling and Leslie Type with constant-yield prey harvesting, Internat. J. Bifur. Chaos, 2013, 23(10), 1350164. doi: 10.1142/S0218127413501642 [11] X. C. Huang, Stability of a general predator-prey model, J. Franklin Inst., 1990,327(5), 751–769. doi: 10.1016/0016-0032(90)90081-S [12] P. H. Leslie and J. C. Gower, The properties of a stochastic model for the predator-prey type of interaction between two species, Biometrika, 1960, 47(3), 219–234. [13] C. Liu, S. Li and Y. Yan, Hopf bifurcation analysis of a density predator-prey model with Crowley-Martin functional response and two time delays, J. Appl. Anal. Comput., 2019, 9(4), 1589–1605. [14] P. Liu and B. Yang, Dynamics analysis of a reaction-diffusion system with Beddington-DeAngelis functional response and strong Allee effect, Nonlinear Anal. Real World Appl., 2020, 51, 102953. doi: 10.1016/j.nonrwa.2019.06.003 [15] X. Liu, T. Zhang, X. Meng et al., Turing-Hopf bifurcations in a predator-prey model with herd behavior, quadratic mortality and prey-taxis, Phys. A, 2018,496,446–460. doi: 10.1016/j.physa.2018.01.006 [16] A. Lotka, Elements of Physical Biology, Williams and Wilkins, Baltimore, 1925. [17] Z. Ma, F. Chen and C. Wu, Dynamic behaviors of a Lotka-Volterra predator-prey model incorporating a prey refuge and predator mutual interference, Appl. Math. Comput., 2013,219(15), 7945–7953. [18] P. Majumdar, B. Mondal, S. Debnath et al., Effect of fear and delay on a prey-predator model with predator harvesting, Comput. Appl. Math., 2022, 41(8), 357. doi: 10.1007/s40314-022-02066-z [19] B. T. Mulugeta, L. Yu, Q. Yuan et al., Bifurcation analysis of a predator-prey model with strong Allee effect and Beddington-DeAngelis functional response, Discrete Contin. Dyn. Syst. Ser. B, 2023, 28(3), 1938–1963. doi: 10.3934/dcdsb.2022153 [20] L. Perko, Differential Equations and Dynamical Systems, Springer Verlag, 2001. [21] M. L. Rosenzweig and R. H. MacArthur, Graphical representation and stability conditions of predator-prey interactions, Am. Naturalist, 1963, 97(895), 209–223. doi: 10.1086/282272 [22] Y. Takeuchi, Global dynamical properties of Lotka-Volterra systems, World Scientific, 1996. [23] J. P. Tripathi, S. S. Meghwani, M. Thakur et al., A modified Leslie-Gower predator-prey interaction model and parameter identifiability, Commun. Nonlinear Sci. Numer. Simul., 2018, 54,331–346. doi: 10.1016/j.cnsns.2017.06.005 [24] V. Volterra, Fluctuations in the abundance of a species considered mathematically, Nature, 1926,118(2972), 558–560. doi: 10.1038/118558a0 [25] Z. Zhang, T. Ding, W. Huang et al., Qualitative Theory of Differential Equations, Science Press, 1992. -
-
Figures(4)
Export File
Citation
Jianzhi Cao, Li Ma, Pengmiao Hao. BIFURCATION ANALYSIS IN A MODIFIED LESLIE-GOWER PREDATOR-PREY MODEL WITH BEDDINGTON-DEANGELIS FUNCTIONAL RESPONSE[J]. Journal of Applied Analysis & Computation, 2023, 13(5): 3026-3053. doi: 10.11948/20230183
Format
Content
DownLoad:
-
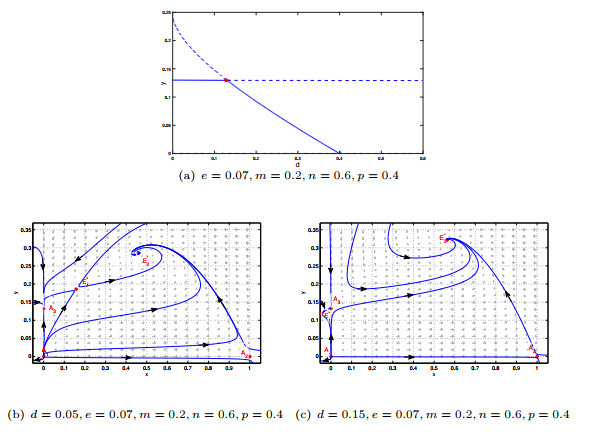
Figure 1.
Number of positive equilibrium under parameter conditions.
-
Figure 2.
(a) the transcritical bifurcation diagram around
$ A_{3}(0, \frac{mp}{n}) $ $ e=0.07, m=0.2, n=0.6, p=0.4 $ $ d=0.05 $ $ d=0.15 $ -
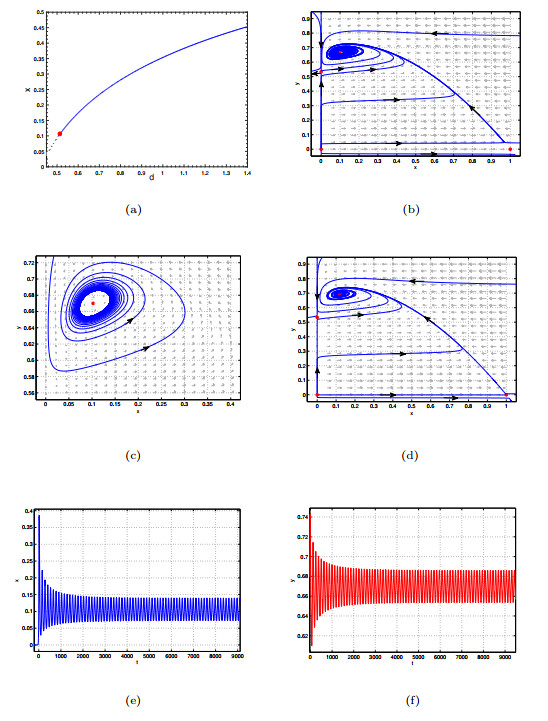
Figure 3.
(a) Hopf bifurcation around
$ E^*(0.10978, 0.6797) $ $ e=0.2, m=0.02, n=0.015, p=0.4 $ $ d=0.53 $ $ d=0.51 $ -
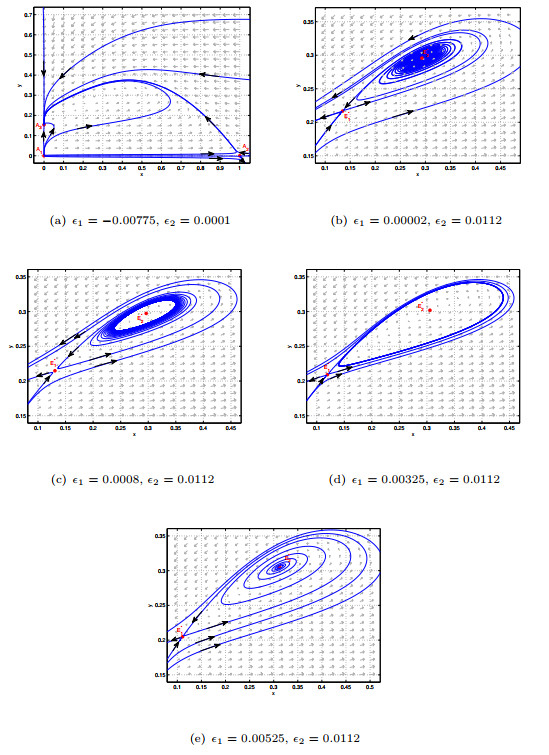
Figure 4.
Phase diagram near Bogdanov-Takens bifurcation point when
$ d_{BT}=0.08975, e=0.12, m=0.2, n_{BT}=0.3899, p=0.3 $ $ (\epsilon_{1}, \epsilon_{2})=(-0.00775, 0.0001) $ $ (\epsilon_{1}, \epsilon_{2})=(0.00002, 0.0112) $ $ (\epsilon_{1}, \epsilon_{2})=(0.0008, 0.0112) $ $ (\epsilon_{1}, \epsilon_{2})=(0.00325, 0.0112) $ $ (\epsilon_{1}, \epsilon_{2})=(0.00525, 0.0112) $