| Citation: |
Jing Jiang, Yixian Gao, Weipeng Zhang, Lan Yin. BIFURCATION OF TRAVELING WAVE SOLUTIONS OF THE $K(M, N)$ EQUATION WITH GENERALIZED EVOLUTION TERM[J]. Journal of Applied Analysis & Computation, 2019, 9(3): 853-863. doi: 10.11948/2156-907X.20180035
|
BIFURCATION OF TRAVELING WAVE SOLUTIONS OF THE $K(M, N)$ EQUATION WITH GENERALIZED EVOLUTION TERM
-
Abstract
In this paper, by using bifurcation theory and methods of plane dynamic system, we investigate the bifurcations of the traveling wave system corresponding to the $K(m, n)$ equation with generalized evolution term. Under different parameter conditions, some exact explicit parametric representations of traveling wave solution are obtained. -
-
References
[1] A. Biswas, 1-soliton solution of the $K(m, n)$ equation with generalized evolution, Phys. Lett. A, 2008, 372(25), 4601-4602. doi: 10.1016/j.physleta.2008.05.002 CrossRef $K(m, n)$ equation with generalized evolution" target="_blank">Google Scholar
[2] P. F. Byrd and M. D. Fridman, Handbook of Elliptic Integrals For Engineers and Scientists, Springer, Berlin, 1971. [3] A. Y. Chen and J. B. Li, Single peak solitary wave solutions for the osmosis $K(2, 2)$ equation under inhomogeneous boundary condition, J. Math. Anal. Appl., 2010, 369(2), 758-766. doi: 10.1016/j.jmaa.2010.04.018 CrossRef $K(2, 2)$ equation under inhomogeneous boundary condition" target="_blank">Google Scholar
[4] Y. G. Fu and J. B. Li, Exact stationary-wave solutions in the standard model of the Kerr-nonlinear optical fiber with the Bragg grating, J. Appl. Anal. Comput., 2017, 7(3), 1177-1184. [5] M. A. Han, L. J. Zhang, Y. Wang and C. M. Khalique, The effects of the singular lines on the traveling wave solutions of modified dispersive water wave equations, Nonlinear Anal. Real World Appl., 2019, 47, 236-250. doi: 10.1016/j.nonrwa.2018.10.012 [6] T. L. He, Bifurcation of traveling wave solutions of (2+1) dimensional Konopelchenko-Dubrovsky equations, Appl. Math. Comput., 2008, 204(2), 773-783. [7] T. D. Leta and J. B. Li, Existence of kink and unbounded traveling wave solutions of the Casimir equation for the Ito system, J. Appl. Anal. Comput., 2017, 7(2), 632-643. [8] J. B. Li, Dynamical understanding of loop soliton solutions for several nonlinear wave equations, Sci. China Ser. A, 2007, 50(6), 773-785. doi: 10.1007/s11425-007-0039-y [9] J. B. Li, Exact explicit peakon and periodic cusp wave solutions for several nonlinear wave equation, J. Dyn. Diff. Equ., 2008, 20(4), 909-922. doi: 10.1007/s10884-008-9114-5 [10] J. B. Li, Notes on exact travelling wave solutions for a long wave-short wave mode, J. Appl. Anal. Comput., 2015, 5(1), 138-140. [11] J. B. Li and H. H. Dai, On the study of singular nonlinear traveling wave equations: dynamical system approach, Science Press, Beijing, 2007. [12] J. B. Li and Z. R. Liu, Smooth and non-smooth traveling waves in an nonlinearly dispersive equation, Appl. Math. Model., 2000, 25(1), 41-56. [13] J. B. Li and Z. R. Liu, Traveling wave solutions for a class of nonlinear dispersive equations, China. Ann. Math. B, 2002, 23(3), 397-418. doi: 10.1142/S0252959902000365 [14] J. B. Li and J. W. Shen, Traveling wave solutions in a model of the helix polypeptide chains, Chaos, Soliton and Fractals, 2004, 20(4), 827-841. doi: 10.1016/j.chaos.2003.09.007 [15] J. B. Li and J. X. Zhang, Bifurcations of traveling wave solutions for the generalization form of the modified KdV equation, Chaos, Soliton and Fractals, 2004, 21(4), 899-913. doi: 10.1016/j.chaos.2003.12.026 [16] J. B. Li and Y. Zhang, Exact M/W-shape solitary wave solution determined by a singular traveling wave equation, Nonlinear Anal. Real World Appl., 2009, 10(3), 1797-1802. doi: 10.1016/j.nonrwa.2008.02.016 [17] J. B. Li and J. Q. Zhi, Explicit soliton solutions of the Kaup-Kupershmidt equation through the dynamical system approach, J. Appl. Anal. Comput., 2011, 1(2), 243-250. [18] P. Rosenau, On nonanalytic solitary waves formed by a nonlinear dispersion, Phys. Lett. A, 1997, 230, 305-318. doi: 10.1016/S0375-9601(97)00241-7 [19] P. Rosenau and J.M. Hyman, Compacton: solitons with finite wavelength, Phys. Rev. Lett., 1993, 70(5), 564-567. doi: 10.1103/PhysRevLett.70.564 [20] S. Q. Tang and M. Li, Bifurcations of traveling wave solutions in a class of generalized KdV equation, Appl. Math. Comput., 2006, 177(2), 589-596. [21] H. Triki and A. M. Wazwaz, Soliton solutions for (2+1)-dimensional and (3+1)-dimensional $K(m, n)$ equation, Appl. Math. Comput., 2009, 217(4), 1733-1740. [22] C. H. Xu and L. X. Tian, The bifurcation and peakon for $K(2, 2)$ equation with osmosis dispersion, Chaos, Soliton and Fractals, 2009, 40(2), 893-901. doi: 10.1016/j.chaos.2007.08.042 CrossRef $K(2, 2)$ equation with osmosis dispersion" target="_blank">Google Scholar
[23] L. J. Zhang, H. X. Chang and C. M. Khalique, Sub-manifold and traveling wave solutions of Ito's 5th-order mKdV equation, J. Appl. Anal. Comput., 2017, 7(4), 1417-1430. [24] L. J. Zhang and C. M. Khalique, Exact solitary wave and periodic wave solutions of the Kaup-Kuperschmidt equation, J. Appl. Anal. Comput., 2015, 5(3), 485-495. [25] L. J. Zhang and C. M. Khalique, Classification and bifurcation of a class of second-order ODEs and its application to nonlinear PDEs, Discrete Contin. Dyn. Syst. Ser., 2018, 11(4), 777-790. [26] L. J. Zhang, Y. Wang, C. M. Khalique and Y. Z. Bai, Peakon and cuspon solutions of a generalized Camassa-Holm-Novikov equation, J. Appl. Anal. Comput., 2018, 8(6), 1938-1958. -
-
Figures(6)
Export File
Citation
Jing Jiang, Yixian Gao, Weipeng Zhang, Lan Yin. BIFURCATION OF TRAVELING WAVE SOLUTIONS OF THE $K(M, N)$ EQUATION WITH GENERALIZED EVOLUTION TERM[J]. Journal of Applied Analysis & Computation, 2019, 9(3): 853-863. doi: 10.11948/2156-907X.20180035
Format
Content
DownLoad:
-
Figure 1.
$(g, c)$ -plane, where$L_{1}=L_1^+\cup L_1^-:g=0$ ,$L_{2}^{+}:c=\sqrt{-ag} ~(g < 0)$ . -
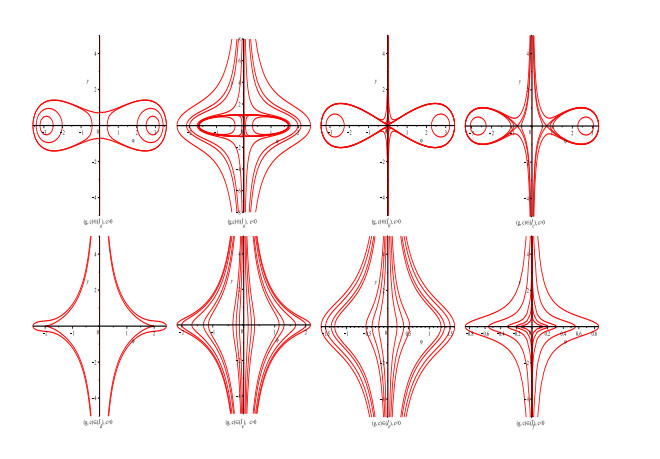
Figure 2. The phase portrait bifurcation of system (2.4) when
$a>0$ . -
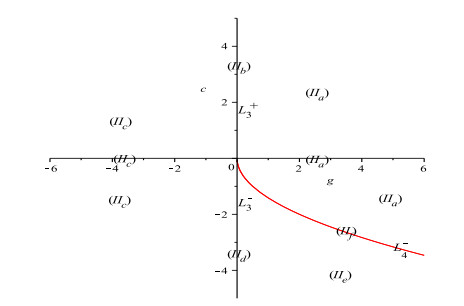
Figure 3.
$(g, c)$ -plane, where$L_{1}=L_3^+\cup L_3^-:g=0$ ,$L_{4}^{-}:c=-\sqrt{-ag} ~(g < 0)$ . -
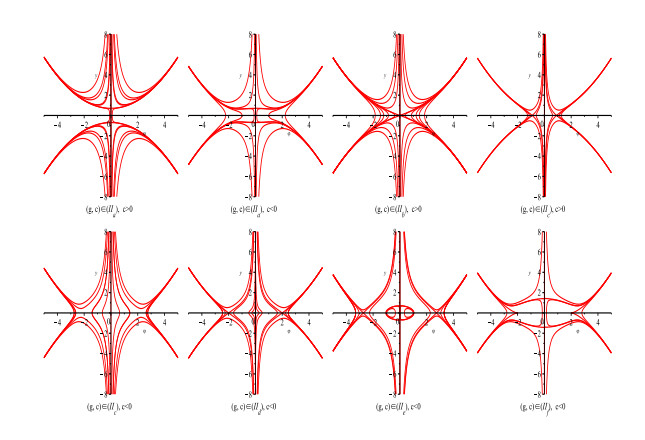
Figure 4. The phase portrait bifurcation of system (2.4) when
$a < 0$ . - Figure 5. The smooth periodic wave solution of the equation (3.2) with a=1, b=2, c=-4, g=1.
- Figure 6. The smooth periodic wave solution of the equation (3.3) when a=1, b=2, c=-4, g=1.