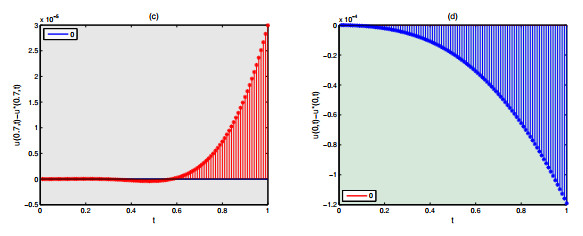
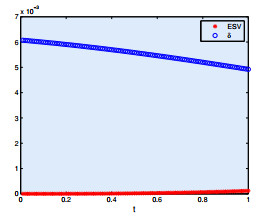
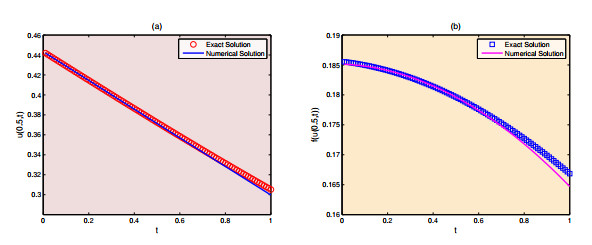
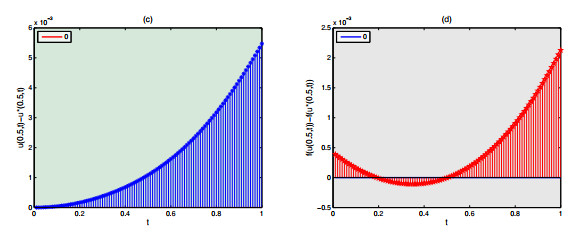
|
[1]
|
M. Abtahi, R. Pourgholi and A. Shidfar, Existence and uniqueness of solution for a two dimensional nonlinear inverse diffusion problem, Nonlinear Analysis: Theory, Methods & Applications, 2011, 74(7), 2462-2467.
Google Scholar
|
|
[2]
|
O. M. Alifanov, Inverse Heat Transfer Problems, Springer, NewYork, 1994.
Google Scholar
|
|
[3]
|
A. J. Ammerman and L. L. Cavalli-Sforza, The Neolithic Transition and the Genetics of Population in Europe, Princeton University Press, 1984.
Google Scholar
|
|
[4]
|
J. V. Beck, B. Blackwell and C. R. St. Clair, Inverse Heat Conduction: IllPosed Problems, Wiley-Interscience, NewYork, 1985.
Google Scholar
|
|
[5]
|
J. V. Beck and D. C. Murio, Combined function specification-regularization procedure for solution of inverse heat condition problem, AIAA J., 1986, 24(1), 180-185. doi: 10.2514/3.9240
CrossRef Google Scholar
|
|
[6]
|
J. M. G Cabeza, J. A. M Garcia and A. C. Rodriguez, A Sequential Algorithm of Inverse Heat Conduction Problems Using Singular Value Decomposition, International Journal of Thermal Sciences, 2005, 44(3), 235-244. doi: 10.1016/j.ijthermalsci.2004.06.009
CrossRef Google Scholar
|
|
[7]
|
C. F. Chen and C. H. Hsiao, Haar wavelet method for solving lumped and distributed-parameter systems, IEE Proc.: part D, 1997, 144(1), 87-94.
Google Scholar
|
|
[8]
|
L. Elden, A Note on the Computation of the Generalized Cross-validation Function for Ill-conditioned Least Squares Problems, BIT, 1984, 24(4), 467-472. doi: 10.1007/BF01934905
CrossRef Google Scholar
|
|
[9]
|
E. S. Fahmy, Travelling wave solution for some time-delayed equations through factorizations, Chaos Solitions Fract., 2008, 38(4), 1209-1216.
Google Scholar
|
|
[10]
|
S. Foadian, R. Pourgholi and S. Hashem Tabasi, Cubic B-spline method for the solution of an inverse parabolic system, Applicable Analysis, 2018, 97(3), 438-465. doi: 10.1080/00036811.2016.1272102
CrossRef Google Scholar
|
|
[11]
|
P. K. Galenko and D. A. Danilov, Selection of the dynamically stable regime of rapid solidification front motion in an isothermal binary alloy, J. Cryst. Growth, 2000, 216(1-4), 512-536. doi: 10.1016/S0022-0248(00)00338-9
CrossRef Google Scholar
|
|
[12]
|
G. H. Golub, M. Heath and G. Wahba, Generalized Cross-validation as a Method for Choosing a Good Ridge Parameter, Technometrics, 1979, 21(2), 215-223. doi: 10.1080/00401706.1979.10489751
CrossRef Google Scholar
|
|
[13]
|
A. Haar, Zur theorie der orthogonalen Funktionsysteme, Math. Annal., 1910, 69, 331-371. doi: 10.1007/BF01456326
CrossRef Google Scholar
|
|
[14]
|
P. C. Hansen, Analysis of discrete ill-posed problems by means of the L-curve, SIAM Rev., 1992, 34(4), 561-80. doi: 10.1137/1034115
CrossRef Google Scholar
|
|
[15]
|
G. Hariharan, K. Kannan and K. R. Sharma, Haar wavelet method for solving Fisher's equation, Applied Mathematics and Computation, 2009, 211(2), 284-292. doi: 10.1016/j.amc.2008.12.089
CrossRef Google Scholar
|
|
[16]
|
C. H. Hsiao and W. J. Wang, Haar wavelet approach to nonlinear stiff systems, Math. Comput. Simul., 2001, 57(6), 347-353. doi: 10.1016/S0378-4754(01)00275-0
CrossRef Google Scholar
|
|
[17]
|
C. H. Huang and Y. L. Tsai, A transient 3-D inverse problem in imaging the time-dependentlocal heat transfer coefficients for plate fin, Applied Therma Engineering, 2005, 25(14-15), 2478-2495. doi: 10.1016/j.applthermaleng.2004.12.003
CrossRef Google Scholar
|
|
[18]
|
R. Kalpana and S. R. Balachandar, Haar wavelet method for the analysis of transistor circuits, Int. J. Electron. Commun. (AEU), 2007, 61(9), 589-594. doi: 10.1016/j.aeue.2006.10.003
CrossRef Google Scholar
|
|
[19]
|
C. L. Lawson and R. J. Hanson, Solving Least Squares Problems, Philadelphia, PA: SIAM, 1995.
Google Scholar
|
|
[20]
|
L. Martin, L. Elliott, P. J. Heggs, D. B. Ingham, D. Lesnic and X. Wen, Dual Reciprocity Boundary Element Method Solution of the Cauchy Problem for Helmholtz-type Equations with Variable Coefficients, Journal of sound and vibration, 2006, 297(1-2), 89-105. doi: 10.1016/j.jsv.2006.03.045
CrossRef Google Scholar
|
|
[21]
|
H. Molhem and R. Pourgholi, A numerical algorithm for solving a one-dimensional inverse heat conduction problem, Journal of Mathematics and Statistics, 2008, 4(1), 60-63.
Google Scholar
|
|
[22]
|
D. C. Murio and J. R. Paloschi, Combined mollification-future temperature procedure for solution of inverse heat conduction problem, J. comput. Appl. Math., 1988, 23(2), 235-244. doi: 10.1016/0377-0427(88)90282-8
CrossRef Google Scholar
|
|
[23]
|
D. A. Murio, The Mollification Method and the Numerical Solution of Ill-Posed Problems, Wiley-Interscience, NewYork, 1993.
Google Scholar
|
|
[24]
|
S. Rendine, A. Piazza and L. L. Cavalli-Sforza, Simulation and separation by principle components of multiple demic expansions in Europe, Am. Nat., 1986, 128(5), 681-706. doi: 10.1086/284597
CrossRef Google Scholar
|
|
[25]
|
R. Pourgholi, H. Dana and S. H. Tabasi, Solving an inverse heat conduction problem using genetic algorithm: Sequential and multi-core parallelization approach, Applied Mathematical Modelling, 2014, 38(7-8), 1948-1958. doi: 10.1016/j.apm.2013.10.019
CrossRef Google Scholar
|
|
[26]
|
R. Pourgholi, A. Esfahani, S. Foadian and S. Parehkar, Resolution of an inverse problem by Haar basis and Legendre wavelet methods, IJWMIP., 2013, 11(05), 1350034 (21 pages).
Google Scholar
|
|
[27]
|
R. Pourgholi, S. Foadian and A. Esfahani, Haar basis method to solve some inverse problems for two-dimensional parabolic and hyperbolic equations, TWMS J. App. Eng. Math., 2013, 3(1), 10-32.
Google Scholar
|
|
[28]
|
R. Pourgholi, M. Rostamian and M. Emamjome, A numerical method for solving a nonlinear inverse parabolic problem, Inverse Problems in Science and Engineering, 2010, 18(8), 1151-1164. doi: 10.1080/17415977.2010.518287
CrossRef Google Scholar
|
|
[29]
|
R. Pourgholi, N. Tavallaie and S. Foadian, Applications of Haar basis method for solving some ill-posed inverse problems, J. Math. Chem., 2012, 50(8), 2317-2337. doi: 10.1007/s10910-012-0036-4
CrossRef Google Scholar
|
|
[30]
|
A. N. Tikhonov and V. Y. Arsenin, On the solution of ill-posed problems, New York, Wiley, 1977.
Google Scholar
|
|
[31]
|
A. N. Tikhonov and V. Y. Arsenin, Solution of Ill-Posed Problems, V.H. Winston and Sons, Washington, DC, 1977.
Google Scholar
|
|
[32]
|
X. Y. Wang and Y. K. Lu, Exact solutions of the extended Burgers-Fisher equation, Chinese Phys. Lett., 1990, 7(4), 145-147. doi: 10.1088/0256-307X/7/4/001
CrossRef Google Scholar
|
|
[33]
|
J. Zhang, P. Wei and M. Wang, The investigation into the exact solutions of the generalized time-delayed Burgers-Fisher equation with positive fractional power terms, Applied Mathematical Modelling, 2012, 36(5), 2192-2196. doi: 10.1016/j.apm.2011.08.004
CrossRef Google Scholar
|
|
[34]
|
J. Zhou, Y. Zhang, J. K. Chen and Z. C. Feng, Inverse Heat Conduction in a Composite Slab With Pyrolysis Effect and Temperature-Dependent Thermophysical Properties, J. Heat Transfer, 2010, 132(3), 034502 (3 pages).
Google Scholar
|




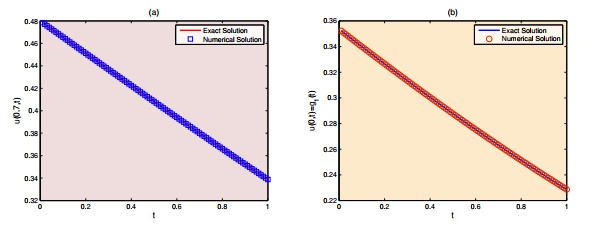

 DownLoad:
DownLoad: