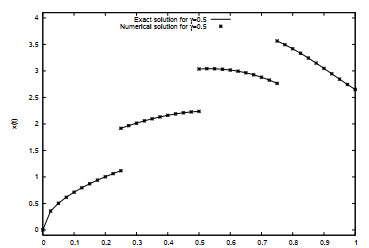
|
[1]
|
J. Cao and C. Xu, A high order schema for the numerical solution of the fractional ordinary differential equations, J. Comput. Phys., 2013, 238, 154-168. doi: 10.1016/j.jcp.2012.12.013
CrossRef Google Scholar
|
|
[2]
|
K. Diethelm and N. J. Ford, Analysis of fractional differential equations, J. Math. Anal. Appl., 2002, 265(2), 229-248.
Google Scholar
|
|
[3]
|
J. Dixon and S. McKee, Weakly singular discrete Gronwall inequalities, Z. Angew. Math. Mech., 1986, 66(11), 535-544. doi: 10.1002/zamm.19860661107
CrossRef Google Scholar
|
|
[4]
|
M. Fečkan, Y. Zhou and J. Wang, On the concept and existence of solution for impulsive fractional differential equations, Commun. Nonlinear Sci. Numer. Simul., 2012, 17(7), 3050-3060. doi: 10.1016/j.cnsns.2011.11.017
CrossRef Google Scholar
|
|
[5]
|
G. Gao and Z. Zun, Two alternating direction implicit difference schemes for two-dimensional distributed-order fractional diffusion equations, J. Sci. Comput., 2016, 66, 1281-1312. doi: 10.1007/s10915-015-0064-x
CrossRef Google Scholar
|
|
[6]
|
T. Guo and K. Zhang, Impulsive fractional partial differential equations, Appl. Math. Comput., 2015, 257, 581-590.
Google Scholar
|
|
[7]
|
R. Hilfer, Applications of Fractional Calculus in Physics, World Scientific, Singapore, 2000.
Google Scholar
|
|
[8]
|
J. Huang, Y. Tang and L. Vázquez, Convergence analysis of a block-by-block method for fractional differential equations, Numer. Math. Theory Methods Appl., 2012, 5(2), 229-241. doi: 10.4208/nmtma.2012.m1038
CrossRef Google Scholar
|
|
[9]
|
P. Kumar, D. Pandey and D. Bahuguna, On a new class of abstract impulsive functional differential equations of fractional order, J. Nonlinear Sci. Appl., 2014, 7, 102-114. doi: 10.22436/jnsa.007.02.04
CrossRef Google Scholar
|
|
[10]
|
P. Kumar and O. Agrawal, An approximate method for numerical solution of fractional differential equations, Signal Process., 2006, 86(10), 2602-2610. doi: 10.1016/j.sigpro.2006.02.007
CrossRef Google Scholar
|
|
[11]
|
Z. Lin, J. Wang and W. Wei, Multipoint BVPs for generalized impulsive fractional differential equations, Appl. Math. Comput., 2015, 258, 608-616.
Google Scholar
|
|
[12]
|
P. Linz, An method for nonlinear solving Volterra integral equations of the second kind, Math. Comput., 1969, 23(107), 595-599. doi: 10.1090/S0025-5718-1969-0247794-7
CrossRef Google Scholar
|
|
[13]
|
C. Lubich, Fractional linear multistep methods for Abel-Volterra integral equations of the second kind, Math. Comput., 1985, 45(172), 463-469. doi: 10.1090/S0025-5718-1985-0804935-7
CrossRef Google Scholar
|
|
[14]
|
K.S. Miller and B. Ross, An Introduction to the Fractional Calculus and Fractional Differential Equations, Wiley-Interscience, New York, 1993.
Google Scholar
|
|
[15]
|
N. Nyamoradi and R. Rodríguez-López, On boundary value problems for impulsive fractional differential equations, Appl. Math. Comput., 2015, 271, 874-892.
Google Scholar
|
|
[16]
|
I. Podlubny, Fractional Differential Equations, Acad. Press, New York, 1999.
Google Scholar
|
|
[17]
|
Z. Wang and J. Cao, Optimal convergence order analysis of a block-by-block algorithm for fractional differential equations, Chinese J. Engrg. Math., 2015, 32(4), 533-545.
Google Scholar
|
|
[18]
|
J. Wang, M. Fečkan and Y. Zhou, Relaxed controls for nonlinear fractional impulsive evolution equations, J. Optim. Theory Appl., 2013, 156(1), 13-32.
Google Scholar
|
|
[19]
|
A. Young, The application of approximate product-integration to the numerical solution of integral equations, Proc. R. Soc. London Ser. A, 1954, 224(1159), 561-573. doi: 10.1098/rspa.1954.0180
CrossRef Google Scholar
|




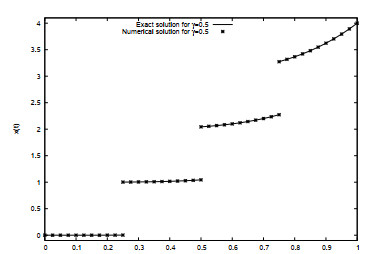

 DownLoad:
DownLoad: