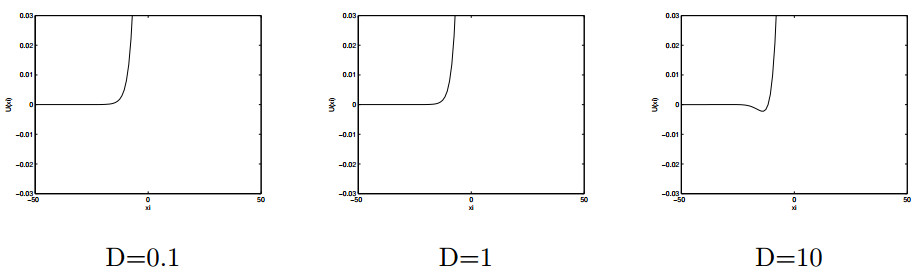
|
[1]
|
B. Batiha, M. Noorani, I. Hashim, Application of variational iteration method to the generalized Burgers-Huxley equation, Chaos Solitons Fractals, 2008, 36, 660-663. doi: 10.1016/j.chaos.2006.06.080
CrossRef Google Scholar
|
|
[2]
|
W. Beyn, The numerical computation of connecting orbits in dynamical systems, IMA J. Numer. Anal., 1990, 10, 379-405. doi: 10.1093/imanum/10.3.379
CrossRef Google Scholar
|
|
[3]
|
D. Cohen, J. Murray, A generalised diffusion model for growth and dispersal in a population, J. Math. Biol., 1981, 12, 237-249. doi: 10.1007/BF00276132
CrossRef Google Scholar
|
|
[4]
|
M. Darvishi, S. Kheybari, F. Khani, Spectral collocation method and Darvishi's preconditionings to solve the generalized Burgers-Huxley equation, Commun. Nonlinear Sci. Numer. Simulat. 2008, 13, 2091-2103. doi: 10.1016/j.cnsns.2007.05.023
CrossRef Google Scholar
|
|
[5]
|
X. Deng, Travelling wave solutions for the generalized Burgers-Huxley equation, Appl. Math. Comput., 2008, 204, 733-737.
Google Scholar
|
|
[6]
|
E. Fan, Extended tanh-function method and its applications to nonlinear equations, Phys. Lett. A, 2000, 277, 212-218. doi: 10.1016/S0375-9601(00)00725-8
CrossRef Google Scholar
|
|
[7]
|
N. Fenichel, Geometric singular perturbation theory for ordinary differential equations, J. Differential Equations, 1979, 31, 53-98. doi: 10.1016/0022-0396(79)90152-9
CrossRef Google Scholar
|
|
[8]
|
R. Fitzhugh, Mathematical models of excitation and propagation in nerve, in: H.P. Schwan (Ed.), Biological Engineering, McGraw-Hill, New York, 1969, 1-85.
Google Scholar
|
|
[9]
|
Y. Fu, J. Li, Exact stationary-wave solutions in the standard model of the KerrNonlinear optical fiber with the Bragg grating, J. Appl. Anal. Comput., 2017, 7(3), 1177-1184.
Google Scholar
|
|
[10]
|
H. Gao, R. Zhao, New exact solutions to the generalized Burgers-Huxley equation, Appl. Math. Comput., 2010, 217, 1598-1603.
Google Scholar
|
|
[11]
|
I. Hashim, M. Noorani, M. Al-Hadidi, Solving the generalized Burgers-Huxley equation using the Adomian decomposition method, Math. Comput. Model. 2006, 43, 1404-1411. doi: 10.1016/j.mcm.2005.08.017
CrossRef Google Scholar
|
|
[12]
|
F. Hoog, R. Weiss, An approximation theory for boundary value problems on infinite intervals, Computing, 1980, 24, 227-239. doi: 10.1007/BF02281727
CrossRef Google Scholar
|
|
[13]
|
M. Javidi, A numerical solution of the generalized Burger's-Huxley equation by pseudospectral method and Darvishi's preconditioning, Appl. Math. Comput. 2006, 175, 1619-1628.
Google Scholar
|
|
[14]
|
C. Jones, Geometric Singular Perturbaton Theory, in: L. Arnold, R. Johnson (Eds), CIME Lectures on Dynamical Systems, Lecture Notes in Mathematics, vol. 1, Springer-Verlag, New York, 1995.
Google Scholar
|
|
[15]
|
A. Khattak, A computational meshless method for the generalized Burger'sHuxley equation, Appl. Math. Model. 2009, 33, 3718-3729. doi: 10.1016/j.apm.2008.12.010
CrossRef Google Scholar
|
|
[16]
|
Y. Kyrychko, M. Bartuccelli, K. Blyuss, Persistence of travelling wave solutions of a fourth order diffusion system, J. Comput. Appl. Math., 2005, 176, 433-443. doi: 10.1016/j.cam.2004.07.028
CrossRef Google Scholar
|
|
[17]
|
H. Lan, K. Wang, Exact solutions for two nonlinear equations: Ⅰ, J. Phys. A: Math. Gen., 1990, 23, 3923-3928. doi: 10.1088/0305-4470/23/17/021
CrossRef Google Scholar
|
|
[18]
|
J. Li, Notes on exact travelling wave solutions for a long wave-short wave model, J. Appl. Anal. Comput. 2015, 5(1), 138-140.
Google Scholar
|
|
[19]
|
H. Liu, J. Li, Q. Zhang, Lie symmetry analysis and exact explicit solutions for general Burgers¡¯ equation, J. Comput. Appl. Math., 2009, 228, 1-9. doi: 10.1016/j.cam.2008.06.009
CrossRef Google Scholar
|
|
[20]
|
J. Satsuma, Topics in soliton theory and exactly solvable nonlinear equations, World Scientific, Singapore, 1987.
Google Scholar
|
|
[21]
|
L. Shampine, I. Gladwell, S. Thompson, Solving ODEs with MATLAB, Cambridge University Press, 2003.
Google Scholar
|
|
[22]
|
X. Wang, Z. Zhu, Y. Lu, Solitary wave solutions of the generalized BurgersHuxley equation, J. Phys. A, 1990, 23, 271-274. doi: 10.1088/0305-4470/23/3/011
CrossRef Google Scholar
|
|
[23]
|
A.I. Volpert, V.A. Volpert, Traveling wave solutions of parabolic systems, in : Translations of Mathematical Monographs, Amer. Math. Soc.£¬ Providence, RhodeIsland, 1994.
Google Scholar
|




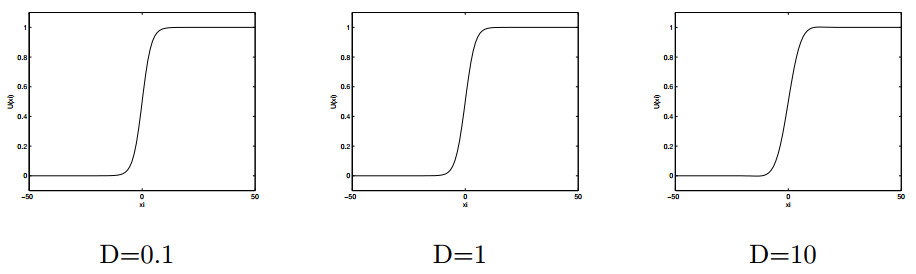

 DownLoad:
DownLoad: