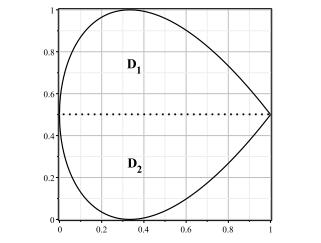
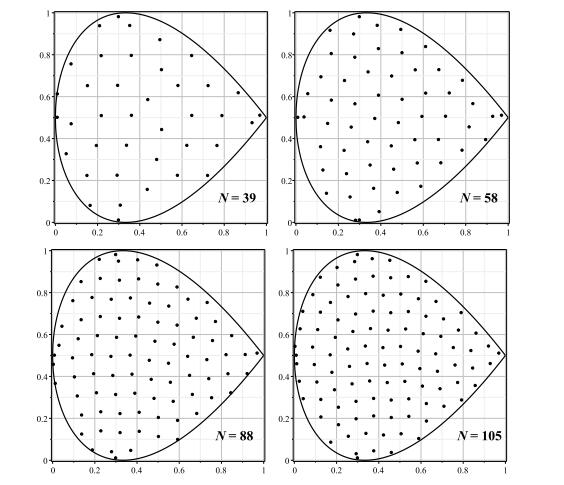
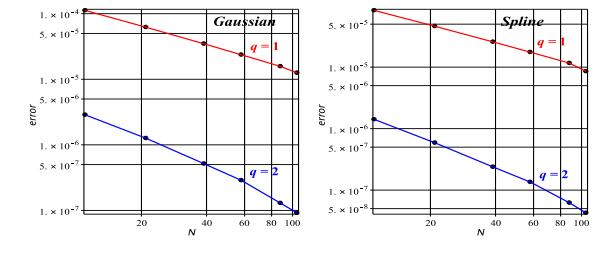
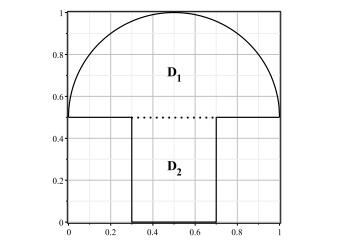
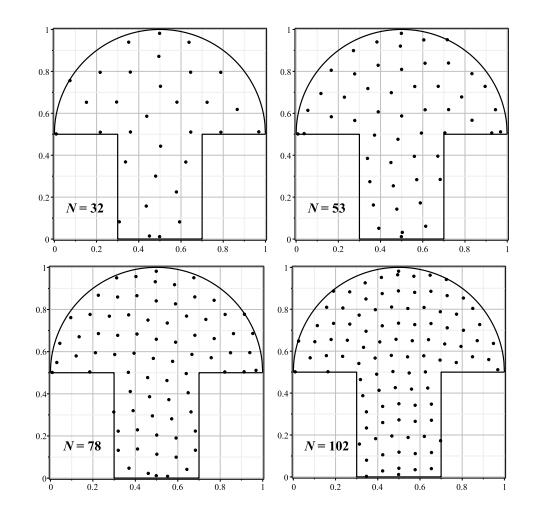
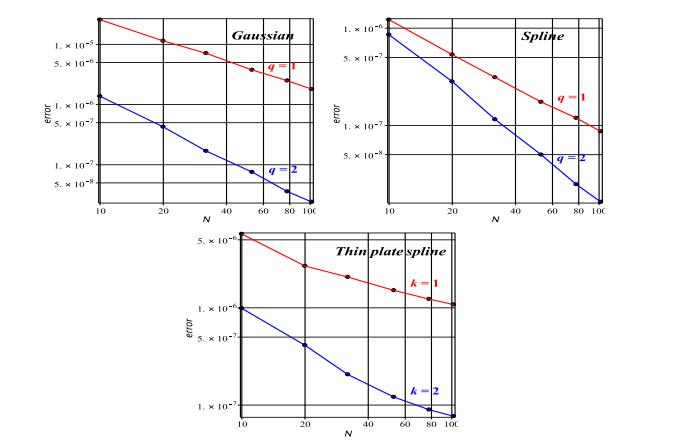
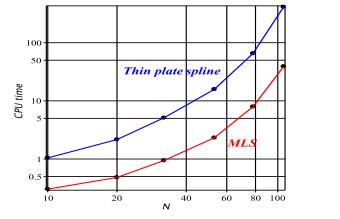
|
[1]
|
M. A. Abdou, A. A. Badr and M. B. Soliman, On a method for solving a two-dimensional nonlinear integral equation of the second kind, J. Comput. Appl. Math., 2011, 235(12), 3589-3598. doi: 10.1016/j.cam.2011.02.016
CrossRef Google Scholar
|
|
[2]
|
H. Adibi and P. Assari, On the numerical solution of weakly singular Fredholm integral equations of the second kind using Legendre wavelets, J. Vib. Control., 2011, 17(5), 689-698.
Google Scholar
|
|
[3]
|
A. Alipanah and S. Esmaeili, Numerical solution of the two-dimensional Fredholm integral equations using Gaussian radial basis function, J. Comput. Appl. Math., 2011, 235(18), 5342-5347. doi: 10.1016/j.cam.2009.11.053
CrossRef Google Scholar
|
|
[4]
|
M. G. Armentano, Error estimates in Sobolev spaces for moving least square approximations, SIAM J. Numer. Anal., 2002, 39(1), 38-51.
Google Scholar
|
|
[5]
|
M. G. Armentano and R. G. Duron, Error estimates for moving least square approximations, Appl. Numer. Math., 2001, 37(3), 397-416. doi: 10.1016/S0168-9274(00)00054-4
CrossRef Google Scholar
|
|
[6]
|
P. Assari, H. Adibi and M. Dehghan, A meshless method for solving nonlinear two-dimensional integral equations of the second kind on non-rectangular domains using radial basis functions with error analysis., J. Comput. Appl. Math., 2013, 239(1), 72-92.
Google Scholar
|
|
[7]
|
P. Assari, H. Adibi and M. Dehghan, A numerical method for solving linear integral equations of the second kind on the non-rectangular domains based on the meshless method, Appl. Math. Model., 2013, 37(22), 9269-9294. doi: 10.1016/j.apm.2013.04.047
CrossRef Google Scholar
|
|
[8]
|
P. Assari, H. Adibi and M. Dehghan, A meshless discrete Galerkin (MDG) method for the numerical solution of integral equations with logarithmic kernels, J. Comput. Appl. Math., 2014, 267, 160-181. doi: 10.1016/j.cam.2014.01.037
CrossRef Google Scholar
|
|
[9]
|
P. Assari, H. Adibi and M. Dehghan, A meshless method based on the moving least squares (MLS) approximation for the numerical solution of two-dimensional nonlinear integral equations of the second kind on non-rectangular domains, Numer. Algor., 2014, 67(2), 423-455. doi: 10.1007/s11075-013-9800-1
CrossRef Google Scholar
|
|
[10]
|
P. Assari, H. Adibi and M. Dehghan, The numerical solution of weakly singular integral equations based on the meshless product integration (MPI) method with error analysis, Appl. Numer. Math., 2014, 81, 76-93. doi: 10.1016/j.apnum.2014.02.013
CrossRef Google Scholar
|
|
[11]
|
P. Assari and M. Dehghan, A meshless discrete Galerkin method based on the free shape parameter radial basis functions for solving Hammerstein integral equations, Numer. Math. Theor. Meth. Appl., 2018, 11, 541-569.
Google Scholar
|
|
[12]
|
P. Assari and M. Dehghan, The numerical solution of two-dimensional logarithmic integral equations on normal domains using radial basis functions with polynomial precision, Eng. Comput., 2017. DOI: 10.1007/s00366-017-0502-5.
CrossRef Google Scholar
|
|
[13]
|
K. E. Atkinson, The numerical evaluation of fixed points for completely continuous operators, SIAM J. Numer. Anal., 1973, 10, 799-807. doi: 10.1137/0710065
CrossRef Google Scholar
|
|
[14]
|
K. E. Atkinson, The Numerical Solution of Integral Equations of the Second Kind, Cambridge University Press, Cambridge, 1997.
Google Scholar
|
|
[15]
|
K. E. Atkinson and A. Bogomolny, The discrete Galerkin method for integral equations, Math. Comp., 1987, 48, 595-616. doi: 10.1090/S0025-5718-1987-0878693-6
CrossRef Google Scholar
|
|
[16]
|
K. E. Atkinson and J. Flores, The discrete collocation method for nonlinear integral equations, IMA J. Numer. Anal., 1993, 13(2), 195-213.
Google Scholar
|
|
[17]
|
E. Babolian, S. Bazm and P. Lima, Numerical solution of nonlinear two-dimensional integral equations using rationalized Haar functions, Commun. Nonlinear. Sci. Numer. Simulat., 2011, 16(3), 1164-1175. doi: 10.1016/j.cnsns.2010.05.029
CrossRef Google Scholar
|
|
[18]
|
S. Bazm and E. Babolian, Numerical solution of nonlinear two-dimensional Fredholm integral equations of the second kind using gauss product quadrature rules, Commun. Nonlinear. Sci. Numer. Simulat., 2012, 17(3), 1215-1223. doi: 10.1016/j.cnsns.2011.08.017
CrossRef Google Scholar
|
|
[19]
|
M. D. Buhmann, Radial Basis Functions: Theory and Implementations, Cambridge University Press, Cambridge, 2003.
Google Scholar
|
|
[20]
|
V. Carutasu, Numerical solution of two-dimensional nonlinear Fredholm integral equations of the second kind by spline functions, General. Math., 2001, 9, 31-48.
Google Scholar
|
|
[21]
|
W. Chen and W. Lin, Galerkin trigonometric wavelet methods for the natural boundary integral equations, Appl. Math. Comput., 2001, 121(1), 75-92.
Google Scholar
|
|
[22]
|
P. Dasa, G. Nelakantia and G. Longb, Discrete Legendre spectral projection methods for Fredholm-Hammerstein integral equations, J. Comput. Appl. Math., 2015, 278, 293-305. doi: 10.1016/j.cam.2014.10.012
CrossRef Google Scholar
|
|
[23]
|
M. Dehghan and R. Salehi, The numerical solution of the non-linear integro-differential equations based on the meshless method, J. Comput. Appl. Math., 2012, 236(9), 2367-2377. doi: 10.1016/j.cam.2011.11.022
CrossRef Google Scholar
|
|
[24]
|
W. Fang, Y. Wang and Y. Xu, An implementation of fast wavelet Galerkin methods for integral equations of the second kind, J. Sci. Comput., 2004, 20(2), 277-302.
Google Scholar
|
|
[25]
|
R. Farengo, Y.C. Lee and P.N. Guzdar, An electromagnetic integral equation: Application to microtearing modes, Phys. Fluids, 1983, 26(12), 3515-3523. doi: 10.1063/1.864112
CrossRef Google Scholar
|
|
[26]
|
G. E. Fasshauer, Meshfree methods, In: Handbook of Theoretical and Computational Nanotechnology, American Scientific Publishers, 2005.
Google Scholar
|
|
[27]
|
A. Golbabai and S. Seifollahi, Numerical solution of the second kind integral equations using radial basis function networks, Appl. Math. Comput., 2006, 174(2), 877-883.
Google Scholar
|
|
[28]
|
I. G. Graham, Collocation methods for two dimensional weakly singular integral equations, J. Austral. Math. Soc. (Series B), 1993, 22, 456-473.
Google Scholar
|
|
[29]
|
L. Grammonta, P. B. Vasconcelos and M. Ahuesa, A modified iterated projection method adapted to a nonlinear integral equation, Appl. Math. Comput., 2016, 276, 432-441.
Google Scholar
|
|
[30]
|
H. Guoqiang and W. Jiong, Extrapolation of Nystrom solution for two dimensional nonlinear Fredholm integral equations, J. Comput. Appl. Math., 2001, 134(1-2), 259-268. doi: 10.1016/S0377-0427(00)00553-7
CrossRef Google Scholar
|
|
[31]
|
H. Guoqiang and W. Jiong., Richardson extrapolation of iterated discrete Galerkin solution for two-dimensional Fredholm integral equations, J. Comput. Appl. Math., 2002, 139, 49-63. doi: 10.1016/S0377-0427(01)00390-9
CrossRef Google Scholar
|
|
[32]
|
H. Guoqiang, W. Jiong, K. Hayami and X. Yuesheng, Correction method and extrapolation method for singular two-point boundary value problems, J. Comput. Appl. Math., 2000, 126(1-2), 145-157. doi: 10.1016/S0377-0427(99)00349-0
CrossRef Google Scholar
|
|
[33]
|
R. Hanson and J. Phillips, Numerical solution of two-dimensional integral equations using linear elements source, SIAM J. Numer. Anal., 1978, 15, 113-121. doi: 10.1137/0715007
CrossRef Google Scholar
|
|
[34]
|
H. Kaneko and Y. Xu, Gauss-type quadratures for weakly singular integrals and their application to Fredholm integral equations of the second kind, Math. Comp., 1994, 62(206), 739-753. doi: 10.1090/S0025-5718-1994-1218345-X
CrossRef Google Scholar
|
|
[35]
|
H. Kaneko and Y. Xu, Superconvergence of the iterated Galerkin methods for Hammerstein equations, SIAM J. Numer. Anal., 1996, 33(3), 1048-1064.
Google Scholar
|
|
[36]
|
B. Kress, Linear Integral Equations, Springer-Verlag, Berlin, 1989.
Google Scholar
|
|
[37]
|
S. Kumar, A discrete collocation-type method for Hammerstein equations, SIAM J. Numer. Anal., 1998, 25(2), 328-341.
Google Scholar
|
|
[38]
|
S. Kumar and I. H. Sloan, A new collocation type method for Hammerstein integral equations, Math. Comput., 1987, 48(178), 585-593. doi: 10.1090/S0025-5718-1987-0878692-4
CrossRef Google Scholar
|
|
[39]
|
P. Lancaster and K. Salkauskas, Surfaces generated by moving least squares methods, Math. Comput., 1981, 37(155), 141-158. doi: 10.1090/S0025-5718-1981-0616367-1
CrossRef Google Scholar
|
|
[40]
|
X. Li, Meshless Galerkin algorithms for boundary integral equations with moving least square approximations, Appl. Numer. Math., 2011, 61(12), 1237-1256. doi: 10.1016/j.apnum.2011.08.003
CrossRef Google Scholar
|
|
[41]
|
X. Li and J. Zhu, A Galerkin boundary node method and its convergence analysis, J. Comput. Appl. Math., 2009, 230(1), 314-328.
Google Scholar
|
|
[42]
|
X. Li and Q. Wang, Analysis of the inherent instability of the interpolating moving least squares method when using improper polynomial bases, Eng. Anal. Bound. Elem., 20169, 73, 21-34.
Google Scholar
|
|
[43]
|
X. Li, H. Chen and Y. Wang, Error analysis in Sobolev spaces for the improved moving least-square approximation and the improved element-free Galerkin method, Appl. Math. Comput., 2015, 262, 56-78.
Google Scholar
|
|
[44]
|
A. V. Manzhirov, On a method of solving two-dimensional integral equations of axisymmetric contact problems for bodies with complex rheology, J. Appl. Math. Mech., 1985, 49(6), 777-782. doi: 10.1016/0021-8928(85)90016-4
CrossRef Google Scholar
|
|
[45]
|
D. Mirzaei and M. Dehghan, A meshless based method for solution of integral equations, Appl. Numer. Math., 2010, 60(3), 245-262. doi: 10.1016/j.apnum.2009.12.003
CrossRef Google Scholar
|
|
[46]
|
Y. Ordokhani, Solution of Fredholm-Hammerstein integral equations with walsh-hybrid functions, Int. Math. Forum., 2009, 4, 969-976.
Google Scholar
|
|
[47]
|
K. Parand and J. A. Rad, Numerical solution of nonlinear Volterra-Fredholm-Hammerstein integral equations via collocation method based on radial basis functions, Appl. Math. Comput., 2012, 218(9), 5292-5309.
Google Scholar
|
|
[48]
|
A. Pedas and G. Vainikko, Product integration for weakly singular integral equations in $m$ dimensional space, In: B.Bertram, C.Constanda, A.Struthers (Ed.), Integral Methods in Science and Engineering, 280-285, Chapman and Hall/CRC, 2000.
Google Scholar
|
|
[49]
|
A. Quarteroni, R. Sacco and F. Saleri, Numerical Analysis for Electromagnetic Integral Equations, Artech House, Boston, 2008.
Google Scholar
|
|
[50]
|
A. Tari, M. Y. Rahimi, S. Shahmorad and F. Talati, Solving a class of two-dimensional linear and nonlinear Volterra integral equations by the differential transform method, J. Comput. Appl. Math., 2009, 228(1), 70-76.
Google Scholar
|
|
[51]
|
A. M. Wazwaz, Linear and Nonlinear Integral equations: Methods and Applications, Higher Education Press and Springer Verlag, Heidelberg, 2011.
Google Scholar
|
|
[52]
|
H. Wendland, Scattered Data Approximation, Cambridge University Press, New York, 2005.
Google Scholar
|




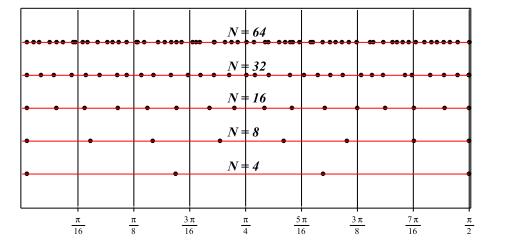

 DownLoad:
DownLoad: