| Citation: |
Jingliang Lv, Xiaoling Zou, Yujie Li. DYNAMICAL PROPERTIES OF A STOCHASTIC PREDATOR-PREY MODEL WITH FUNCTIONAL RESPONSE[J]. Journal of Applied Analysis & Computation, 2020, 10(4): 1242-1255. doi: 10.11948/20190104
|
DYNAMICAL PROPERTIES OF A STOCHASTIC PREDATOR-PREY MODEL WITH FUNCTIONAL RESPONSE
-
Abstract
A stochastic prey-predator model with functional response is investigated in this paper. A complete threshold analysis of coexistence and extinction is obtained. Moreover, we point out that the stochastic predator-prey model undergoes a stochastic Hopf bifurcation from the viewpoint of numerical simulations. Some numerical simulations are carried out to support our results. -
-
References
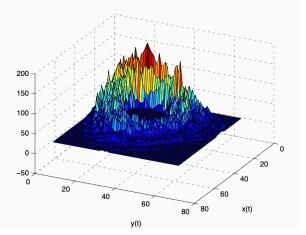
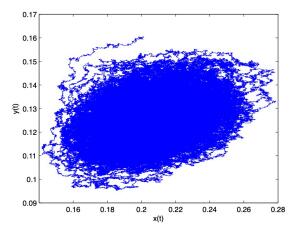
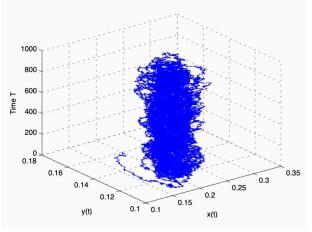
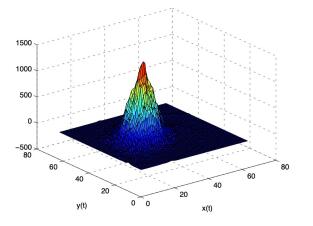
[1] J. R. Beddington, Mutual interference between parasites or predators and its effect on searching efficiency, J. Anim. Ecol., 1975, 44, 331-340. doi: 10.2307/3866 [2] Y. Chen, Z. Liu and M. Haque, Analysis of a Leslie-Gower-type prey-predator model with periodic impulsive perturbations, Commun. Nonlinear Sci., 2009, 14, 3412-3423. doi: 10.1016/j.cnsns.2008.12.019 [3] S. Chen, J. Wei and J. Yu, Stationary patterns of a diffusive predator-prey model with Crowley-Martin functional response, Nonliear Anal.-Real., 2018, 39, 33-57. doi: 10.1016/j.nonrwa.2017.05.005 [4] C. Chiarella, X. He, D. Wang and M. Zheng, The stochastic bifurcation behaviour of speculative financial markets, Physica A., 2008, 387, 3837-3846. doi: 10.1016/j.physa.2008.01.078 [5] P. H. Crowley and E. K. Martin, Functional responses and interference within and between year classes of a dragonfly population, J. N. Am. Benthol. Soc., 1989, 8, 211-221. doi: 10.2307/1467324 [6] D. L. DeAngelis, R. A. Goldsten and R. V. O'Neill, A model for trophic interaction, Ecology., 1975, 56, 881-892. doi: 10.2307/1936298 [7] T. S. Doan, M. Engel, J. S. W. Lamb and M. Rasmussen, Hopf bifurcation with additive noise, Nonlinearity., 2018, 31(10), 4567-4601. doi: 10.1088/1361-6544/aad208 [8] N. Du, D. H. Nguyen and G. Yin, Conditions for permanence and ergodicity of certain stochastic predator-prey models, J. Appl. Probab., 2016, 53, 187- šC202. doi: 10.1017/jpr.2015.18 [9] T. C. Gard, Persistence in stochastic food web models, B. Math. Biol., 1984, 46, 357-370. doi: 10.1016/S0092-8240(84)80044-0 [10] T. C. Gard, Stability for multispecies population models in random environments, Nonlinear Anal., 1986, 10, 1411-1419. doi: 10.1016/0362-546X(86)90111-2 [11] M. P. Hassell and G. C. Varley, New inductive population model for intersect parasites and its bearing on biological control, Nature. 1969, 223, 1133-1137. doi: 10.1038/2231133a0 [12] A. Hening and D. H. Nguyen, Coexistence and extinction for stochastic Kolmogorov systems, Ann. Appl. Probab., 2018, 28, 1893-1942. doi: 10.1214/17-AAP1347 [13] A. Hening and D. H. Nguyen, Persistence in stochastic Lotka-Volterra food chains with intraspecific competition, Bull. Math. Biol., 2018, 80, 2527-2560. doi: 10.1007/s11538-018-0468-5 [14] Z. Huang, Q. Yang and J. Cao, Stochastic stability and bifurcation for the chronic state in Marchuk's model with noise, Appl. Math. Model., 2011, 35, 5842-5855. doi: 10.1016/j.apm.2011.05.027 [15] D. Huang, H. Wang, J. Feng and Z. Zhu, Hopf bifurcation of the stochastic model on HAB nonlinear stochastic dynamics, Chaos Solit. Fract., 2006, 27, 1072-1079. doi: 10.1016/j.chaos.2005.04.086 [16] C. Ji, D. Jiang and N. Shi, Analysis of a predator-prey model with modified Leslie-Gower and Holling-type II schemes with stochastic perturbation, J. Math. Anal. Appl., 2009, 359, 482-498. doi: 10.1016/j.jmaa.2009.05.039 [17] W. Li, W. Xu, J. Zhao and Y. Jin, Stochastic stability and bifurcation in a macroeconomic model, Chaos Solit. Fract., 2007, 31, 702-711. doi: 10.1016/j.chaos.2005.10.024 [18] X. Liu, S. Zhong, B. Tian and F. Zheng, Asymptotic of a stochastic predator-prey model with Crowley-Martin functional response, J. Appl. Math. Comput., 2013, 43, 479-490. doi: 10.1007/s12190-013-0674-0 [19] J. Lv, H. Liu and X. Zou, Stationary distribution and persistence of a stochastic predator-prey model with a functional response, J. Appl. Anal. Comput., 2019, 9(1), 1-11. doi: 10.11948/2019.1 [20] A. P. Maiti, B. Dubey and J. Tushar, A delayed prey-predator model with Crowley-Martin-type functional response including prey refuge, Math. Method Appl. Sci., 2017, 40, 5792-5809. doi: 10.1002/mma.4429 [21] R. M. May, Stability and Complexity in Model Ecosystems, Princeton University Press, Princeton, 1973. [22] G. Pang, F. Wang and L. Chen, Extinction and permanence in delayed stage-structure predator-prey system with impulsive effects, Chaos Soliton. Frac., 2009, 39, 2216-2224. doi: 10.1016/j.chaos.2007.06.071 [23] K. R. Schenk-Hopp$\acute{e}$, Stochastic hopf bifurcation: an example, Int. J. Non-Lin Mech., 1996, 31, 685-692. doi: 10.1016/0020-7462(96)00030-3 [24] H. Shi and S. Ruan, Spatial, temporal and spatiotemporal patterns of diffusive predator-prey models with mutual interference, IMA J. Appl. Math., 2015, 80, 1534-1568. doi: 10.1093/imamat/hxv006 [25] X. Shi, X. Zho and X. Song, Analysis of a stage-structured predator-prey model with Crowley-Martin function, J. Appl. Math. Comput., 2011, 36, 459-472. doi: 10.1007/s12190-010-0413-8 [26] J. P. Tripathi, S. Tyagi and S. Abbas, Global analysis of a delayed density dependent predator-prey model with Crowley-Martin functional response, Commun. Nonlinear Sci., 2016, 30, 45-69. doi: 10.1016/j.cnsns.2015.06.008 [27] C. Wang, Z. Xiong, R. He and H. Yin, Dynamical behaviors of stochastic delayed one-predator and two-competing-prey systems with Holling type IV and Crowley-Martin type functinal responses, Discrete Dyn. Nat. Soc., 2016, 7676101, 1-16. [28] Y. Zhang, S. Gao, K. Fan and Y. Dai, On the dynamics of a stochastic ratio-dependent predator-prey model with a specific functional reponse, J. Comput. Math. Appl., 2015, 48, 441-460. doi: 10.1007/s12190-014-0812-3 [29] Z. Sun, J. Lv and X. Zou, Dynamical analysis on two stochastic single-species models, Appl. Math. Lett., 2020. DOI: 10.1016/j.aml.2019.07.013. [30] X. Zou, Y. Zheng, L. Zhang and J. Lv, Survivability and stochastic bifurcations for a stochastic Holling type II predator-prey model, Commun. Nonlinear Sci., 2020. DOI: 10.1016/j.cnsns.2019.105136. [31] X. Zou, J. Lv and Y. Wu, A note on a stochastic Holling-II predator-prey model with a prey refuge, J. Franklin Inst., 2020, 357(7), 4486-4502. doi: 10.1016/j.jfranklin.2020.03.013 [32] J. Zhou, Qualitative analysis of a modified Leslie-Gower predator-prey model with Crowley-Martin functional responses, Commun. Pur. Appl. Anal., 2015, 14, 1127-1145. doi: 10.3934/cpaa.2015.14.1127 [33] X. Zhou and J. Cui, Global stability of the viral dynamics with crowley-martin functional response, Bull. Korean Math. Soc., 2011, 48, 555-574. doi: 10.4134/BKMS.2011.48.3.555 [34] X. Zou, K. Wang and D. Fan, Stochastic Poincare-Bendixson theorem and its application on stochastic hopf bifurcation, Int. J. Bifurcat. Chaos., 2013, 23(4), 1-14. doi: 10.1142/S0218127413500703 -
-
Figures(21) / Tables(2)
Export File
Citation
Jingliang Lv, Xiaoling Zou, Yujie Li. DYNAMICAL PROPERTIES OF A STOCHASTIC PREDATOR-PREY MODEL WITH FUNCTIONAL RESPONSE[J]. Journal of Applied Analysis & Computation, 2020, 10(4): 1242-1255. doi: 10.11948/20190104
Format
Content
DownLoad:
-
Figure 1. both
$ x $ and$ y $ go extinct -
Figure 2.
$ x $ is persistent and$ y $ goes extinct -
Figure 3. both
$ x $ and$ y $ are persistent -
Figure 4. both
$ x $ and$ y $ go extinct -
Figure 5.
$ x $ is persistent and$ y $ goes extinct -
Figure 6. both
$ x $ and$ y $ are persistent -
Figure 7.
$ x $ goes extinct and$ y $ is persistent -
Figure 8.
$ x $ goes extinct and$ y $ is persistent -
Figure 9. both
$ x $ and$ y $ are persistent - Figure 10. Periodic solution for the system (3.1)
- Figure 11. A stable limit cycle for the system (3.3) in phase space.
- Figure 12. A stable limit cycle for the system (3.3) in three-dimensional space introducing time axis.
- Figure 13. A stable positive equilibrium point for the system (3.4).
- Figure 14. A stable positive equilibrium point for the system (3.4) in phase space.
- Figure 15. A stable positive equilibrium point for the system (3.4) in three-dimensional space introducing time axis.
- Figure 16. A stochastic limit cycle for the system (3.1) in phase space.
- Figure 17. A stochastic limit cycle for the system (3.1) in three-dimensional space introducing time axis.
- Figure 18. A crater-like stationary distribution for the system (3.1) in three-dimensional space.
- Figure 19. A stochastic solution process for the system (3.2) in phase space.
- Figure 20. A stochastic solution process for the system (3.2) in three-dimensional space introducing time axis.
- Figure 21. A peak-like stationary distribution for the system (3.2) in three-dimensional space.