| Citation: | E. M. Elsayed, Faris Alzahrani, Ibrahim Abbas, N. H. Alotaibi. DYNAMICAL BEHAVIOR AND SOLUTION OF NONLINEAR DIFFERENCE EQUATION VIA FIBONACCI SEQUENCE[J]. Journal of Applied Analysis & Computation, 2020, 10(1): 282-296. doi: 10.11948/20190143 |
DYNAMICAL BEHAVIOR AND SOLUTION OF NONLINEAR DIFFERENCE EQUATION VIA FIBONACCI SEQUENCE
-
Abstract
In this paper, we study the behavior of the difference equation $x_{n+1}=ax_{n}+\dfrac{bx_{n}x_{n-1}}{cx_{n-1}+dx_{n-2}},~n=0,1,\ldots,$ where the initial conditions $x_{-2},\ x_{-1},\ x_{0}$ are arbitrary positive real numbers and $a,b,c,d$ are positive constants. Also, we give the solution of some special cases of this equation.-
Keywords:
- Stability /
- boundedness /
- solution of difference equations
-

-
References
[1] M. A. E. Abdelrahman, G. E Chatzarakis, T. Li and O. Moaaz, On the difference equation $ x_{n+1}=ax_{n-l}+bx_{n-k}+f(x_{n-l}, x_{n-k})$, Advances in Difference Equations, 2018, 2018(1), 431. doi: 10.1186/s13662-018-1880-8 CrossRef $ x_{n+1}=ax_{n-l}+bx_{n-k}+f(x_{n-l}, x_{n-k})$" target="_blank">Google Scholar
[2] M. A. E. Abdelrahman and O. Moaaz, On the new class of the nonlinear rational difference equations, Electronic Journal of Mathematical Analysis and Applications, 2018, 6(1), 117-125. [3] R. Abo-Zeid, Global behavior of two third order rational difference equations with quadratic terms, Mathematica Slovaca, 2019, 69(1), 147-158. doi: 10.1515/ms-2017-0210 [4] R. P. Agarwal and E. M. Elsayed, Periodicity and stability of solutions of higher order rational difference equation, Advanced Studies in Contemporary Mathematics, 2008, 17(2), 181-201. [5] M. B. Almatrafi, E. M. Elsayed and F. Alzahrani, Investigating some properties of a fourth order difference equation, Journal of Computational Analysis and Applications, 2020, 28(2), 243-253. [6] M. Aloqeili, Dynamics of a rational difference equation, Applied Mathematics and Computation, 2006, 176(2), 768-774. doi: 10.1016/j.amc.2005.10.024 [7] M. Aloqeili, Dynamics of a kth order rational difference equation, Applied Mathematics and Computation, 2006, 181, 1328-1335. doi: 10.1016/j.amc.2006.03.001 [8] A. M. Alotaibi, M. S. M. Noorani and M. A. El-Moneam, On the periodicity of the solution of a rational difference equation, Communications Faculty of Sciences University of Ankara Series A1-Mathematics and Statistics, 2019, 68(2), 1427-1434. [9] A. M. Alotaibi, M. Noorani and M. A. El-Moneam, Periodicity of the solution of a higher order difference equation, AIP Conference Proceedings, 2018, 2013(1), 020018. [10] M. Atalay, C. Cinar and I. Yalcinkaya, On the positive solutions of systems of difference equations, International Journal of Pure and Applied Mathematics, 2005, 24(4), 443-447. [11] F. Belhannache, Asymptotic stability of a higher order rational difference equation, Electronic Journal of Mathematical Analysis and Applications, 2019, 7(2), 1-8. [12] C. Cinar, On the positive solutions of the difference equation $x_{n+1}=\frac{x_{n-1}}{1+ax_{n}x_{n-1}}, \ $Applied Mathematics and Computation, 2004, 158(3), 809-812. doi: 10.1016/j.amc.2003.08.140 CrossRef $x_{n+1}=\frac{x_{n-1}}{1+ax_{n}x_{n-1}}\ $" target="_blank">Google Scholar
[13] C. Cinar, On the positive solutions of the difference equation $x_{n+1}=\frac{x_{n-1}}{-1+ax_{n}x_{n-1}}, \ $Applied Mathematics and Computation, 2004, 158(3), 793-797. doi: 10.1016/j.amc.2003.08.139 CrossRef $x_{n+1}=\frac{x_{n-1}}{-1+ax_{n}x_{n-1}}\ $" target="_blank">Google Scholar
[14] C. Cinar, On the positive solutions of the difference equation $x_{n+1}=\frac{ax_{n-1}}{1+bx_{n}x_{n-1}}, $ Applied Mathematics and Computation, 2004, 156, 587-590. doi: 10.1016/j.amc.2003.08.010 CrossRef $x_{n+1}=\frac{ax_{n-1}}{1+bx_{n}x_{n-1}}$" target="_blank">Google Scholar
[15] Q. Din and W. Ishaque, Bifurcation analysis and chaos control in discrete-time eco-epidemiological models of pelicans at risk in the Salton Sea, International Journal of Dynamics and Control, 2019, 1-17. DOI: 10.1007/s40435-019-00508-x. [16] Q. Din, A. A. Elsadany and S. Ibrahim, Bifurcation analysis and chaos control in a second-order rational difference equation, International Journal of Nonlinear Sciences and Numerical Simulation, 2018, 19(1), 53-68. doi: 10.1515/ijnsns-2017-0077 [17] E. M. Elabbasy, H. El-Metwally and E. M. Elsayed, On the difference equation $\ x_{n+1}=ax_{n}-\frac{bx_{n}}{cx_{n}-dx_{n-1}}, $ Advances in Difference Equations, 2006, Volume 2006, Article ID 82579, 1-10. [18] E. M. Elabbasy, H. El-Metwally and E. M. Elsayed, On the difference equations $x_{n+1}=\frac{\alpha x_{n-k}}{\beta +\gamma \prod_{i=0}^{k}x_{n-i}}, $ Journal of Concrete and Applicable Mathematics, 2007, 5(2), 101-113. [19] M. M. El-Dessoky, E. M. Elabbasy and A. Asiri, Dynamics and solutions of a fifth-order nonlinear difference equation, Discrete Dynamics in Nature and Society, 2018, Volume 2018, Article ID 9129354, 21 pages. [20] H. El-Metwally and M. M. El-Afifi, On the behavior of some extension forms of some population models, Chaos, Solitons and Fractals, 2008, 36, 104-114. doi: 10.1016/j.chaos.2006.06.043 [21] M. A. El-Moneam, A. Q. Khan, E. S. Aly and M. A. Aiyashi, Behavior of a system of higher-order difference equations, Journal of Computational Analysis and Applications, 2020, 28(5), 808-813. [22] E. M. Elsayed and M. Alzubaidi, The form of the solutions of system of rational difference equation, Journal of Mathematical Sciences and Modelling, 2018, 1(3), 181-191. doi: 10.33187/jmsm.427368 [23] M. Folly-Gbetoula and D. Nyirenda, On some rational difference equations of order eight, International Journal of Contemporary Mathematical Sciences, 2018, 13(6), 239-254. [24] M. Gümüş, Global dynamics of a third-order rational difference equation, Karaelmas Science and Engineering Journal, 2018, 8(2), 585-589. [25] O. Guner, Exact travelling wave solutions to the space-time fractional Calogero-Degasperis equation using different methods, Journal of Applied Analysis and Computation, 2019, 9(2), 428-439. [26] A. E. Hamza and A. Morsy, On the recursive sequence $ x_{n+1}=\frac{A\prod_{i=l}^{k}x_{n-2i-1}}{B+C\prod_{i=l}^{k-1}x_{n-2i}}, $ Computers and Mathematics with Applications, 2008, 56(7), 1726-1731. doi: 10.1016/j.camwa.2008.04.014 CrossRef $ x_{n+1}=\frac{A\prod_{i=l}^{k}x_{n-2i-1}}{B+C\prod_{i=l}^{k-1}x_{n-2i}}$" target="_blank">Google Scholar
[27] T. F. Ibrahim, On the third order rational difference equation $x_{n+1}=\frac{x_{n}x_{n-2}}{x_{n-1}(a+bx_{n}x_{n-2})}, $ International Journal of Contemporary Mathematical Sciences, 2009, 4(27), 1321-1334. $x_{n+1}=\frac{x_{n}x_{n-2}}{x_{n-1}(a+bx_{n}x_{n-2})}$" target="_blank">Google Scholar
[28] T. F. Ibrahim, Bifurcation and periodically semicycles for fractional difference equation of fifth order, Journal of Nonlinear Sciences and Applications, 2018, 11(3), 375-382. doi: 10.22436/jnsa.011.03.06 [29] T. F. Ibrahim, Generalized partial ToDD's difference equation in n-dimensional space, Journal of Computational Analysis and Applications, 2019, 26(5), 910-926. [30] S. Kang, H. Chen, L. Li, Y. Cui and S. Ma, Existence of three positive solutions for a class of Riemann-Liouville fractional q-difference equation, Journal of Applied Analysis and Computation, 2019, 9(2), 590-600. [31] R. Karatas, C. Cinar and D. Simsek, On positive solutions of the difference equation $x_{n+1}=\frac{x_{n-5}}{1+x_{n-2}x_{n-5}}, $ International Journal of Contemporary Mathematical Sciences, 2006, 1(10), 495-500. $x_{n+1}=\frac{x_{n-5}}{1+x_{n-2}x_{n-5}}$" target="_blank">Google Scholar
[32] A. Khaliq, On the solution and periodic nature of higher-order difference equation, Mathematical Sciences Letters, 2017, 6(2), 177-1867. doi: 10.18576/msl/060210 [33] A. Kurbanli, A study on Heron triangles and difference equations, AIP Conference Proceedings 2018, 1997, 020007. https://doi.org/10.1063/1.5049001. doi: 10.1063/1.5049001 [34] V. L. Kocic and G. Ladas, Global Behavior of Nonlinear Difference Equations of Higher Order with Applications, Kluwer Academic Publishers, Dordrecht, 1993. [35] M. R. S. Kulenovic and G. Ladas, Dynamics of Second Order Rational Difference Equations with Open Problems and Conjectures, Chapman & Hall / CRC Press, 2001. [36] O. Ocalan and O. Dumanon, Solutions of the recursive equations $x_{n+1}=x_{n-1}^{p}/x_{n}^{p}$ $(p>0), $ via Fibonacci type sequences, Electronic Journal of Mathematical Analysis and Applications, 2019, 7(1), 102-115. [37] S. Sadiq and M. Kalim, Global attractivity of a rational difference equation of order twenty, International Journal of Advanced and Applied Sciences, 2018, 5(2), 1-7. doi: 10.21833/ijaas.2018.02.001 [38] M. Saleh and S. Abu-Baha, Dynamics of a higher order rational difference equation, Applied Mathematics and Computation, 2006, 181, 84-102. doi: 10.1016/j.amc.2006.01.012 [39] M. Saleh and M. Aloqeili, On the difference equation $ x_{n+1}=A+\frac{x_{n}}{x_{n-k}}$, Applied Mathematics and Computation, 2005, 171, 862-869. doi: 10.1016/j.amc.2005.01.094 CrossRef $ x_{n+1}=A+\frac{x_{n}}{x_{n-k}}$" target="_blank">Google Scholar
[40] D. Simsek, C. Cinar and I. Yalcinkaya, On the recursive sequence $x_{n+1}=\frac{x_{n-3}}{1+x_{n-1}}, $ International Journal of Contemporary Mathematical Sciences, 2006, 1(10), 475-480. $x_{n+1}=\frac{x_{n-3}}{1+x_{n-1}}$" target="_blank">Google Scholar
[41] C. Wang, S. Wang and X. Yan, Global asymptotic stability of 3-species mutualism models with diffusion and delay effects, Discrete Dynamics in Natural and Science, 2009, Volume 2009, Article ID 317298, 20 pages. [42] C. Wang, F. Gong, S. Wang, L. LI and Q. Shi, Asymptotic behavior of equilibrium point for a class of nonlinear difference equation, Advances in Difference Equations, 2009, Volume 2009, Article ID 214309, 8 pages. [43] I. Yalcinkaya, C. Çinar and M. Atalay, On the solutions of systems of difference equations, Advances in Difference Equations, 2008, Vol. 2008, Article ID 143943, 9 pages. [44] I. Yalçınkaya, On the global asymptotic behavior of a system of two nonlinear difference equations, ARS Combinatoria, 2010, 95, 151-159. [45] I. Yalçınkaya, On the global asymptotic stability of a second-order system of difference equations, Discrete Dynamics in Nature and Society, 2008, Vol. 2008, Article ID 860152, 12 pages. DOI: 10.1155/2008/860152. [46] I. Yalçınkaya, On the difference equation $ x_{n+1}=\alpha +\frac{x_{n-m}}{x_{n}^{k}}$, Discrete Dynamics in Nature and Society, 2008, Vol. 2008, Article ID 805460, 8 pages. DOI: 10.1155/2008/805460. [47] E. M. E. Zayed and M. A. El-Moneam, On the rational recursive sequence $x_{n+1}=\frac{\alpha +\beta x_{n}+\gamma x_{n-1}}{ A+Bx_{n}+Cx_{n-1}}, $ Communications on Applied Nonlinear Analysis, 2005, 12(4), 15-28. [48] E. M. E. Zayed and M. A. El-Moneam, On the rational recursive sequence $ x_{n+1}=ax_{n}-\frac{bx_{n}}{cx_{n}-dx_{n-k}}$, Communications on Applied Nonlinear Analysis, 2008, 15, 47-57. $ x_{n+1}=ax_{n}-\frac{bx_{n}}{cx_{n}-dx_{n-k}}$" target="_blank">Google Scholar
[49] E. M. E. Zayed and M. A. El-Moneam, On the rational recursive sequence $x_{n+1}=\frac{\alpha x_{n}+\beta x_{n-1}+\gamma x_{n-2}+\delta x_{n-3}}{Ax_{n}+Bx_{n-1}+Cx_{n-2}+Dx_{n-3}}$; Communications on Applied Nonlinear Analysis, 2005, 12, 15-28. -
-
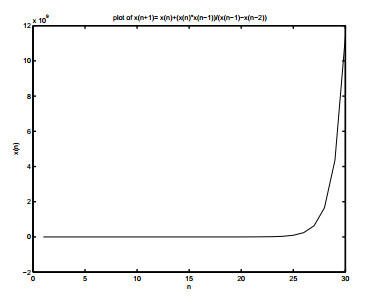
- Figure 1.
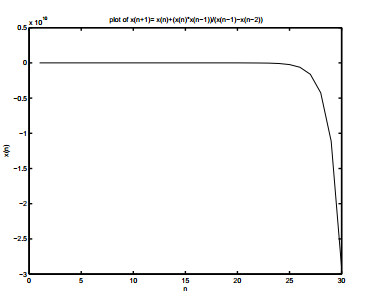
- Figure 2.
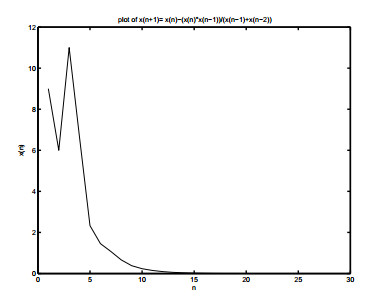
- Figure 3.
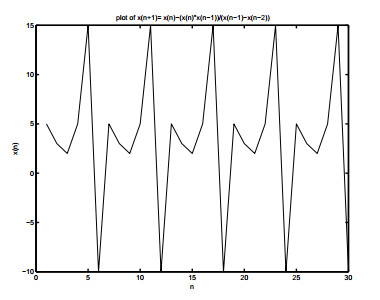
- Figure 4.
- Figure 5.




 DownLoad:
DownLoad: