| Citation: | Chanchal Garodia, Izhar Uddin. A NEW ITERATIVE METHOD FOR SOLVING SPLIT FEASIBILITY PROBLEM[J]. Journal of Applied Analysis & Computation, 2020, 10(3): 986-1004. doi: 10.11948/20190179 |
A NEW ITERATIVE METHOD FOR SOLVING SPLIT FEASIBILITY PROBLEM
-
Abstract
In this paper, we construct a new iterative algorithm and show that the newly introduced iterative algorithm converges faster than a number of existing iterative algorithms for contractive-like mappings. We present a numerical example followed by graphs to validate our claim. We prove strong and weak convergence results for approximating fixed points of generalized $\alpha$-nonexpansive mappings. Again we reconfirm our results by an example and table. Further, we utilize our proposed algorithm to solve split feasibility problem. -

-
References
[1] M. Abbas and T. Nazir, A new faster iteration process applied to constrained minimization and feasibility problems, Matematicki Vesnik, 2014, 66(2), 223-234. [2] R. P. Agarwal, D. Ó Regan and D. R. Sahu, Iterative construction of fixed points of nearly asymptotically nonexpansive mappings, Journal of Nonlinear and Convex Analysis, 2007, 8(1), 61-79. [3] K. Aoyama and F. Kohsaka, Fixed point theorem for $\alpha$-nonexpansive mappings in Banach spaces, Nonlinear Anal., 2011, 74, 4387-4391. doi: 10.1016/j.na.2011.03.057 [4] S. Banach, Sur les operations dans les ensembles abstraits et leurs applications, Fundam. Math., 1922, 3, 133-181. [5] V. Berinde, On the convergence of the Ishikawa iteration in the class of quasi contractive operators, Acta Math. Univ. Comen., 2004, 73, 119-126. [6] V. Berinde, Picard iteration converges faster than Mann iteration for a class of quasicontractive operators, Fixed Point Theory and Applications, 2004, 2, 97-105. [7] F. E. Browder, Nonexpansive nonlinear operators in a Banach space, Proc. Nat. Acad. Sci. U.S.A., 1965, 54, 1041-1044. doi: 10.1073/pnas.54.4.1041 [8] C. Byrne, Iterative oblique projection onto convex sets and the split feasibility problem, Inverse Probl., 2002, 18(2), 441-453. [9] Y. Censor and T. Elfving, A multiprojection algorithm using Bregman projections in a product space, Numer. Algorithms, 1994, 8(24), 221-239. [10] M. Feng, L. Shi and R. Chen, A new three-step iterative algorithm for solving the split feasibility problem, U. P. B. Sci. Bull., Series A, 2019, 81(1), 93-102. [11] D. Göhde, Zum Prinzip der kontraktiven abbildung. Math, Nachr., 1965, 30, 251-258. doi: 10.1002/mana.19650300312 [12] N. Hussain, K. Ullah and M. Arshad, Fixed point approximation for Suzuki generalized nonexpansive mappings via new iteration process, Journal of Nonlinear and Convex Analysis, 2018, 19(8), 1383-1393. [13] C. O. Imoru and M. O. Olantiwo, On the stability of the Picard and Mann iteration processes, Carpath. J. Math., 2003, 19, 155-160. [14] S. Ishikawa, Fixed points by a new iteration method, Proc. Amer. Math. Soc., 1974, 44, 147-150. doi: 10.1090/S0002-9939-1974-0336469-5 [15] W. A. Kirk, A fixed point theorem for mappings which do not increase distances, Amer. Math. Monthly, 1965, 72, 1004-1006. doi: 10.2307/2313345 [16] W. R. Mann, Mean value methods in iteration, Proc. Am. Math. Soc., 1953, 4, 506-510. doi: 10.1090/S0002-9939-1953-0054846-3 [17] M. A. Noor, New approximation schemes for general variational inequalities, Journal of Mathematical Analysis and Applications, 2000, 251(1), 217-229. [18] R. Pant and R. Shukla, Approximating Fixed Points of Generalized $\alpha$-Nonexpansive Mappings in Banach Spaces, Numerical Functional Analysis and Optimization, 2017, 38(2), 248-266. doi: 10.1080/01630563.2016.1276075 CrossRef $\alpha$-Nonexpansive Mappings in Banach Spaces" target="_blank">Google Scholar
[19] H. Piri, B. Daraby, S. Rahrovi and M. Ghasemi, Approximating fixed points of generalized $\alpha$-nonexpansive mappings in Banach spaces by new faster iteration process, Numerical Algorithm, 2018. [20] J. Schu, Weak and strong convergence to fixed points of asymptotically nonexpansive mappings, Bulletin of the Australian Mathematical Society, 1991, 43, 153-159. doi: 10.1017/S0004972700028884 [21] H. F. Senter and W. G. Dotson, Approximating fixed points of nonexpansive mappings, Proceedings of the American Mathematical Society, 1974, 44(2), 375-380. doi: 10.1090/S0002-9939-1974-0346608-8 [22] T. Suzuki, Fixed point theorems and convergence theorems for some generalized non-expansive mapping, J. Math. Anal. Appl., 2008, 340, 1088-1095. doi: 10.1016/j.jmaa.2007.09.023 [23] K. Tan and H. Xu, Approximating fixed points of nonexpansive mappings by the Ishikawa iteration process, Journal of Mathematical Analysis and Applications, 1993, 178, 301-308. doi: 10.1006/jmaa.1993.1309 [24] B. S. Thakur, D. Thakur and M. Postolache, A New iteration scheme for approximating fixed points of nonexpansive mappings, Filomat, 2016, 30(10), 2711-2720. doi: 10.2298/FIL1610711T [25] D. Thakur, B. S. Thakur and M. Postolache, A new iterative scheme for numerical reckoning fixed points of Suzuki's generalized nonexpansive mappings, Applied Mathematics and Computation, 2016, 275, 147-155. doi: 10.1016/j.amc.2015.11.065 [26] K. Ullah and M. Arshad, New iteration process and numerical reckoning fixed points in Banach spaces, U. P. B. Sci. Bull., Series A, 2017, 79(4), 113-122. [27] K. Ullah and M. Arshad, Numerical Reckoning Fixed Points for Suzuki's Generalized Nonexpansive Mappings via New Iteration Process, Filomat, 2018, 32(1), 187-196. doi: 10.2298/FIL1801187U [28] K. Ullah and M. Arshad, New three step iteration process and fixed point approximation in Banach spaces, Journal of Linear and Topological Algebra, 2018, 7(2), 87-100. [29] H. Xu, A variable Krasnosel'skii-Mann algorithm and the multiple-set split feasibility problem, Inverse Probl., 2006, 22(6), 2021-2034. doi: 10.1088/0266-5611/22/6/007 [30] H. Xu, Iterative methods for the split feasibility problem in infinite-dimensional Hilbert spaces, Inverse Probl., 26, 105018 (2010), 17pp. [31] T. Zamfirescu, Fix point theorems in metric spaces, Arch. Math., 1972, 23, 292-298. doi: 10.1007/BF01304884 -
-
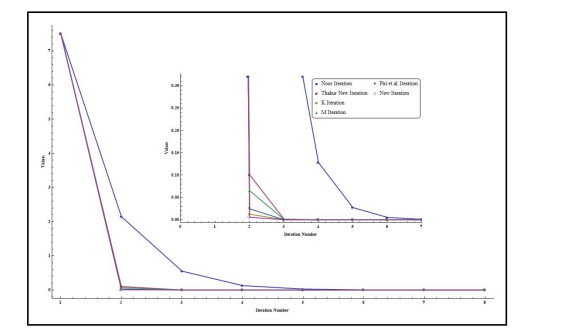
- Figure 1. Graph corresponding to Table 1.
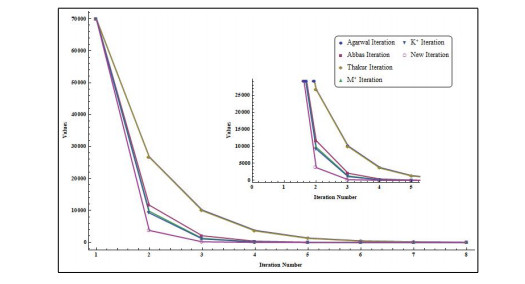
- Figure 2. Graph corresponding to Table 2.
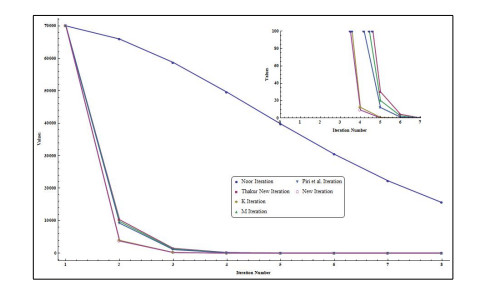
- Figure 3. Graph corresponding to Table 3.
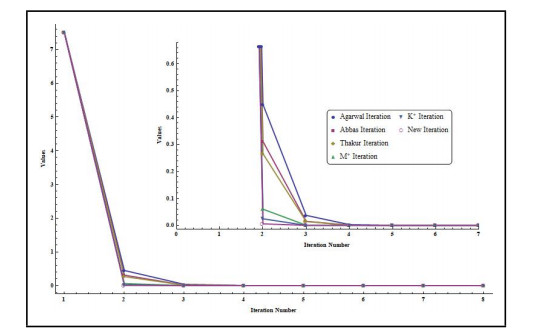
- Figure 4. Graph corresponding to Table 4.




 DownLoad:
DownLoad: