QUALITATIVE ANALYSIS OF A FOURTH ORDER DIFFERENCE EQUATION

H. S. Alayachi; M. S. M. Noorani; E. M. Elsayed

doi:10.11948/20190196

2020 Volume 10 Issue 4

Article Contents

Article navigation > Journal of Applied Analysis & Computation > 2020 > 10(4): 1343-1354

Next Article Previous Article

H. S. Alayachi, M. S. M. Noorani, E. M. Elsayed. QUALITATIVE ANALYSIS OF A FOURTH ORDER DIFFERENCE EQUATION[J]. Journal of Applied Analysis & Computation, 2020, 10(4): 1343-1354. doi: 10.11948/20190196

Citation:

H. S. Alayachi, M. S. M. Noorani, E. M. Elsayed. QUALITATIVE ANALYSIS OF A FOURTH ORDER DIFFERENCE EQUATION[J]. Journal of Applied Analysis & Computation, 2020, 10(4): 1343-1354. doi: 10.11948/20190196

QUALITATIVE ANALYSIS OF A FOURTH ORDER DIFFERENCE EQUATION

1.
School of Mathematical Sciences, Faculty of Science and Technology, Universiti Kebangsaan Malaysia, Bangi, Selangor, Malaysia
2.
Mathematics Department, Faculty of Science, King Abdulaziz University, P. O. Box 80203, Jeddah 21589, Saudi Arabia
3.
Department of Mathematics, Faculty of Science, Mansoura University, Mansoura 35516, Egypt

Corresponding author: HSSHAREEF@taibahu.edu.sa (H. S. Alayachi)

Abstract

Abstract

In this paper, we will investigate some qualitative behavior of solutions of the following fourth order difference equation $ x_{n+1} = ax_{n-1}+\frac{ bx_{n-1}}{cx_{n-1}-dx_{n-3}}, $ $ n = 0, 1, ..., $ where the initial conditions $ x_{-3, }x_{-2}, \ x_{-1} $and$ x_{0}\ $are arbitrary real numbers and the values $ a, \ b, \ c\ $and$ \;d $ are defined as positive real numbers.
- Stability /
- periodicity /
- global attractor /
- boundedness /
- difference equations
MSC: 39A10

FullText(HTML)

References

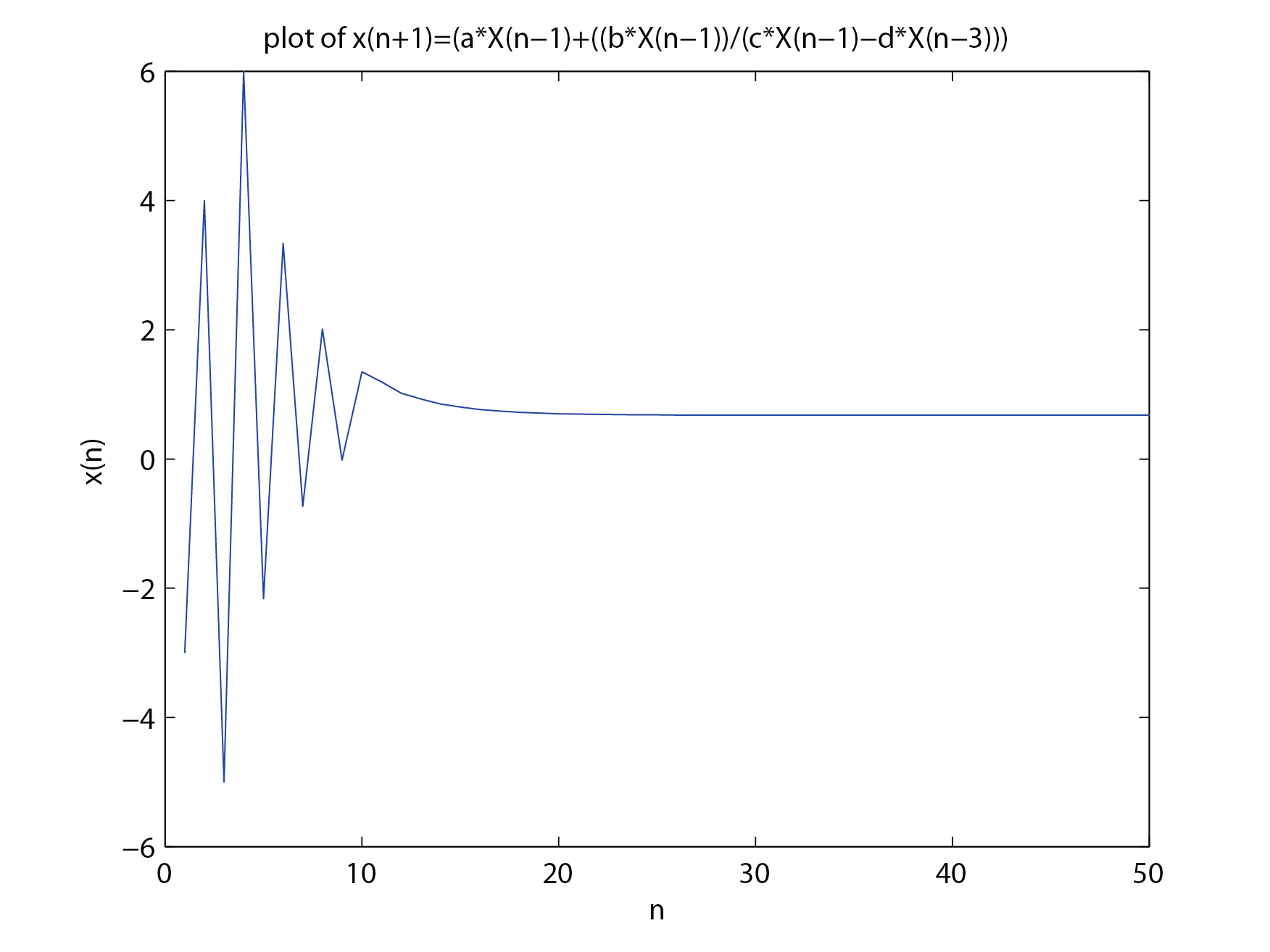
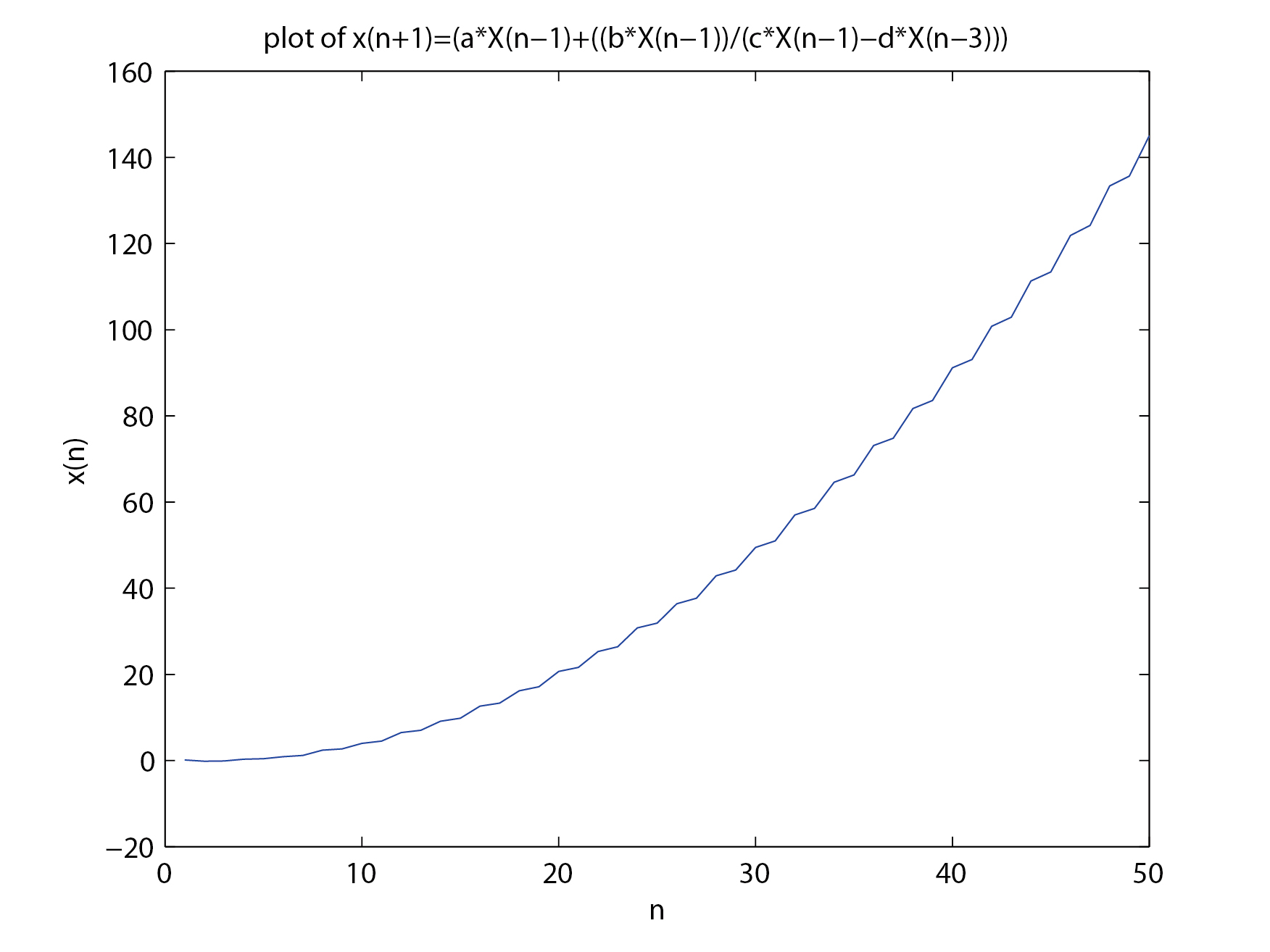
[1]	M. A. E. Abdelrahman and O. Moaaz, On the new class of the nonlinear rational difference equations, Electronic Journal of Mathematical Analysis and Applications, 2018, 6(1), 117–125. Google Scholar
[2]	R. Abo-Zeid and C. Cinar, Global Behavior of The Difference Equation $x_{n+1} = Ax_{n-1}/(B-Cx_{n}x_{n-2}), $ Boletim da Sociedade Paranaense de Matematica, 2013, 31(1), 43–49. Google Scholar
[3]	R. P. Agarwal and E. M. Elsayed, Periodicity and stability of solutions of higher order rational difference equation, Advanced Studies in Contemporary Mathematics, 2008, 17(2), 181–201. Google Scholar
[4]	M. Aloqeili, Dynamics of a Rational Difference Equation, Applied Mathematics and Computation, 2006, 176(2), 768–774. Google Scholar
[5]	F. Belhannache, N. Touafek and R. Abo-zeid, On a Higher-Order Rational Difference Equation, Journal of Applied Mathematics & Informatics, 2016, 34(5–6), 369–382. Google Scholar
[6]	F. Belhannache, Asymptotic stability of a higher order rational difference equation, Electronic Journal of Mathematical Analysis and Applications, 2019, 7(2), 1–8. Google Scholar
[7]	C. Cinar, On The Positive Solutions of The Difference Equation $x_{n+1} = ax_{n-1}/(1+bx_{n}x_{n-1}), $ Applied Mathematics and Computation, 2004, 156, 587–590. doi: 10.1016/j.amc.2003.08.010 CrossRef Google Scholar
[8]	C. Cinar, T. Mansour and, Y Yalçinkaya, On the difference equation of higher order, Utilitas Mathematica, 2013, 92, 161–166. Google Scholar
[9]	E. M. Elabbasy, H. El-Metawally and E. M. Elsayed, On The Difference Equation $x_{n+1} = ax_{n}-bx_{n}/(cx_{n}-dx_{n-1})$, Advances in Difference Equations, 2006, 2006, 1–10. Google Scholar
[10]	E. M. Elabbasy, H. El-Metawally and E. M. Elsayed, On The Difference Equation $x_{n+1} = (ax_{n}.{2}+bx_{n-1}x_{n-k})/(cx_{n}.{2}+dx_{n-1}x_{n-k})$, Sarajevo Journal of Mathematics, 2008, 4(17), 1–10. Google Scholar
[11]	E. M. Elabbasy, H. El-Metawally and E. M. Elsayed, On The Difference Equation $x_{n+1} = (\alpha x_{n-l}+\beta x_{n-k})/(Ax_{n-l}+Bx_{n-k})$, Acta Mathematica Vietnamica, 2008, 33(1), 85–94. Google Scholar
[12]	E. M. Elabbasy and E. M. Elsayed, Global Attractivity and Periodic Nature of a Difference Equation, World Applied Sciences Journal, 2011, 12(1), 39–47. Google Scholar
[13]	M. M. El-Dessoky and M. El-Moneam, On The Higher Order Difference Equation $x_{n+1} = Ax_{n}+Bx_{n-l}+Cx_{n-k}+(\gamma x_{n-k})/(Dx_{n-s}+Ex_{n-t}), $ Journal of Computational Analysis and Applications, 2018, 25(2), 342–354. Google Scholar
[14]	H. El-Metwally and E. M. Elsayed, Solution and Behavior of a Third Rational Difference Equation, Utilitas Mathematica, 2012, 88, 27–42. Google Scholar
[15]	E. M. Elsayed, Behavior and Expression of The Solutions of Some Rational Difference Equations, Journal of Computational Analysis and Applications, 2013, 15(1), 73–81. Google Scholar
[16]	E. M. Elsayed, Dynamics of a Recursive Sequence of Higher Order, Communications on Applied Nonlinear Analysis, 2009, 16(2), 37–50. Google Scholar
[17]	E. M. Elsayed, A. Alghamdi, Dynamics and Global Stability of Higher Order Nonlinear Difference Equation, Journal of Computational Analysis and Applications, 2016, 21(3), 493–503. Google Scholar
[18]	E. M. Elsayed and F. Alzahrani, Periodicity and solutions of some rational difference equations systems, Journal of Applied Analysis and Computation, 2019, 9(6), 2358–2380. doi: 10.11948/20190100 CrossRef Google Scholar
[19]	E. M. Elsayed, F. Alzahrani, I. Abbas and N. H. Alotaibi, Dynamical Behavior and Solution of Nonlinear Difference Equation Via Fibonacci Sequence, Journal of Applied Analysis and Computation, 2020, 10(1), 282–296. doi: 10.11948/20190143 CrossRef Google Scholar
[20]	E. M. Elsayed, F. Alzahrani and H. S. Alayachi, Formulas and Properties of some Class of Nonlinear Difference Equation, Journal of Computational Analysis and Applications, 2018, 4(1), 141–155. Google Scholar
[21]	E. M. Elsayed and M. Alzubaidi, The form of the solutions of system of rational difference equation, Journal of Mathematical Sciences and Modelling, 2018, 1(3), 181–191. Google Scholar
[22]	E. M. Elsayed, S. R. Mahmoud and A. T. Ali, Expression and Dynamics of The Solutions of Some Rational Recursive Sequences, Iranian Journal of Science & Technology, 2014, 38(A3), 295–303. Google Scholar
[23]	M. Gumus, Global Dynamics of Solutions of A New Class of Rational Difference Equations, Konuralp Journal of Mathematics, 2019, 7(2), 380–387. Google Scholar
[24]	T. F. Ibrahim, Generalized partial ToDD's difference equation in n-dimensional space, Journal of Computational Analysis and Applications, 2019, 26(5), 910–926. Google Scholar
[25]	T. F. Ibrahim, On The Third Order Rational Difference Equation $x_{n+1} = (x_{n}x_{n-2})/(x_{n-1}(a+bx_{n}x_{n-2})), $ International Journal of Contemporary Mathematical Sciences, 2009, 4(27), 1321–1334. Google Scholar
[26]	R. Karatas, Global Behavior of a Higher Order Difference Equation, International Journal of Contemporary Mathematical Sciences, 2017, 12(3), 133–138. Google Scholar
[27]	A. Khaliq, F. Alzahrani and E. M. Elsayed, Global Attractivity of a Rational Difference Equation of Order Ten, Journal of Nonlinear Sciences and Applications, 2016, 9, 4465–4477. doi: 10.22436/jnsa.009.06.85 CrossRef Google Scholar
[28]	A. Khaliq and E. Elsayed, The Dynamics and Solution of Some Difference Equations, Journal of Nonlinear Sciences and Applications, 2016, 9(3), 1052–1063. doi: 10.22436/jnsa.009.03.33 CrossRef Google Scholar
[29]	Y. Kostrov, On a Second-Order Rational Difference Equation with a Quadratic Term, International Journal of Difference Equations, 2016, 11(2), 179–202. Google Scholar
[30]	M. R. S. Kulenovic and G. Ladas, Dynamics of Second Order Rational Difference Equations with Open Problems and Conjectures, Chapman & Hall / CRC Press, 2001. Google Scholar
[31]	I. Okumus and Y. Soykan, On the Solutions of Four Second-Order Nonlinear Difference Equations, Universal Journal of Mathematics and Applications, 2019, 2(3), 116–125. Google Scholar
[32]	M. Saleh and M. Aloqeili, On The Difference Equation $y_{n+1} = A+\frac{y_{n}}{y_{n-k}}$, Applied Mathematics and Computation, 2006, 176(1), 359–363. Google Scholar
[33]	S. Sadiq and M. Kalim, Global attractivity of a rational difference equation of order twenty, International Journal of Advanced and Applied Sciences, 2018, 5(2), 1–7. doi: 10.21833/ijaas.2018.02.001 CrossRef Google Scholar
[34]	D. Simsek, C. Cinar and I. Yalcinkaya, On The Recursive Sequence $x_{n+1} = \frac{x_{n-3}}{1+x_{n-1}}$, International Journal of Contemporary Mathematical Sciences, 2006, 1(10), 475–480. Google Scholar
[35]	P. Esengul, Solutions of the Rational Difference Equations, MANAS Journal of Engineering, 2018, 6(2), 177–192. Google Scholar
[36]	Y. Su and W. Li, Global Asymptotic Stability of a Second-Order Nonlinear Difference Equation, Applied Mathematics and Computation, 2005, 168, 981–989. doi: 10.1016/j.amc.2004.09.040 CrossRef Google Scholar
[37]	D. T. Tollu and İ. Yalçı nkaya, Global behavior of a three-dimensional system of difference equations of order three, Communications Faculty of Sciences University of Ankara Series A1 Mathematics and Statistics, 2019, 68(1), 1–16. Google Scholar
[38]	D. T. Tollu, Y. Yazlik, N. Taskara, Behavior of Positive Solutions of a Difference Equation, Journal of Applied Mathematics & Informatics, 2017, 35(3–4), 217–230. Google Scholar
[39]	X. Yang, W. Su, B. Chen, G. M. Megson and D. J. Evans, On The Recursive Sequence $x_{n+1} = (ax_{n-1}+bx_{n-2})/(c+dx_{n-1}x_{n-2}), $ Applied Mathematics and Computation, 2005, 162, 1485–1497. doi: 10.1016/j.amc.2004.03.023 CrossRef Google Scholar
[40]	Y. Yazlik and M. Kara, On a solvable system of difference equations of higher-order with period two coefficients, Communications Faculty of Sciences University of Ankara Series A1 Mathematics and Statistics, 2019, 68(2), 1675–1693. doi: 10.1155/2008/805460 CrossRef Google Scholar
[41]	E. Zayed and M. El-Moneam, On The Rational Recursive Sequence $x_{n+1} = Ax_{n}+Bx_{n-k}+(\beta x_{n}+\gamma x_{n-k})/(Cx_{n}+Dx_{n-k}), $ Acta Applicandae Mathematicae, 2010, 111(3), 287–301. doi: 10.1007/s10440-009-9545-y CrossRef Google Scholar