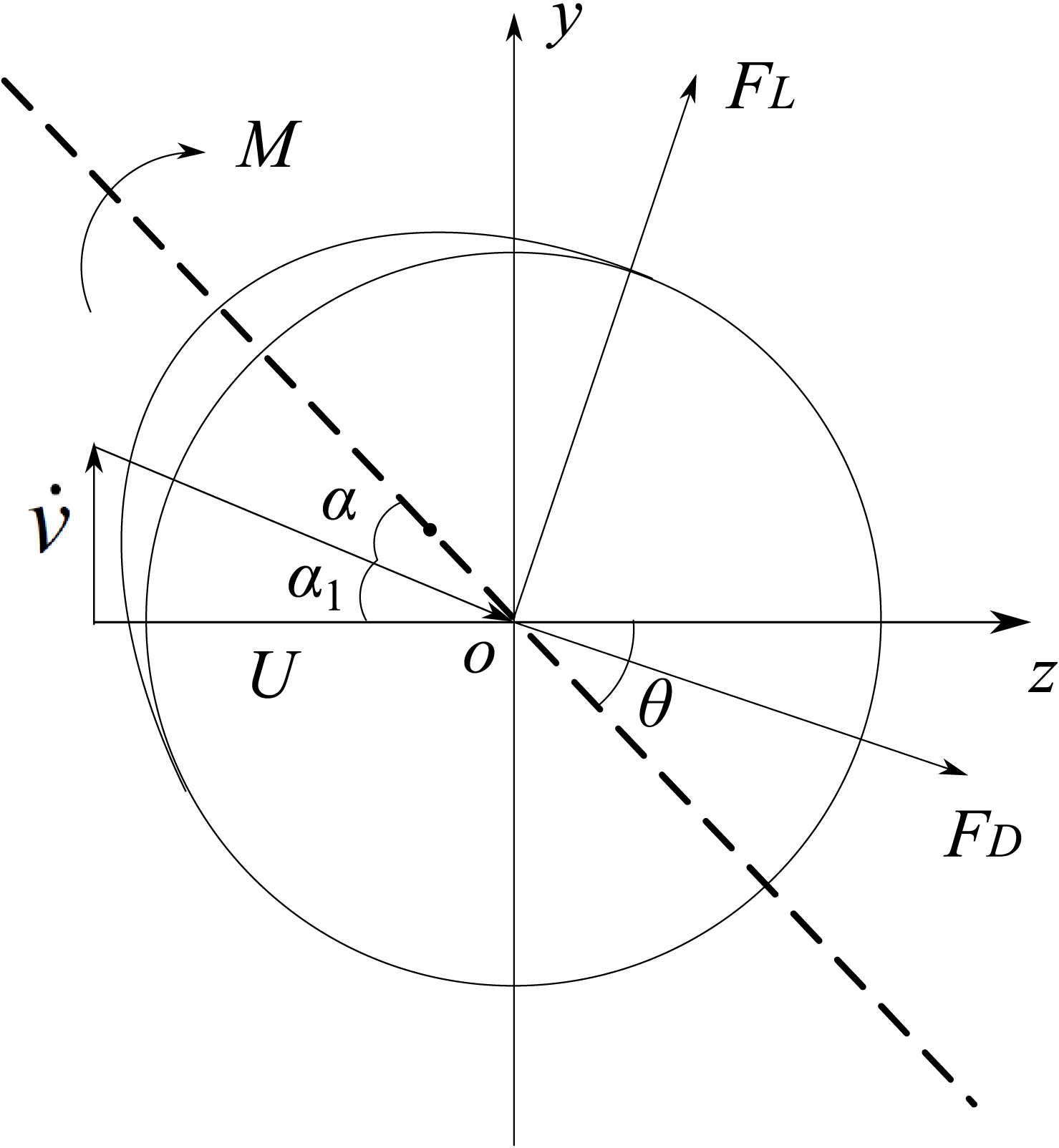
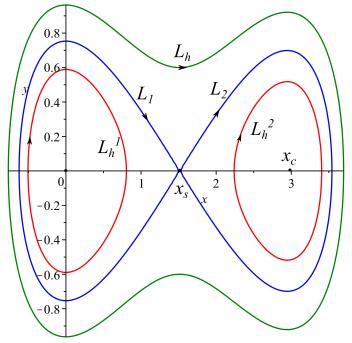
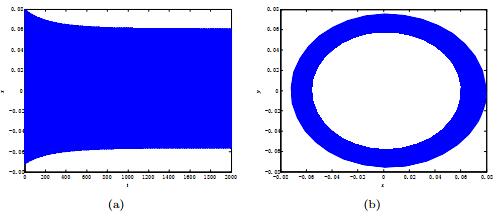
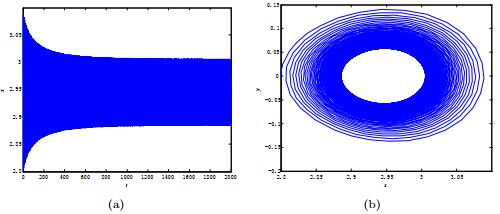
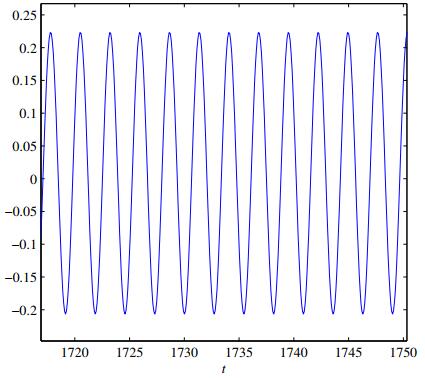
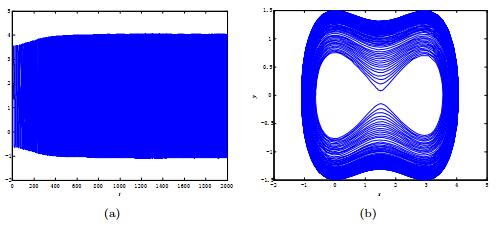
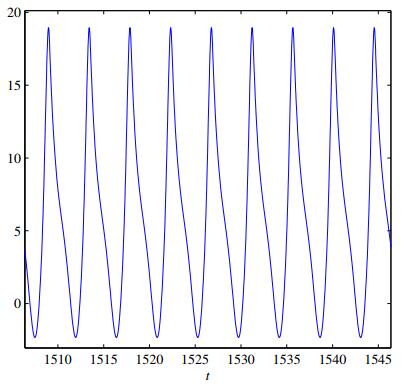
|
[1]
|
V. I. Arnold, Geometrical methods in the theory of ordinary differential equations, 250, Springer Science & Business Media, New York, 2012.
Google Scholar
|
|
[2]
|
J. Den Hartog, Transmission line vibration due to sleet, Transactions of the American Institute of Electrical Engineers, 1932, 4(51), 1074–1076.
Google Scholar
|
|
[3]
|
M. Han, H. Yan, J. Yang and C. Lhotka, On the number of limit cycles of some liénard systems, Canadian Applied Mathematics Quarterly, 2009, 17(1), 61–83.
Google Scholar
|
|
[4]
|
M. Han and P. Yu, Normal forms, Melnikov functions and bifurcations of limit cycles, 181, Springer Science & Business Media, London, 2012.
Google Scholar
|
|
[5]
|
D. Hilbert, Mathematical problems, Bulletin of the American Mathematical Society, 1902, 8, 437–479. doi: 10.1090/S0002-9904-1902-00923-3
CrossRef Google Scholar
|
|
[6]
|
L. Hou and Y. Chen, Study on chaos in galloping of the transmission line, Journal of Vibration Engineering, 2014, 27(1), 75–83.
Google Scholar
|
|
[7]
|
Y. Hou and M. Han, Melnikov functions for planar near-hamiltonian systems and hopf bifurcations, Journal of Shanghai Normal University(Natural Science), 2006, 35(1), 1–10.
Google Scholar
|
|
[8]
|
B. Liu, K. Zhu, X. Li and X. Zhan, Hysteresis phenomenon in the galloping of the d-shape iced conductor, Mathematical Problems in Engineering, 2013, 784239.
Google Scholar
|
|
[9]
|
B. Liu, K. Zhu, X. Sun et al., A contrast on conductor galloping amplitude calculated by three mathematical models with different dofs, Shock and Vibration, 2014, 2014, 781304.
Google Scholar
|
|
[10]
|
F. Liu, Q. Zhang and Y. Tan, Analysis of high codimensional bifurcation and chaos for the quad bundle conductor's galloping, Chinese Physics Letters, 2010, 27(4), 044702. doi: 10.1088/0256-307X/27/4/044702
CrossRef Google Scholar
|
|
[11]
|
X. Liu and B. Huo, Nonlinear vibration and multimodal interaction analysis of transmission line with thin ice accretions, International Journal of Applied Mechanics, 2015, 7(01), 1550007. doi: 10.1142/S1758825115400074
CrossRef Google Scholar
|
|
[12]
|
Y. Liu and Y. Chen, Global bifurcations for a generalized codimension-4 duffing-van der pol equation, Journal of Vibration and Shock, 2011, 30(1), 69–72.
Google Scholar
|
|
[13]
|
A. Luongo, D. Zulli and G. Piccardo, A linear curved-beam model for the analysis of galloping in suspended cables, Journal of Mechanics of Materials and Structures, 2007, 2(4), 675–694. doi: 10.2140/jomms.2007.2.675
CrossRef Google Scholar
|
|
[14]
|
A. Luongo, D. Zulli and G. Piccardo, Analytical and numerical approaches to nonlinear galloping of internally resonant suspended cables, Journal of Sound and Vibration, 2008, 315(3), 375–393. doi: 10.1016/j.jsv.2008.03.067
CrossRef Google Scholar
|
|
[15]
|
P. McComber and A. Paradis, A cable galloping model for thin ice accretions, Atmospheric Research, 1998, 46(1), 13–25.
Google Scholar
|
|
[16]
|
S. Meng and W. Kong, Design of Overhead Transmission Line, China Electric Power Press, Beijing, 2007.
Google Scholar
|
|
[17]
|
O. Nigol and P. Buchan, Conductor galloping part i-den hartog mechanism, IEEE transactions on power apparatus and systems, 1981, 2(PAS-100), 699–707.
Google Scholar
|
|
[18]
|
O. Nigol and P. Buchan, Conductor galloping-part ii torsional mechanism, IEEE Transactions on Power Apparatus and Systems, 1981, 2(PAS-100), 708–720.
Google Scholar
|
|
[19]
|
Z. Qin, Y. Chen, X. Zhan et al., Research on the galloping and anti-galloping of the transmission line, International Journal of Bifurcation and Chaos, 2012, 22(02), 1250038. doi: 10.1142/S0218127412500381
CrossRef Google Scholar
|
|
[20]
|
X. Sun, P. Yu and Q. Bin, Global existence and uniqueness of periodic waves in a population model with density-dependent migrations and allee effect, International Journal of Bifurcation and Chaos, 2017, 27(12), 1750192. doi: 10.1142/S0218127417501929
CrossRef Google Scholar
|
|
[21]
|
Z. Yan, Z. Yan, Z. Li and T. Tan, Nonlinear galloping of internally resonant iced transmission lines considering eccentricity, Journal of Sound and Vibration, 2012, 331(15), 3599–3616. doi: 10.1016/j.jsv.2012.03.011
CrossRef Google Scholar
|
|
[22]
|
P. Yu, A. Shah and N. Popplewell, Inertially coupled galloping of iced conductors, Journal of applied mechanics, 1992, 59(1), 140–145. doi: 10.1115/1.2899419
CrossRef Google Scholar
|
|
[23]
|
Q. Zhang, N. Popplewell and A. Shah, Galloping of bundle conductor, Journal of Sound and Vibration, 2000, 234(1), 115–134.
Google Scholar
|




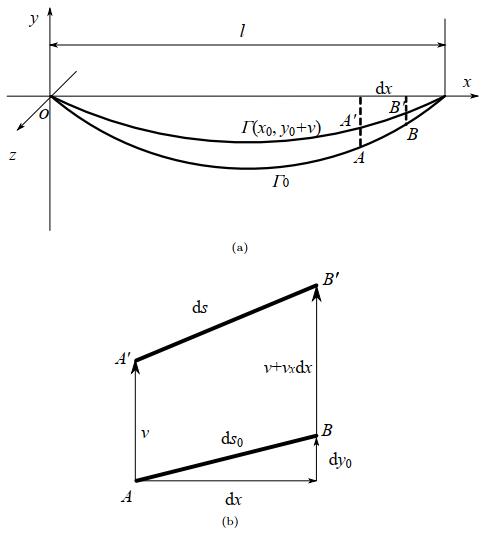

 DownLoad:
DownLoad: