| Citation: |
Shohel Ahmed, Md. Kamrujjaman, Sumaiya Rahman. DYNAMICS OF A VIRAL INFECTIOLOGY UNDER TREATMENT[J]. Journal of Applied Analysis & Computation, 2020, 10(5): 1800-1822. doi: 10.11948/20190209
|
DYNAMICS OF A VIRAL INFECTIOLOGY UNDER TREATMENT
-
Abstract
This paper deals with a nonlinear model of the viral dynamics which describes the interactions between the human immune system and the virus. The novelty of this work is the introduction of combined treatments in the dynamics to modify the model. We investigate the qualitative behavior of the model and find a threshold parameter that guarantees the asymptotic stability of the equilibrium points, this parameter is known as the basic reproduction number. We estimated the parameters of the model by least-squares minimization between the numerical solution of the system and clinical data of cell cultures. It is also demonstrated that critical drug efficacy in terms of the model parameter is greatly useful to curtail the spreading of the disease. -
-
References
[1] D. S. Callaway and A. S. Perelson, HIV-1 infection and low steady state viral loads, Bulletin of Mathematical Biology, 2002, 64(4), 29-64. [2] A. R. M. Carvalho and C. M. A. Pintoi, Contributions of the latent reservoir and of the pool of long –lived chronically infected CD4$^+$T cells in HIV dynamics: a fractional approach, Proceedings of the ENOC2017, June, 2017. [3] O. Diekmann, J. A. P. Heesterbeek and J. A. J. Metz, On the definition and the computation of the basic reproduction ratio $R_0$ in models for infectious diseases in heterogeneous populations, Journal of Mathematical Biology, 1990, 28, 365-382. $R_0$ in models for infectious diseases in heterogeneous populations" target="_blank">Google Scholar
[4] A. M. Elaiw, Global properties of a class of HIV models, Nonlinear Analysis: Real World Applications, 2010, 11, 2253-2263. doi: 10.1016/j.nonrwa.2009.07.001 [5] A. M. Elaiw, T. O. Alade and S. M. Alsulami, Analysis of latent CHIKV dynamics models with general incidence rate and time delays, Journal of Biological Dynamics, 2018, 12(1), 700-730. doi: 10.1080/17513758.2018.1503349 [6] A. M. Elaiw, T. O. Alade and S. M. Alsulami, Analysis of within-host CHIKV dynamics models with general incidence rate, International Journal of Biomathematics, 2018, 11(5). Article Number: 1850062. [7] A. M. Elaiw and N. H. AlShamrani, Stability of an adaptive immunity pathogen dynamics model with latency and multiple delays, Mathematical Methods in the Applied Science, 2018, 36, 125-142. [8] A. M. Elaiw, A. A. Raezah and S. A. Azoz, Stability of delayed HIV dynamics models with two latent reservoirs and immune impairment, Advances in Difference Equations, 2018, 2018:414. doi: 10.1186/s13662-018-1869-3 [9] S. Engelberg, A Mathematical Introduction to Control Theory, World Scientific Publishing Company, 2015. [10] L. Gibelli, A. M. Elaiw, M. A. Alghamdi and A. M. Althiabi, Heterogeneous population dynamics of active particles: Progression, mutations, and selection dynamics, Mathematical Models and Methods in Applied Sciences, 2017, 27, 617-640. doi: 10.1142/S0218202517500117 [11] P. Hartman, A lemma in the theory of structural stability of differential equation, Proceedings of the American Mathematical Society, 1960, 11, 610-620. doi: 10.1090/S0002-9939-1960-0121542-7 [12] J. M. Heffernan, R. J. Smith and L. M. Wahl, Perspectives on the basic reproductive ratio, Journal of Royal Society, 2005, 2, 281-293. [13] T. Kajiwara, T. Sasaki and Y. Takeuchi, Construction of Lyapunov functionals for delay differential equations in Virology and Epidemiology, Nonlinear Analysis: Real World Applications, 2012, 13, 1802-1826. doi: 10.1016/j.nonrwa.2011.12.011 [14] W. G. Kelley and A. C. Peterson, The Theory of Differential Equations, Springer, New York, 2010. [15] J. Lasalle, The Stability of Dynamical Systems, SIAM, Philadelphia, 1976. [16] S. Lenhart and J. Workman, Optimal Control Applied to Biological Models, Chapman & Hall/CRC Mathematical and Computational Biology, CRC Press, 2007. [17] M. A. Nowak and R. May, Virus dynamics: Mathematical principles of Immunology and Virology, Oxford University Press, Oxford, 2000. [18] P. Paci, R. Carello, M. Bernaschi et al., Immune control of HIV-1 infection after therapy interruption: immediate versus deferred antiretroviral therapy, BMS Infections Diseases, 2009, 9, 1-13. doi: 10.1186/1471-2334-9-1 [19] A. S. Perelson, D. E. Kirschner and R. d. Boer, Dynamics of HIV infection of CD4$^+$T cells, Mathematical Biosciences, 1993, 114, 81-125. [20] M. H. Protter and H. F. Weinberger, Maximum Principles in Differential Equations, Springer, New York, 1999. [21] R. M. Ribeiro, L. Qin, L. L. Chavez et al., Estimation of the initial viral growth rate and basic reproductive number during acute HIV-1 infection, Journal of Virology, 2010, 12, 6096-102. [22] M. A. Stafford, L. Corey, Y. Cao et al., Estimation of HIV/AIDS parameters, Automatica, 2003, 39, 1983-1988. doi: 10.1016/S0005-1098(03)00220-6 [23] M. A. Stafford, L. Corey, Y. Cao et al., Modeling plasma virus concentration during primary HIV infection, Journal of Theoretical Biology, 2010, 203, 285-301. [24] K. Wang, A. Fan and A. Torres, Global properties of an improved Hepatitis B virus model, Nonlinear Analysis: Real World Applications, 2010, 11, 3131-3138. doi: 10.1016/j.nonrwa.2009.11.008 -
-
Figures(9) / Tables(1)
Export File
Citation
Shohel Ahmed, Md. Kamrujjaman, Sumaiya Rahman. DYNAMICS OF A VIRAL INFECTIOLOGY UNDER TREATMENT[J]. Journal of Applied Analysis & Computation, 2020, 10(5): 1800-1822. doi: 10.11948/20190209
Format
Content
DownLoad:
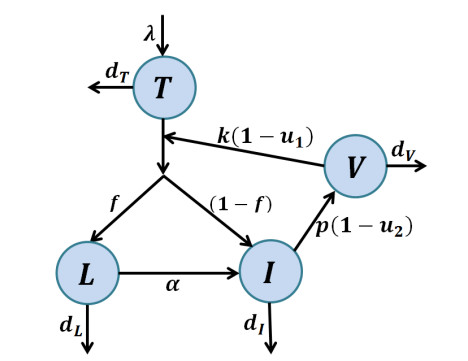
- Figure 1. Schematic diagram of viral kinetic model with the combination of treatments.
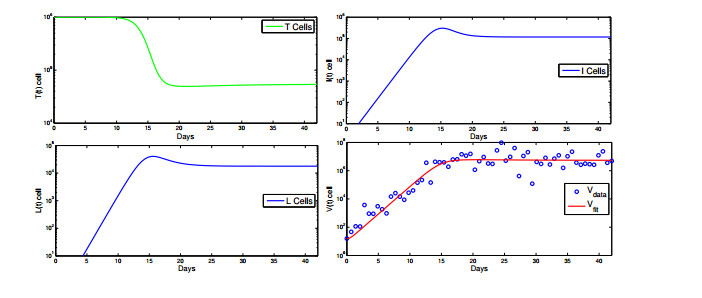
- Figure 2. Dynamics and data fitting of model (2.1) in Semi-log scale.
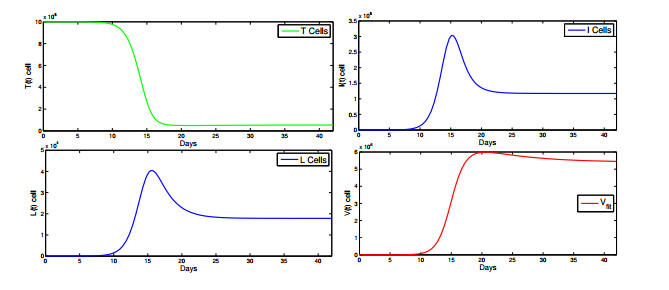
- Figure 3. Dynamics of model (2.1) in normal scale.
-
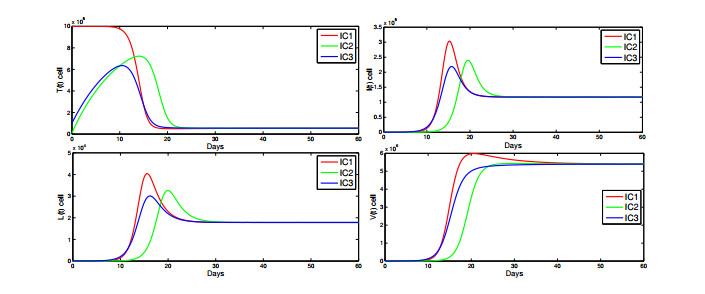
Figure 4. Dynamics of Model (2.1) for
$ R_L = 18.37 > 1 $ with three different intial conditions. -
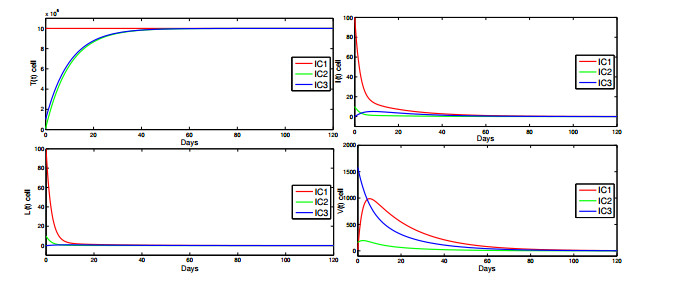
Figure 5. Dynamics of Model (2.1) for
$ R_L = 0.57 < 1 $ with three different intial conditions. -
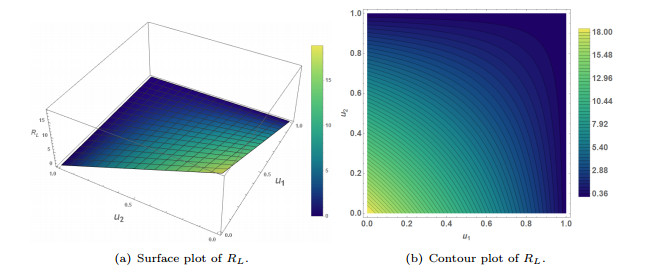
Figure 6. Surface and contour plot of
$ R_L $ for various values of$ u_1 $ and$ u_2 $ . -
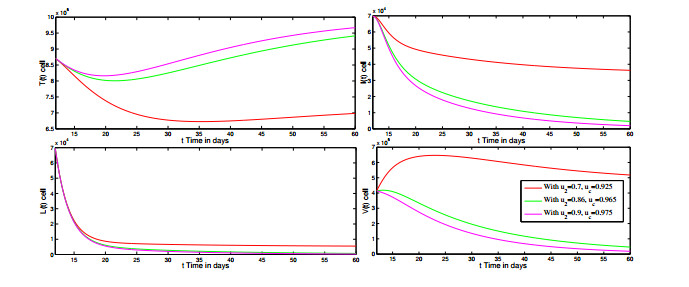
Figure 7. Cell dynamics during various values of
$ u_2 $ with fix$ u_1 = 0.75 $ . -
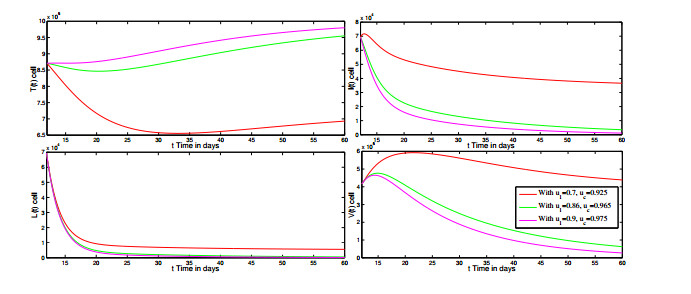
Figure 8. Cell dynamics during various values of
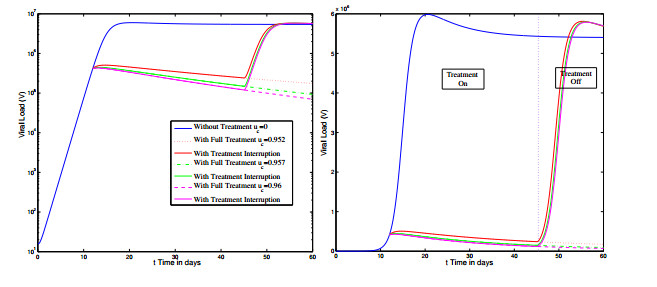
$ u_1 $ with fix$ u_2 = 0.75 $ . - Figure 9. Pattern of viral load with an on-off treatment with the treatment being administered for 45 days and then the treatment being interrupted for the next 15 days.