|
[1]
|
A. Berman and R. J. Plemmons, Nonnegative matrices in mathematical sciences, Academic Press, New York, 1979.
Google Scholar
|
|
[2]
|
N. P. Bhatia and G. P. Szego, Dynamical systems: stability theory and applications, Lecture Notes in Mathematics, Springer, Berlin, 1967.
Google Scholar
|
|
[3]
|
C. Castillo-Chavez and H. R. Thieme, Asymptotically autonomous epidemic models, Mathematical Population Dynamics: Analysis and Heterogeneity. Volume One: Theory of epidemics, Wuerz Publishing Ltd, Winnipeg, 1995.
Google Scholar
|
|
[4]
|
C. Dai, A. Fan and K. Wang, Transmission dynamics and the control of hepatitis B in China: a population dynamics view, J. Appl. Anal. Comput., 2016, 6(1), 76-93.
Google Scholar
|
|
[5]
|
M. C. Eisenberg, Z. Shuai, J. H. Tien and et al., A cholera model in a patchy environment with water and human movement, Math. Biosci., 2013, 246(1), 105-112.
Google Scholar
|
|
[6]
|
A. M. Fink, Almost periodic differential equations, 377 of Lecture Notes in Mathematics, Springer-Verlag, New York, 1974.
Google Scholar
|
|
[7]
|
H. I. Freedman, S. Ruan and M. Tang, Uniform persistence and flows near a closed positively invariant set, J. Dynam. Differential Equations, 1994, 6(4), 583-600. doi: 10.1007/BF02218848
CrossRef Google Scholar
|
|
[8]
|
R. Gorenflo, A. A. Kilbas, F. Mainardi and et al., Mittag-Leffler functions, related topics and applications, Springer Monographs in Mathematics, Springer, Berlin, 2014.
Google Scholar
|
|
[9]
|
Q. Huan, P. Ning and W. Ding, Global stability for a dynamic model of hepatitis B with antivirus treatment, J. Appl. Anal. Comput., 2013, 3(1), 37-50.
Google Scholar
|
|
[10]
|
C. Huang, Y. Qiao, L. Huang and et al., Dynamical behaviors of a food-chain model with stage structure and time delays, Adv. Difference Equ., 2018, 2018, 186. doi: 10.1186/s13662-018-1589-8
CrossRef Google Scholar
|
|
[11]
|
C. Huang, R. Su, J. Cao and et al., Asymptotically stable high-order neutral cellular neural networks with proportional delays and D operators, Math. Comput. Simulation, 2020, 171, 127-135. doi: 10.1016/j.matcom.2019.06.001
CrossRef Google Scholar
|
|
[12]
|
C. Huang, H. Zhang, J. Cao and et al., Stability and Hopf bifurcation of a delayed prey-predator model with disease in the predator, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2019, 29(7), 1950091. doi: 10.1142/S0218127419500913
CrossRef Google Scholar
|
|
[13]
|
C. Huang, H. Zhang and L. Huang, Almost periodicity analysis for a delayed Nicholson's blowflies model with nonlinear density-dependent mortality term, Commun. Pure Appl. Anal., 2019, 18(6), 3337-3349. doi: 10.3934/cpaa.2019150
CrossRef Google Scholar
|
|
[14]
|
K. E. Jones, N. G. Patel, M. A. Levy and et al., Global trends in emerging infectious diseases, Nature, 2008, 451, 990-993. doi: 10.1038/nature06536
CrossRef Google Scholar
|
|
[15]
|
A. V. Kamyad, R. Akbari, A. A. Heydari and et al., Mathematical modeling of transmission dynamics and optimal control of vaccination and treatment for hepatitis B virus, Comput. Math. Methods Med., 2014. DOI: 10.1155/2014/475451.
CrossRef Google Scholar
|
|
[16]
|
M. A. Khan, S. Islam and G. Zaman, Media coverage campaign in hepatitis B transmission model, Appl. Math. Comput., 2018, 331, 378-393.
Google Scholar
|
|
[17]
|
T. Khan, G. Zaman and M. I. Chohan, The transmission dynamic and optimal control of acute and chronic hepatitis B, J. Biol. Dyn., 2016, 11(1), 172-189.
Google Scholar
|
|
[18]
|
M. Kot, Elements of mathematical ecology, Cambridge University Press, Cambridge, 2001.
Google Scholar
|
|
[19]
|
Y. Li and T. Zhang, Existence and multiplicity of positive almost periodic solutions for a non-autonomous SIR epidemic model, Bull. Malays. Math. Sci. Soc., 2016, 39(1), 359-379. doi: 10.1007/s40840-015-0176-3
CrossRef Google Scholar
|
|
[20]
|
P. Liu, L. Zhang, S. Liu and et al., Global exponential stability of almost periodic solutions for Nicholson's blowflies system with nonlinear density dependent mortality terms and patch structure, Math. Model. Anal., 2017, 22(4), 484-502.
Google Scholar
|
|
[21]
|
Y. Muroya, T. Kuniya and J. Wang, Stability analysis of a delayed multi-group SIS epidemic model with nonlinear incidence rates and patch structure, J. Math. Anal. Appl., 2015, 425(1), 415-439. doi: 10.1016/j.jmaa.2014.12.019
CrossRef Google Scholar
|
|
[22]
|
Polaris Observatory Collaborators, Global prevalence, treatment, and prevention of hepatitis B virus infection in 2016: a modelling study, Lancet Gastroenterol Hepatol., 2018, 3, 383-403.
Google Scholar
|
|
[23]
|
S. Ruan, W. Wang and A. L. Simon, The effect of global travel on the spread of SARS, Math. Biosci. Eng., 2006, 3(1), 205-218. doi: 10.3934/mbe.2006.3.205
CrossRef Google Scholar
|
|
[24]
|
H. L. Smith and P. Waltman, The theory of the chemostat: dynamics of microbial competition, Cambridge studies in mathematical biology, Cambridge University Press, Cambridge, 1995.
Google Scholar
|
|
[25]
|
H. R. Thieme, Convergence results and a Poincaré-Bendixson trichotomy for asymptotically autonomous differential equations, J. Math. Biol., 1992, 30(7), 755-763.
Google Scholar
|
|
[26]
|
J. P. Tripathi and S. Abbas, Global dynamics of autonomous and nonautonomous SI epidemic models with nonlinear incidence rate and feedback controls, Nonlinear Dynam., 2016, 86(1), 337-351. doi: 10.1007/s11071-016-2892-0
CrossRef Google Scholar
|
|
[27]
|
S. Ullah, M. A. Khan and M. Farooq, A new fractional model for the dynamics of the hepatitis B virus using the Caputo-Fabrizio derivative, Eur. Phys. J. Plus, 2018, 133(6). Article-Number: 237.
Google Scholar
|
|
[28]
|
S. Ullah, M. A. Khan and M. Farooq, Modeling and analysis of the fractional HBV model with Atangana-Baleanu derivative, Eur. Phys. J. Plus, 2018, 133(8). Article-Number: 313.
Google Scholar
|
|
[29]
|
S. Ullah, M. A. Khan and J. F. Gomez-Aguilar, Mathematical formulation of hepatitis B virus with optimal control analysis, Optimal Control Appl. Methods, 2019, 40(3), 529-544. doi: 10.1002/oca.2493
CrossRef Google Scholar
|
|
[30]
|
P. Van den Driessche and J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Math. Biosci., 2002, 180(1-2), 29-48. doi: 10.1016/S0025-5564(02)00108-6
CrossRef Google Scholar
|
|
[31]
|
B. Wang and X. Zhao, Basic reproduction ratios for almost periodic compartmental epidemic models, J. Dynam. Differential Equations, 2013, 25(2), 535-562. doi: 10.1007/s10884-013-9304-7
CrossRef Google Scholar
|
|
[32]
|
J. Wang and X. Tian, Global stability of a delay differential equation of hepatitis B virus infection with immune response, Electron. J. Differential Equations, 2013, 2013(94), 204-220.
Google Scholar
|
|
[33]
|
W. Wang and X. Zhao, An epidemic model in a patchy environment., Math. Biosci., 2004, 190(1), 97-112.
Google Scholar
|
|
[34]
|
X. Wang, Z. Yang and X. Liu, Periodic and almost periodic oscillations in a delay differential equation system with time-varying coefficients, Discrete Contin. Dyn. Syst., 2017, 37(12), 6123-6138. doi: 10.3934/dcds.2017263
CrossRef Google Scholar
|
|
[35]
|
Y. Wang, Asymptotic state of a two-patch system with infinite diffusion, Bull. Math. Biol., 2019, 81(6), 1665-1686. doi: 10.1007/s11538-019-00582-4
CrossRef Google Scholar
|
|
[36]
|
J. Zhang and S. Zhang, Application and optimal control for an HBV model with vaccination and treatment, Discrete Dyn. Nat. Soc., 2018. DOI: 10.1155/2018/2076983.
CrossRef Google Scholar
|




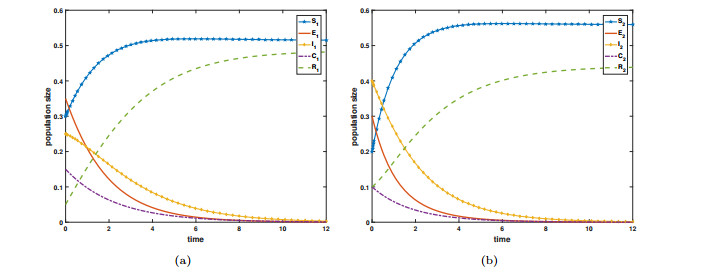

 DownLoad:
DownLoad: