| Citation: | Shina D. Oloniiju, Sicelo P. Goqo, Precious Sibanda. A GEOMETRICALLY CONVERGENT PSEUDO–SPECTRAL METHOD FOR MULTI–DIMENSIONAL TWO–SIDED SPACE FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 1699-1717. doi: 10.11948/20200023 |
A GEOMETRICALLY CONVERGENT PSEUDO–SPECTRAL METHOD FOR MULTI–DIMENSIONAL TWO–SIDED SPACE FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS
-
Abstract
In this study, we present a geometrically convergent numerical method for solving multi-dimensional two-sided space-time fractional differential equations. The approach represents the solutions of the differential equations in terms of the shifted Chebyshev polynomials. The expansions are evaluated at the shifted Chebyshev-Gauss-Lobatto nodes. We present the approximations for left-sided integration, and the left- and right- sided differentiation. The performance of the method is demonstrated using some two-sided space fractional partial differential equations in one and two dimensions. The numerical results obtained show that the method is accurate and computationally efficient. A theoretical analysis of the convergence of the method is presented, where it is shown that, given a continuously differentiable solution, the numerical solution converges for a sufficiently large number of grid points.
-

-
References
[1] M. Abramowitz and I. A. Stegun, Handbook of mathematical functions: with formulas, graphs, and mathematical tables, Courier Corporation, Mas-sachusetts, 1965. [2] D. A. Benson, M. M. Meerschaert and J. Revielle, Fractional calculus in hy-drologic modeling: A numerical perspective, Adv. Water Resour., 2013, 51, 479-497. doi: 10.1016/j.advwatres.2012.04.005 [3] A. Bhrawy and M. Zaky, Shifted fractional-order Jacobi orthogonal functions: application to a system of fractional differential equations, Appl. Math. Model., 2016, 40(2), 832-845. doi: 10.1016/j.apm.2015.06.012 [4] A. Bhrawy, M. A. Zaky and R. A. Van Gorder, A space-time Legendre spec-tral tau method for the two-sided space-time Caputo fractional diffusion-wave equation, Numer. Algorithms, 2016, 71(1), 151-180. doi: 10.1007/s11075-015-9990-9 [5] A. H. Bhrawy, M. A. Zaky and J. A. T. Machado, Numerical solution of the two-sided space-time fractional telegraph equation via Chebyshev tau approximation, J. Optim. Theory Appl., 2017, 174(1), 321-341. doi: 10.1007/s10957-016-0863-8 [6] H. Bulut, H. M. Baskonus and Y. Pandir, The modified trial equation method for fractional wave equation and time fractional generalized Burgers equation, Abstract Appl. Anal., 2013. Article ID 636802. [7] C. Canuto, M. Y. Hussaini, A. Quarteroni and T. A. Zang, Spectral methods: Fundametals in single domains, Springer, New York, 2006. [8] C. Canuto, M. Y. Hussaini, A. Quarteroni et al., Spectral methods in fluid dynamics, Springer Science & Business Media, Berlin, 2012. [9] M. Chen and W. Deng, A second-order numerical method for two-dimensional two-sided space fractional convection diffusion equation, Appl. Math. Model., 2014, 38(13), 3244-3259. doi: 10.1016/j.apm.2013.11.043 [10] S. Chen, F. Liu, X. Jiang et al., A fast semi-implicit difference method for a nonlinear two-sided space-fractional diffusion equation with variable diffusivity coefficients, Appl. Math. Comput., 2015, 257, 591-601. [11] R. Cheng, F. Sun and J. Wang, Meshless analysis of two-dimensional two-sided space-fractional wave equation based on improved moving least-squares approximation, Int. J. Comput. Math., 2018, 95(3), 540-560. doi: 10.1080/00207160.2017.1291933 [12] F. del Teso, Finite difference method for a fractional porous medium equation, Calcolo, 2014, 51(4), 615-638. doi: 10.1007/s10092-013-0103-7 [13] M. Diouf and N. Sene, Analysis of the financial chaotic model with the fractional derivative operator, Complexity, 2020, 2020. [14] E. Doha, A. Bhrawy and S. Ezz-Eldien, Efficient Chebyshev spectral methods for solving multi-term fractional orders differential equations, Appl. Math. Model., 2011, 35(12), 5662-5672. doi: 10.1016/j.apm.2011.05.011 [15] L. Feng, P. Zhuang, F. Liu and I. Turner, Stability and convergence of a new finite volume method for a two-sided space-fractional diffusion equation, Appl. Math. Comput., 2015, 257, 52-65. [16] F. Liu, P. Zhuang, V. Anh et al., Stability and convergence of the difference methods for the space-time fractional advection-diffusion equation, Appl. Math. Comput., 2007, 191(1), 12-20. [17] F. Liu, P. Zhuang, I. Turner et al., A semi-alternating direction method for a 2-D fractional FitzHugh-Nagumo monodomain model on an approximate irregular domain, J. Comput. Phys., 2015, 293, 252-263. doi: 10.1016/j.jcp.2014.06.001 [18] F. Mainardi, Fractional calculus and waves in linear viscoelasticity: An intro-duction to mathematical models, World Scientific, Singapore, 2010. [19] Z. Mao and J. Shen, Spectral element method with geometric mesh for two-sided fractional differential equations, Adv. Comput. Math., 2018, 44(3), 745-771. doi: 10.1007/s10444-017-9561-9 [20] M. M. Meerschaert and C. Tadjeran, Finite difference approximations for two-sided space-fractional partial differential equations, Appl. Numer. Math., 2006, 56(1), 80-90. doi: 10.1016/j.apnum.2005.02.008 [21] K. S. Miller and B. Ross, An introduction to the fractional calculus and frac-tional differential equations, Wiley-Interscience, New Jersey, 1993. [22] K. Oldham and J. Spanier, The fractional calculus theory and applications of differentiation and integration to arbitrary order, Elsevier, Amsterdam, 1974. [23] S. Oloniiju, S. Goqo and P. Sibanda, A Chebyshev spectral method for heat and mass transfer in MHD nanofluid flow with space fractional constitutive model, Frontiers in Heat and Mass Transfer, 2019, 13. DOI: 10.5098/hmt.13.19. [24] S. D. Oloniiju, S. P. Goqo and P. Sibanda, A Chebyshev pseudo-spectral method for the multi-dimensional fractional Rayleigh problem for a generalized Maxwell fluid with Robin boundary conditions, Appl. Numer. Math., 2020, 152, 253-266. doi: 10.1016/j.apnum.2019.12.001 [25] Ł. Płociniczak, Analytical studies of a time-fractional porous medium equation. Derivation, approximation and applications, Commun. Nonlinear Sci. Numer. Simul., 2015, 24(1-3), 169-183. doi: 10.1016/j.cnsns.2015.01.005 [26] I. Podlubny, Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications, Elsevier, Amsterdam, 1998. [27] H. Qi and M. Xu, Unsteady flow of viscoelastic fluid with fractional Maxwell model in a channel, Mech. Res. Commun., 2007, 34(2), 210-212. doi: 10.1016/j.mechrescom.2006.09.003 [28] N. Sene, Second-grade fluid model with Caputo-Liouville generalized fractional derivative, Chaos, Solitons & Fractals, 2020, 133, 109631. [29] N. H. Sweilam, M. M. Khader and A. Nagy, Numerical solution of two-sided space-fractional wave equation using finite difference method, J. Comput. Appl. Math., 2011, 235(8), 2832-2841. doi: 10.1016/j.cam.2010.12.002 [30] M. Yavuz and N. Sene, Stability analysis and numerical computation of the fractional predator-prey model with the harvesting rate, Fractal and Fractional, 2020, 4(3), 35. doi: 10.3390/fractalfract4030035 [31] M. A. Zaky, An improved tau method for the multi-dimensional fractional Rayleigh-Stokes problem for a heated generalized second grade fluid, Comput. Math. Appl., 2018, 75(7), 2243-2258. doi: 10.1016/j.camwa.2017.12.004 -
-
-
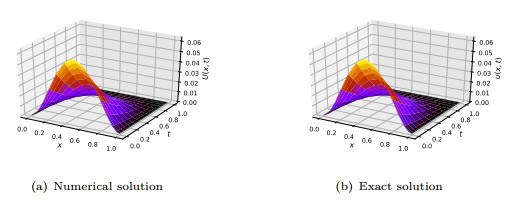
Figure 1. Numerical and exact solutions of Example 5.1. on the temporal and spatial grids for
$ N_x = 16 $ and$ N_t = 16 $ . -
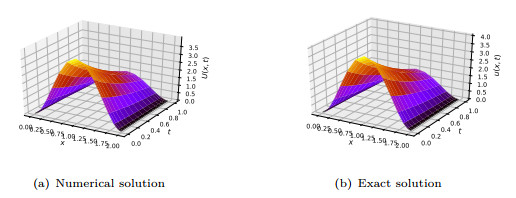
Figure 2. Solutions of Example 5.2 on the spatial-temporal grid for
$ N_x = N_t = 16 $ with$ \gamma = 0.5 $ and$ \alpha = 1.5 $ . -
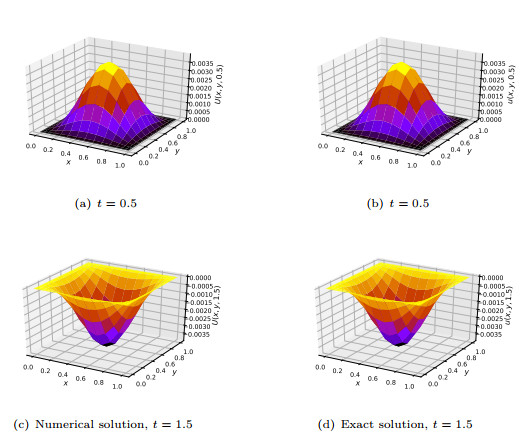
Figure 3. Solutions of Example 5.3 for
$ N_x = N_y = N_t = 16 $ for$ \alpha = \beta = 1.5 $ at$ t = (0.5, 1.5) $ . -
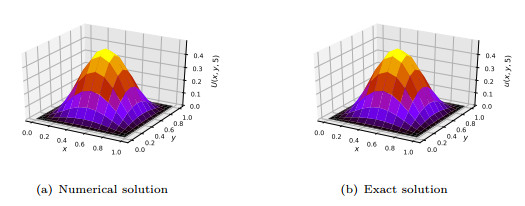
Figure 4. Exact and numerical solutions of Example 5.4 with
$ \gamma = 0.9 $ and$ \alpha = \beta = 1.5 $ at$ t = 5 $ .




 DownLoad:
DownLoad: