| Citation: | Jiaping Yu, Yuhong Zhang. NITSCHE'S TYPE STABILIZATION FOR THE FULLY MIXED NAVIER-STOKES/DARCY PROBLEM[J]. Journal of Applied Analysis & Computation, 2021, 11(3): 1481-1493. doi: 10.11948/20200249 |
NITSCHE'S TYPE STABILIZATION FOR THE FULLY MIXED NAVIER-STOKES/DARCY PROBLEM
-
Abstract
In this paper, we present and analyze a fully mixed finite element scheme for the Navier-Stokes/Darcy problem based on the Nitsche's type interface stabilizations, in the fluid region coupled with the porous media domain. The reasonable parameter $ \delta>0 $, which is independent of mesh size $ h $, will guarantee the stability and optimal convergence of our stabilized scheme. Moreover, we explicitly derive the dependence and requirement of the stabilization parameter $ \delta $ for the optimal error estimates, while the numerical tests support the stability and efficiency of this stabilized mixed method.
-

-
References
[1] R. A. Adams and J. J. F. Fournier, Sobolev Spaces, 2nd ed., Elsevier/Academic Press, Amsterdam, Pure Appl. Math. (Amst. ), 2003, 140. [2] F. Brezzi and M. Fortin, Mixed and Hybrid Finite Element Methods, In: Springer Series in Computational Mathematics, vol. 15, Springer-Verlag, New York, 1991. [3] E. Burman and P. Hansbo, A unified stabilized method for Stokes' and Darcy's equations, J. Comput. Appl. Math., 2007, 198, 35-51. doi: 10.1016/j.cam.2005.11.022 [4] A. Bastide, P. H. Cocquet and D. Ramalingom, Penalization model for Navier-Stokes-Darcy equations with application to porosity-oriented topology optimization, Math. Models Methods Appl. Sci., 2018, 28(8), 1481-1512. doi: 10.1142/S0218202518500409 [5] M. Cai, M. Mu and J. Xu, Numerical solution to a mixed Navier- Stokes/Darcy model by the two-grid approach, SIAM J. Numer. Anal., 2009, 47, 3325-3338. doi: 10.1137/080721868 [6] J. Camaño, G. N. Gatica, R. Oyarzúa, R. Ruiz-Baier and P. Venegas, New fully-mixed finite element methods for the Stokes-Darcy coupling, Comput. Methods Appl. Mech. Engrg., 2015, 295, 362-395. doi: 10.1016/j.cma.2015.07.007 [7] P. Chidyagwai and B. Riviere, On the solution of the coupled Navier-Stokes and Darcy equations, Comput. Methods Appl. Mech. Engrg., 2009, 198, 3806-3820. doi: 10.1016/j.cma.2009.08.012 [8] M. Discacciati, E. Miglio and A. Quarteroni, Mathematical and numerical models for coupling surface and groundwater flows, Appl. Numer. Math., 2002, 43, 57-74. doi: 10.1016/S0168-9274(02)00125-3 [9] M. Discacciati, Iterative methods for Stokes/Darcy coupling. In: Domain Decomposition Methods in Science and Engineering, Lect. Notes Comput. Sci. Engrg., Springer, Berlin, 2005, 40, 563-570. [10] G. Z. Du and L. Y. Zuo, Local and parallel finite element method for the mixed Navier-Stokes/Darcy model with Beavers-Joseph interface conditions, Acta Math. Scientia, 2017, 37(5), 1331-1347. doi: 10.1016/S0252-9602(17)30076-0 [11] G. Z. Du, Q. T. Li and Y. H. Zhang, A two-grid method with backtracking for the mixed Navier-Stokes/Darcy model, Numer. Meth. PDEs., 2020, 36(6), 1601-1610. doi: 10.1002/num.22493 [12] G. N. Gatica, R. Oyarzúa and F. J. Sayas, A conforming mixed finite-element method for the coupling of fluid flow with porous media flow, IMA J. Num. Anal., 2009, 29, 86-108. [13] G. N. Gatica, R. Oyarzúa and F. J. Sayas, Analysis of fully-mixed finite element methods for the Stokes-Darcy coupled problem, Math. Comput., 2011, 80, 1911-1948. doi: 10.1090/S0025-5718-2011-02466-X [14] V. Girault and B. Riviere, DG Approximation of coupled Navier-Stokes and Darcy equations by Beaver-Joseph-Saffman interface condition, SIAM J. Numer. Anal., 2009, 47(3), 2052-2089. doi: 10.1137/070686081 [15] X. M. He, J. Li, Y. P. Lin and J. Ming, A domain decomposition method for the steady-state Navier-Stokes-Darcy model with the Beavers-Joseph interface condition, SIAM J. Sci. Comput., 2015, 37, S264-S290. doi: 10.1137/140965776 [16] F. Hecht, FreeFEM++, J. Numer. Math., 2012, 20, 251-265. [17] Y. R. Hou, Optimal error estimates of a decoupled scheme based on two-grid finite element for mixed Stokes-Darcy model, Appl. Math. Letters, 2016, 57, 90-96. doi: 10.1016/j.aml.2016.01.007 [18] Y. R. Hou and S. C. Pei, On the weak solutions to steady Navier-Stokes equations with mixed boundary conditions, Math. Zeit., 2019, 291(1-2), 47-54. doi: 10.1007/s00209-018-2072-7 [19] P. Huang, J. Chen and M. Cai, A mixed and nonconforming FEM with nonmatching meshes for a coupled Stokes-Darcy model, J. Sci. Comput., 2012, 53, 377-394. doi: 10.1007/s10915-012-9574-y [20] W. J. Layton, F. Schieweck and I. Yotov, Coupling fluid flow with porous media flow, SIAM J. Numer. Anal., 2003, 40, 2195-2218. [21] W. J. Layton, Introduction to the Numerical Analysis of Incompressible Viscous Flows, Comput. Sci. Eng. 6, SIAM, Philadelphia, 2008. [22] M. A. A. Mahbub, N. J. Nasu, C. Qiu and H. Zheng, Coupled and decoupled stabilized mixed finite element methods for nonstationary dual-porosity-Stokes fluid flow model, Int. J. Numer. Methods Engrg., 2019, 120(6), 803-833. doi: 10.1002/nme.6158 [23] M. A. A. Mahbub, F. Shi, N. J. Nasu, Y. Wang and H. Zheng, Mixed stabilized finite element method for the stationary Stokes-dual-permeability fluid flow model, Comput. Methods Appl. Mech. Engrg., 2020, 358, 112616. doi: 10.1016/j.cma.2019.112616 [24] M. A. A. Mahbub, X. M. He, N. J. Nasu, C. Qiu, Y. Wang and H. Zheng, A coupled multiphysics model and a decoupled stabilized finite element method for the Closed-Loop geothermal system, SIAM J. Sci. Comput., 2020, 42(4), B951-B982. doi: 10.1137/19M1293533 [25] M. Mu and J. Xu, A two-grid method of a mixed Stokes-Darcy model for coupling fluid flow with porous media flow, SIAM J. Numer. Anal., 2007, 45, 1801-1813. doi: 10.1137/050637820 [26] M. Mu and X. H. Zhu, Decoupled schemes for a non-stationary mixed Stokes-Darcy model, Math. Comput., 2010, 79, 707-731. [27] Y. Qin and Y. R. Hou, Optimal error estimates of a decoupled scheme based on two-grid finite element for mixed Navier-Stokes/Darcy Model, Acta Math. Scientia, 2018, 38B(4), 1361-1369. [28] H. Rui and R. Zhang, A unified stabilized mixed finite element method for coupling Stokes and Darcy flows, Comput. Methods Appl. Mech. Engrg., 2009, 198, 33-36. [29] L. Shan and H. Zheng, Partitioned time stepping method for fully evolutionary Stokes-Darcy flow with Beavers-Joseph interface conditions, SIAM J. Numer. Anal., 2013, 51, 813-839. doi: 10.1137/110828095 [30] L. Shan, H. Zheng and W. J. Layton, A decoupling Method with different subdomain time steps for the nonstationary Stokes-Darcy model, Numer. Methods PDEs, 2013, 29, 549-583. doi: 10.1002/num.21720 [31] S. K. F. Stoter, P. Muller, L. Cicalese, M. Tuveri, D. Schillinger and T. J. R. Hughes, A diffuse interface method for the Navier-Stokes/Darcy equations: Perfusion profile for a patient-specific human liver based on MRI scans, Comput. Meth. Appl. Mech. Engrg., 2017, 321, 70-102. doi: 10.1016/j.cma.2017.04.002 [32] J. P. Yu, M. A. A. Mahbub, F. Shi and H. B. Zheng, Stabilized finite element method for the stationary mixed Stokes-Darcy problem, Adv. Differ. Equ, 2018, 346. [33] J. P. Yu, F. Shi and J. P. Zhao, A stabilized coupled method and its optimal error estimates for elliptic interface problems, Adv. Differ. Equ., 2019, 1, 400. doi: 10.1186/s13662-019-2332-9/fulltext.html [34] J. P. Yu, Y. Z. Sun, F. Shi and H. B. Zheng, Nitsche's type stabilized finite element method for the fully mixed Stokes-Darcy problem with Beavers-Joseph conditions, Appl. Math. Letters, 2020, 106588. [35] J. Yu, H. Zheng, F. Shi and R. Zhao, Two-grid finite element method for the stabilization of mixed Stokes-Darcy model, Disc. Contin. Dyn. Syst. -B, 2019, 24(1), 387. [36] J. Y. Zhang, H. X. Rui and Y. Z. Cao, A partitioned method with different time steps for coupled Stokes and Darcy flows with transport, Int. J. Numer. Anal. Mod., 2019, 16, 463-498. [37] YH Zhang, L Shan and YR Hou, Well-posedness and finite element approximation for the convection model in superposed fluid and porous layers, SIAM J. Numer. Anal., 2020, 58(1), 541-564. doi: 10.1137/19M1241532 [38] L. Zuo and Y. Hou, Numerical analysis for the mixed Navier-Stokes and Darcy problem with the Beavers-Joseph interface condition, Numer. Meth. PDEs, 2015, 31(4), 1009-1030. doi: 10.1002/num.21933 [39] L. Y. Zuo and G. Z. Du, A multi-grid technique for coupling fluid flow with porous media flow, Comput. Math. Appl., 2018, 75(11), 4012-4021. doi: 10.1016/j.camwa.2018.03.010 [40] L. Zuo and G. Du, A parallel two-grid linearized method for the coupled Navier-Stokes-Darcy problem, Numer. Algor., 2018, 77, 151-165. doi: 10.1007/s11075-017-0308-y -
-
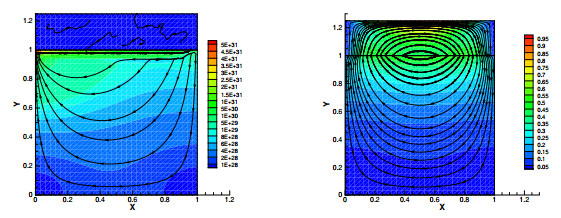
- Figure 1. The streamlines Left, SFEM without stabilization; Right, Stabilized mixed method.
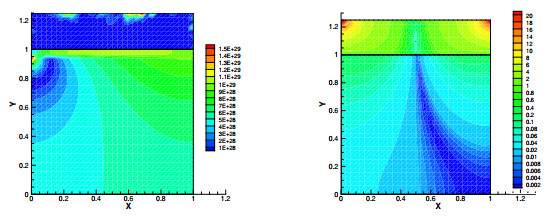
- Figure 2. The pressure contours: Left, SFEM without stabilization; Right, Stabilized mixed method.




 DownLoad:
DownLoad: