| Citation: | Erin Ellefsen, Nancy Rodríguez. ON EQUILIBRIUM SOLUTIONS TO NONLOCAL MECHANISTIC MODELS IN ECOLOGY[J]. Journal of Applied Analysis & Computation, 2021, 11(6): 2664-2686. doi: 10.11948/20200269 |
ON EQUILIBRIUM SOLUTIONS TO NONLOCAL MECHANISTIC MODELS IN ECOLOGY
-
Abstract
Understanding the factors that drive species to move and develop territorial patterns is at the heart of spatial ecology. In many cases, mechanistic models, where the movement of species is based on local information, have been proposed to study such territorial patterns. In this work, we introduce a nonlocal system of reaction-advection-diffusion equations that incorporate the use of nonlocal information to influence the movement of species. One benefit of this model is that groups are able to maintain coherence without having a home-center. As incorporating nonlocal mechanisms comes with analytical and computational costs, we explore the potential of using long-wave approximations of the nonlocal model to determine if they are suitable alternatives that are more computationally efficient. We use the gradient flow-structure of the both local and nonlocal models to compute the equilibrium solutions of the mechanistic models via energy minimizers. Generally, the minimizers of the local models match the minimizers of the nonlocal model reasonably well, but in some cases, the differences in segregation strength between groups is highlighted. In some cases, as we scale the number of groups, we observe an increased savings in computational time when using the local model versus the nonlocal counterpart.
-
Keywords:
- Partial integrodifferential equations /
- population dynamics /
- energy /
- minimizer
-

-
References
[1] A. W. Bateman, M. A. Lewis, G. Gall et al., Territoriality and home-range dynamics in meerkats, Suricata suricatta: A mechanistic modelling approach, Journal of Animal Ecology, 2015, 84(1), 260–271. doi: 10.1111/1365-2656.12267 [2] J. Bedrossian, N. Rodríguez and A. Bertozzi, Local and global well-posedness for aggregation equations and Patlak-Keller-Segel models with degenerate diffusion, Nonlinearity, 2011, 24(6), 1–31. [3] A. Bernoff and C. Topaz, Biological aggregation driven by social and environmental factors: A nonlocal model and its degenerate cahn–hilliard approximation, SIAM Journal on Applied Dynamical Systems, 2015, 15(3), 1528–1562. [4] A. Bertozzi and D. Slepcev, Existence and uniqueness of solutions to an aggregation equation with degenerate diffusion, Communications on Pure and Applied Analysis, 2010, 9(6), 1617–1637. doi: 10.3934/cpaa.2010.9.1617 [5] N. S. Clayton, P. D. Griffiths, N. J. Emery and A. Dickinson, Elements of episodic-like memory in animals., Philosophical Transactions of the Royal Society of London Series B, Biological Sciences, 2001, 356(1972), 1483–1491. [6] J. Clobert, E. Danchin, A. Dhondt and J. D. Nichols, Dispersal, Oxford University Press, Oxford, 2001. [7] M. Heideman, D. Johnson and C. Burrus, Gauss and the history of the fast fourier transform, Archive for History of Exact Sciences, 1985, 34, 265–277. doi: 10.1007/BF00348431 [8] D. Li and X. Zhang, On a nonlocal aggregation model with nonlinear diffusion, Discrete and Continuous Dynamical Systems, 2010, 27(1), 301–323. doi: 10.3934/dcds.2010.27.301 [9] P. K. Molnár, A. E. Derocher, T. Klanjscek and M. A. Lewis, Predicting climate change impacts on polar bear litter size., Nature communications, 2011, 2, 186. doi: 10.1038/ncomms1183 [10] P. Moorcoft, M. A. Lewis and R. Crabree, Home range analysis using a mechanistic home range model, Ecology, 1999, 80(5), 1656–1665. doi: 10.1890/0012-9658(1999)080[1656:HRAUAM]2.0.CO;2 [11] K. Oelschläger, A law of large numbers for moderately interacting diffusion processes, Z. Wahrscheinlichkeitstheorie verw. Gebiete, 1985, 69, 279–322. doi: 10.1007/BF02450284 [12] K. Oelschläger, Large Systems of Interacting Particles and the Porous Medium Equation, Journal of Differential Equations, 1990, 88, 294–346. doi: 10.1016/0022-0396(90)90101-T [13] C. Parmesan and G. Yohe, A globally coherent fingerprint of climate change impacts across natural systems, Nature, 2003, 421(6918), 37–42. doi: 10.1038/nature01286 [14] J. R. Potts and M. A. Lewis, Spatial Memory and Taxis-Driven Pattern Formation in Model Ecosystems, Bulletin of Mathematical Biology, 2019, 81(7), 2725–2747. doi: 10.1007/s11538-019-00626-9 [15] N. Rodríguez and Y. Hu, On the steady-states of a two-species non-local crossdiffusion model, Journal of Applied Analysis, 2020, 26(1), 1–19. doi: 10.1515/jaa-2020-2003 [16] N. Rodríguez and L. Ryzhik, Exploring the effects of social preference, economic disparity, and heterogeneous environments on segregation, Communications in Mathematical Sciences, 2016, 14(2), 363–387. doi: 10.4310/CMS.2016.v14.n2.a3 [17] O. Ronce, How Does It Feel to Be Like a Rolling Stone? Ten Questions About Dispersal Evolution, Annual Review of Ecology, Evolution, and Systematics, 2007, 28, 231–253. [18] E. J. Routh, A Treatise on the Stability of a Given State of Motion, Particularly Steady Motion, London: Macmillan and Co, 1877. [19] N. C. Stenseth, A. Mysterud, G. Ottersen et al., Ecological effects of climate fluctuations, Ecology and climatology, 2002, 297, 1292–1296. [20] L. Wasserstein, Markov processes over denumerable products of spaces describing large systems of automata., Problems of Information Transmission, 1969, 5, 47–52. [21] K. White, M. Lewis and J. Murray, A model for wolf-pack territory formation and maintenance, Journal of Theoretical Biology, 1996, 178, 29–43. doi: 10.1006/jtbi.1996.0004 [22] K. A. J. White, J. D. Murray and M. A. Lewis, Wolf-Deer Interactions: A Mathematical Model, Proceedings of the Royal Society B: Biological Sciences, 1996, 263(1368), 299–305. doi: 10.1098/rspb.1996.0046 [23] S. Zaytseva, J. Shi and L. B. Shaw, Model of pattern formation in marsh ecosystems with nonlocal interactions, Journal of Mathematical Biology, 2020, 80, 655–686. doi: 10.1007/s00285-019-01437-1 -
-
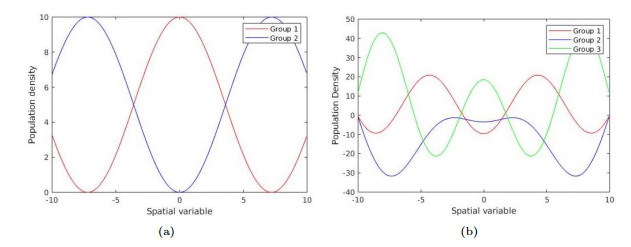
- Figure 1. (a) Analytical solution to (3.5) with two groups interacting (b) The least squares solution to the linear system (3.7) with three groups.
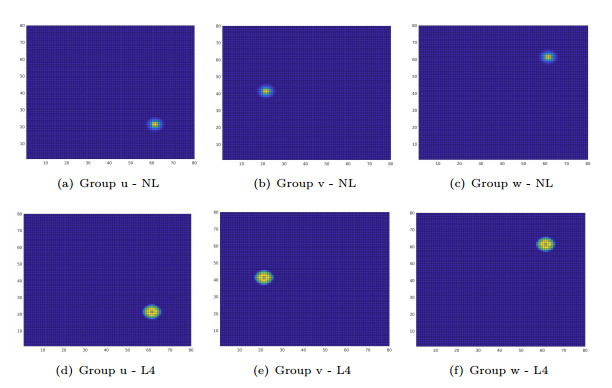
- Figure 2. Energy minimizers for random starting data. NL refers to the non-local model and L4 to the 4th-order approximation.
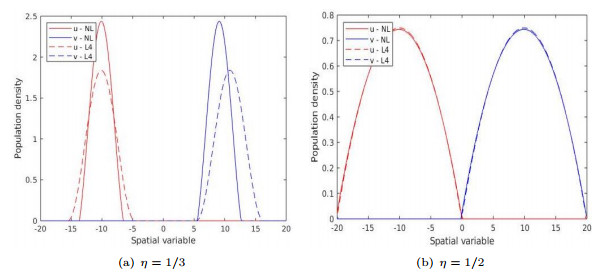
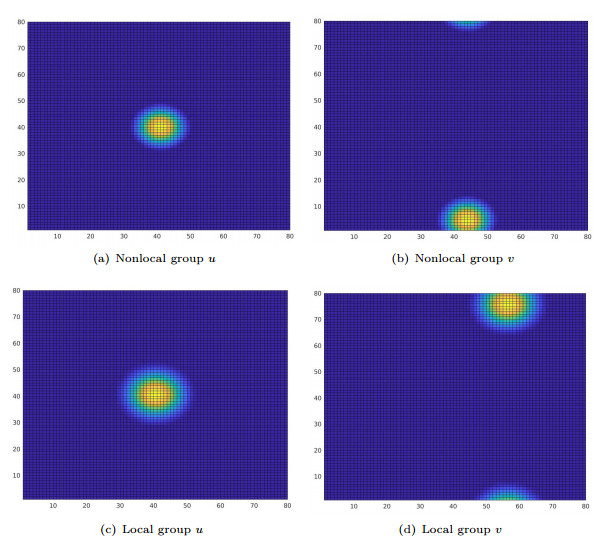
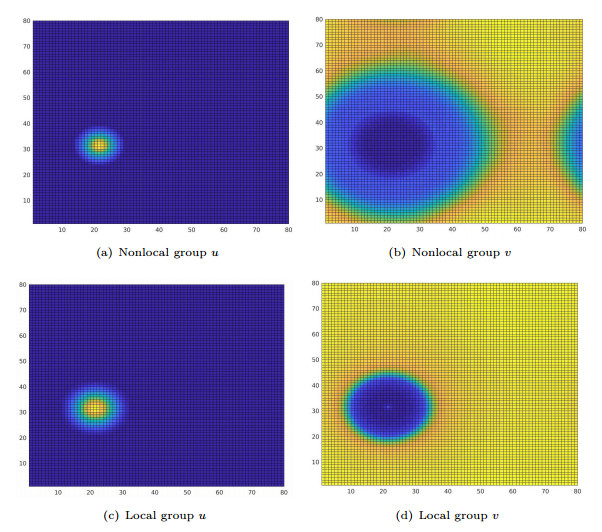
- Figure 3. Energy minimizers for segregated starting data. NL refers to the non-local model, L2 and L4 to the 2nd-order and 4th-order approximations, respectively.
-
Figure 4. Minimizers for random starting data for the nonlocal model with different
$ \eta $ values. - Figure 5. Minimizers for segregated starting data
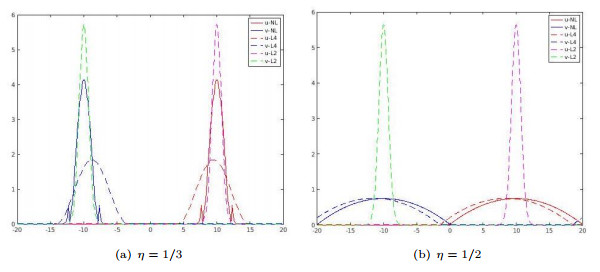
- Figure 6. Minimizers of the nonlocal and the fourth-order approximation energy for random starting data.
-
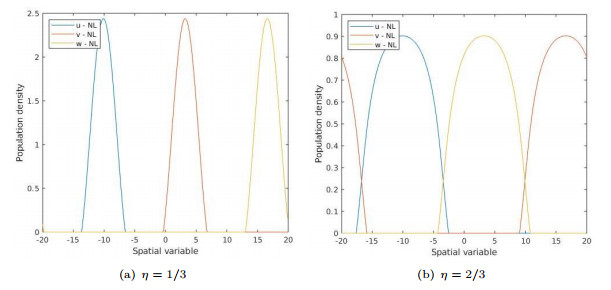
Figure 7. Minimizers of the nonlocal and fourth-order approximation energies with random starting data,
$ \eta = 2/3 $ ,$ a = 2 $ . -
Figure 8. Energy minimizers for the local and nonlocal models with
$ \eta = 1/3 $ . -
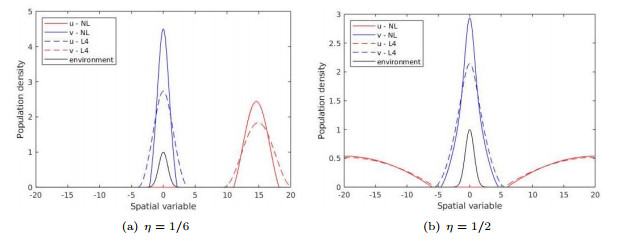
Figure 9. Energy minimizers for the local and nonlocal model with an environment potential with
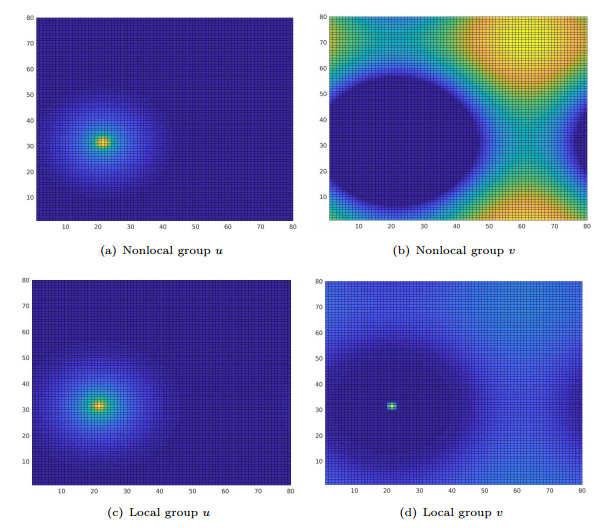
$ \eta = 1/3 $ -
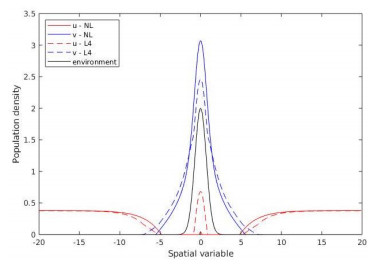
Figure 10. Energy minimizers for the nonlocal model and local approximation with an environment potential,
$ \eta = 1/2 $ -
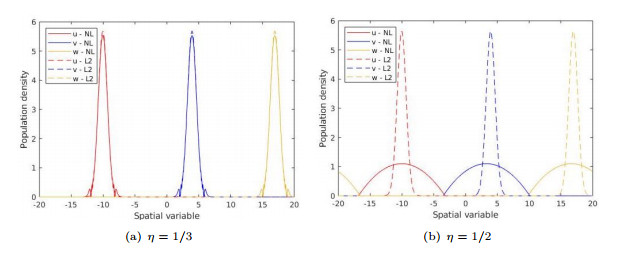
Figure 11. Energy minimizer for three groups with a segregated starting point for both the nonlocal and local model and
$ \eta = 1/3 $ .




 DownLoad:
DownLoad: