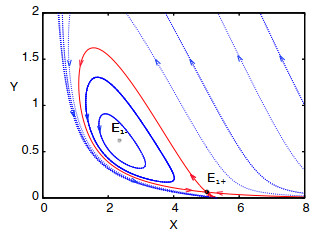
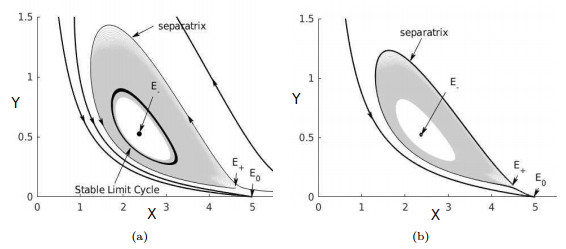
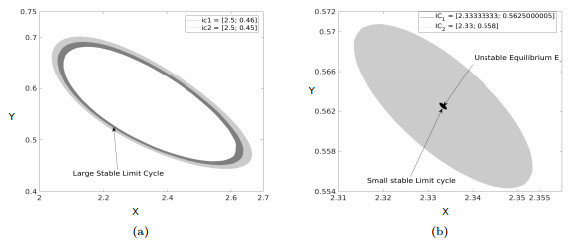
|
[1]
|
S. Altizer, A. Dobson, P. Hosseini, P. Hudson, M. Pascual, P. Rohani, Seasonality and the dynamics of infectious diseases, Ecol. Lett., 2006, 9(4), 467-484. doi: 10.1111/j.1461-0248.2005.00879.x
CrossRef Google Scholar
|
|
[2]
|
R. M. Anderson, R. M. May, B. Anderson, Infectious Diseases of Humans: Dynamics and Control, Oxford University Press Inc, New York, 1992.
Google Scholar
|
|
[3]
|
J. L. Aron, Multiple attractors in the response to a vaccination program, Theor. Popul. Biol., 1990, 38(1), 58-67. doi: 10.1016/0040-5809(90)90003-E
CrossRef Google Scholar
|
|
[4]
|
J. L. Aron, I. B. Schwartz, Seasonality and period-doubling bifurcations in an epidemic model, J. Theor. Biol., 1984, 110(4), 665-679. doi: 10.1016/S0022-5193(84)80150-2
CrossRef Google Scholar
|
|
[5]
|
K. M. Bakker, M. E. Martinez-Bakker, B. Helm, T. J. Stevenson, Digital epidemiology reveals global childhood disease seasonality and the effects of immunization, Proc. National Academy of Sciences, 2016, 113(24), 6689-6694. doi: 10.1073/pnas.1523941113
CrossRef Google Scholar
|
|
[6]
|
M. S. Bartlett, Measles periodicity and community size, J. Royal Statistical Soc., Series A (General), 1957, 120(1), 48-70. doi: 10.2307/2342553
CrossRef Google Scholar
|
|
[7]
|
B. Bolker, B. Grenfell, B. Chaos and biological complexity in measles dynamics, Proc. R. Soc. Lond. B 251, 1993, (1330), 75-81.
Google Scholar
|
|
[8]
|
B. Buonomo, N. Chitnis, A. d'Onofrio, Seasonality in epidemic models: a literature review, Ricerche di Matematica, 2017, 67(1), 1-19.
Google Scholar
|
|
[9]
|
D. J. Earn, P. Rohani, B. M. Bolker, B. T. Grenfell, A simple model for complex dynamical transitions in epidemics, Science, 2000, 287(5453), 667-670. doi: 10.1126/science.287.5453.667
CrossRef Google Scholar
|
|
[10]
|
S. Ellner, B. Bailey, G. Bobashev, A. Gallant, B. Grenfell, D. Nychka, Noise and nonlinearity in measles epidemics: combining mechanistic and statistical approaches to population modeling, AM Naturalist, 1998, 151(5), 425-440. doi: 10.1086/286130
CrossRef Google Scholar
|
|
[11]
|
S. D. Fretwell, Populations in a Seasonal Environment, Princeton University Press, Princeton, 1972.
Google Scholar
|
|
[12]
|
P. Glendinning, L. P. Perry, Melnikov analysis of chaos in a simple epidemiological model, J. Math. Biol., 1997, 35(3), 359-373.
Google Scholar
|
|
[13]
|
N. C. Grassly, C. Fraser, Mathematical models of infectious disease transmission, Nat. Rev. Microbiol., 2008, 6(6), 477-487. doi: 10.1038/nrmicro1845
CrossRef Google Scholar
|
|
[14]
|
B. Grenfell, J. Harwood, (Meta)population dynamics of infectious diseases, Trends Ecol. Evol., 1997, 12(10), 395-399. doi: 10.1016/S0169-5347(97)01174-9
CrossRef Google Scholar
|
|
[15]
|
D. E. Griffin, Immune Responses During Measles Virus Infection, Springer, Berlin, Heidelberg, 1995, 117-134.
Google Scholar
|
|
[16]
|
M. Han, P. Yu, Normal forms, Melnikov functions and bifurcations of limit cycles, Vol. 181, Springer-Verlag, London, 2012.
Google Scholar
|
|
[17]
|
H. W. Hethcote, P. van Den Driessche, Some epidemiological models with nonlinear incidence, J. Math. Biol., 1991, 29(3), 271-287. doi: 10.1007/BF00160539
CrossRef Google Scholar
|
|
[18]
|
S. A. Levin, B. Grenfell, A. Hastings, A. S. Perelson, Mathematical and computational challenges in population biology and ecosystems science, Science, 1997, 275(5298), 334-343. doi: 10.1126/science.275.5298.334
CrossRef Google Scholar
|
|
[19]
|
W. M. Liu, H. W. Hethcote, S. A. Levin, Dynamical behavior of epidemiological models with nonlinear incidence rates, J. Math. Biol., 1987, 25(4), 359-380. doi: 10.1007/BF00277162
CrossRef Google Scholar
|
|
[20]
|
W. M. Liu, S. A. Levin, Y. Iwasa, Influence of nonlinear incidence rates upon the behavior of sirs epidemiological models, J. Math. Biol., 1986, 23(2), 187-204. doi: 10.1007/BF00276956
CrossRef Google Scholar
|
|
[21]
|
W. P. London, J. A. Yorke, Recurrent outbreaks of measles, chickenpox and mumps: I. seasonal variation in contact rates, AM J. Epidemiol., 1973, 98(6), 453-468. doi: 10.1093/oxfordjournals.aje.a121575
CrossRef Google Scholar
|
|
[22]
|
L. F. Olsen, W. M. Schaffer, Chaos versus noisy periodicity: alternative hypotheses for childhood epidemics, Science, 1990, 249(4968), 499-504. doi: 10.1126/science.2382131
CrossRef Google Scholar
|
|
[23]
|
L. F. Olsen, G. L. Truty, W. M. Schaffer, Oscillations and chaos in epidemics: a nonlinear dynamic study of six childhood diseases in Copenhagen, Denmark, Theor. Popul. Biol., 1988, 33(3), 344-370.
Google Scholar
|
|
[24]
|
V. E. Pitzer, C. Viboud, W. J. Alonso, T. Wilcox, C. J. Metcalf, C. A. Steiner, A. K. Haynes, B. T. Grenfell, Environmental drivers of the spatiotemporal dynamics of respiratory syncytial virus in the united states, PLoS Pathogens, 2015, 11(1), e1004591. doi: 10.1371/journal.ppat.1004591
CrossRef Google Scholar
|
|
[25]
|
W. G. Van Panhuis, J. Grefenstette, S. Y. Jung, N. S. Chok, A. Cross, H. Eng, B. Y. Lee, V. Zadorozhny, S. Brown, D. Cummings, D. S. Burke, Contagious diseases in the united states from 1888 to the present, New Engl. J. Med., 2013, 369(22), 2152-2158. doi: 10.1056/NEJMms1215400
CrossRef Google Scholar
|
|
[26]
|
W. M. Schaffer, B. Kendall, C. W. Tidd, L. F. Olsen, Transient periodicity and episodic predictability in biological dynamics, IMA J. Math. Appl. Med. Biol., 1993, 10(4), 227-247. doi: 10.1093/imammb/10.4.227
CrossRef Google Scholar
|
|
[27]
|
D. Schenzle, An age-structured model of pre-and post-vaccination measles transmission, IMA J. Math. Appl. Med. Biol., 1984, 1(2), 169-191. doi: 10.1093/imammb/1.2.169
CrossRef Google Scholar
|
|
[28]
|
I. B. Schwartz, Multiple stable recurrent outbreaks and predictability in seasonally forced nonlinear epidemic models, J. Math. Biol., 1985, 21(3), 347-361. doi: 10.1007/BF00276232
CrossRef Google Scholar
|
|
[29]
|
H. Smith, Subharmonic bifurcation in an sir epidemic model, J. Math. Biol., 1983, 17(2), 163-177. doi: 10.1007/BF00305757
CrossRef Google Scholar
|
|
[30]
|
J. Wingfield, G. Kenagy, Natural Regulation of Reproductive Cycles, In Vertebrate Endocrinology: Fundamentals and Biomedical Implications (Eds. P. K. T. Pang and M. P. Schreibman), Vol. 4, Part B, 181-241, 1991.
Google Scholar
|
|
[31]
|
P. Yu, Computation of normal forms via a perturbation technique, J. Sound and Vib., 1998, 211(1), 19-38. doi: 10.1006/jsvi.1997.1347
CrossRef Google Scholar
|
|
[32]
|
P. Yu, W. Zhang, L. M. Wahl, Dynamical analysis and simulation of a 2-dimensional disease model with convex incidence, Commun. Nonlinear Sci. Numer. Simulat., 2016, 37, 163-192. doi: 10.1016/j.cnsns.2015.12.022
CrossRef Google Scholar
|
|
[33]
|
W. Zhang, L. M. Wahl, P. Yu, Conditions for transient viremia in deterministic in-host models: viral blips need no exogenous trigger, SIAM J. Appl. Math., 2013, 73(2), 853-881. doi: 10.1137/120884535
CrossRef Google Scholar
|
|
[34]
|
W. Zhang, L. M. Wahl, P. Yu, Viral blips may not need a trigger: How transient viremia can arise in deterministic in-host models, SIAM Rev., 2014, 56(1), 127-155. doi: 10.1137/130937421
CrossRef Google Scholar
|




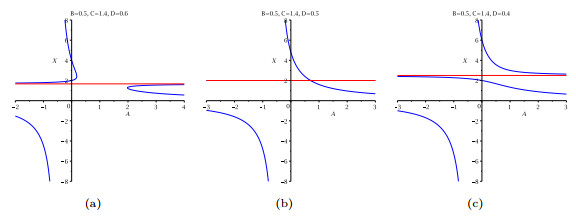

 DownLoad:
DownLoad: