| Citation: | Xiuyan Li, Qiang Ma, Xiaohua Ding. A NOVEL WAY CONSTRUCTING SYMPLECTIC STOCHASTIC PARTITIONED RUNGE-KUTTA METHODS FOR STOCHASTIC HAMILTONIAN SYSTEMS[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 2070-2089. doi: 10.11948/20200315 |
A NOVEL WAY CONSTRUCTING SYMPLECTIC STOCHASTIC PARTITIONED RUNGE-KUTTA METHODS FOR STOCHASTIC HAMILTONIAN SYSTEMS
-
Abstract
In this paper, a novel way of constructing symplectic stochastic partitioned Runge-Kutta methods for stochastic Hamiltonian systems is presented. First, a new class of continuous-stage stochastic partitioned Runge-Kutta methods for partitioned stochastic differential equations are proposed. The order conditions of the continuous-stage stochastic partitioned Runge-Kutta methods are derived via the stochastic B-series theory. The symplectic conditions of the continuous-stage stochastic partitioned Runge-Kutta methods when applied to stochastic Hamiltonian systems are analyzed. Then we prove applying any quadrature formula to a symplectic continuous-stage stochastic partitioned Runge-Kutta method will result in a classical symplectic stochastic partitioned Runge-Kutta method. In this way, various symplectic stochastic partitioned Runge-Kutta methods can be easily constructed by using different quadrature formulas. A concrete symplectic continuous-stage stochastic partitioned Runge-Kutta method of order 1 is constructed and two retrieved stochastic partitioned Runge-Kutta methods are obtained. Numerical experiments are presented to verify the theoretical results and show the effectiveness of the derived methods.
-

-
References
[1] S. Anmarkrud, K. Debrabant and A. Kværnö, General order conditions for stochastic partitioned Runge-Kutta methods, BIT, 2017, 202, 1-24. [2] K. Burrage and P. M. Burrage, High strong order explicit Runge-Kutta methods for stochastic ordinary differential equations, Appl. Numer. Math., 1996, 22(1-3), 81-101. doi: 10.1016/S0168-9274(96)00027-X [3] K. Burrage and P. M. Burrage, Order conditions of stochastic Runge-Kutta methods by B-series, SIAM J. Numer. Anal., 2000, 38(5), 1626-1646. doi: 10.1137/S0036142999363206 [4] J. C. Butcher, Coefficients for the study of Runge-Kutta integration processes, J. Austral. Math. Soc., 1963, 3, 185-201. doi: 10.1017/S1446788700027932 [5] J. C. Butcher, An algebraic theory of integration methods, Math. Comp., 1972, 26, 79-106. doi: 10.1090/S0025-5718-1972-0305608-0 [6] K. Debrabant and A. Kværnö, B-series analysis of stochastic Runge-Kutta methods that use an iterative scheme to compute their internal stage values, SIAM J. Numer. Anal., 2008, 47(1), 181-203. [7] K. Feng and M. Qin, Symplectic Geometric Algorithms for Hamiltonian Systems, Zhejiang Science and Technology Press, Hangzhou, 2003. [8] K. Feng, H. Wu, M. Qin and D. Wang, Construction of canonical difference schemes for Hamiltonian formalism via generating functions, J. Comput. Math., 1989, 7(1), 71-96. [9] S. Gan, Z. Shang and G. Sun, A class of symplectic partitioned Runge-Kutta methods, Appl. Math. Lett., 2013, 26(9), 968-973. doi: 10.1016/j.aml.2013.04.012 [10] E. Hairer, Energy-preserving variant of collocation methods, JNAIAM J. Numer. Anal. Indust. Appl. Math., 2010, 5, 73-84. [11] E. Hairer, C. Lubich and G. Wanner, Geometric Numerical Integration, Springer, Berlin, 2002. [12] M. Han, Q. Ma and X. Ding, High-order stochastic symplectic partitioned Runge-Kutta methods for stochastic Hamiltonian systems with additive noise, Appl. Math. Comput., 2019, 346, 575-593. [13] M. Kamrani and N. Jamshidi, Implicit Milstein method for stochastic differential equations via the Wong-Zakai approximation, Numer. Algor., 2018, 79(2), 357-374. doi: 10.1007/s11075-017-0440-8 [14] P. E. Kloeden and E. Platen, Numerical Solution of Stochastic Differential Equations, Springer, Berlin, 1992. [15] Y. Komori, T. Mitsui and H. Sugiura, Rooted tree analysis of the order conditions of ROW-type scheme for stochastic differential equations, BIT, 1997, 37(1), 43-66. doi: 10.1007/BF02510172 [16] Q. Ma and X. Ding, Stochastic symplectic partitioned Runge-Kutta methods for stochastic Hamiltonian systems with multiplicative noise, Appl. Math. Comput., 2015, 252(2), 520-534. [17] Q. Ma, D. Ding and X. Ding, Symplectic conditions and stochastic generating functions of stochastic Runge-Kutta methods for stochastic Hamiltonian systems with multiplicative noise, Appl. Math. Comput., 2012, 219(2), 635-643. [18] X. Mao, Stochastic Differential Equations and their Applications, Horwood, New York, 1997. [19] G. N. Milstein, Numerical Integration of Stochastic Differential Equations, Kluwer Academic Publishers, Dordrecht, 1995. [20] G. N. Milstein, Y. M. Repin and M. V. Tretyakov, Numerical methods for stochastic systems preserving symplectic structure, SIAM J. Numer. Anal., 2003, 40(4), 1583-1604. [21] T. Misawa, Symplectic integrators to stochastic Hamiltonian dynamical systems derived from composition methods, Math. Probl. Eng., 2010, Article ID: 384937, 12 pages. [22] Y. Miyatake, An energy-preserving exponentially-fitted continuous stage Runge-Kutta method for Hamiltonian systems, BIT Numer. Math., 2014, 54(3), 777-799. doi: 10.1007/s10543-014-0474-4 [23] J. Mujica, Complex Analysis in Banach Spaces, North-Holland, Amsterdam, 1986. [24] K. Nouri, H. Ranjbar and L. Torkzadeh, Modified stochastic theta methods by ODEs solvers for stochastic differential equations, Commun. Nonlinear Sci., 2019, 68, 336-346. doi: 10.1016/j.cnsns.2018.08.013 [25] A. Rößler, Rooted tree analysis for order conditions of stochastic Runge-Kutta methods for the weak approximation of stochastic differential equations, Stoch. Anal. Appl., 2006, 24(1), 97-134. doi: 10.1080/07362990500397699 [26] J. M. Sanz-Serna and M. P. Calvo, Symplectic numerical methods for Hamiltonian problems, Int. J. Mod. Phys. C, 1993, 4(2), 385-392. doi: 10.1142/S0129183193000410 [27] G. Sun, Construction of high order symplectic PRK methods, J. Comput. Math., 1995, 13(1), 40-50. [28] G. Sun, A simple way constructing symplectic Runge-Kutta methods, J. Comput. Math., 2000, 18, 61-68. [29] Y. Tang, J. Cao, X. Liu and Y. Sun, Symplectic methods for the Ablowitz-Ladik discrete nonlinear Schrödinger equation, J. Phys. A-Math. Theor., 2007, 40(10), 2425-2437. doi: 10.1088/1751-8113/40/10/012 [30] W. Tang, G. Lang and X. Luo, Construction of symplectic (partitioned) Runge-Kutta methods with continuous stage, Appl. Math. Comput., 2016, 286, 279-287. [31] W. Tang and Y. Sun, A new approach to construct Runge-Kutta type methods and geometric numerical integrators, AIP. Conf. Proc., 2012, 1479, 1291-1294. [32] L. Wang and J. Hong, Generating functions for stochastic symplectic methods, Discrete Contin. Dyn. Syst., 2014, 34(3), 1211-1228. doi: 10.3934/dcds.2014.34.1211 [33] P. Wang, J. Hong and D. Xu, Construction of symplectic Runge-Kutta methods for stochastic Hamiltonian systems, Commun. Comput. Phys., 2017, 21(1), 237-270. doi: 10.4208/cicp.261014.230616a [34] Y. Wu and B. Wang, Symmetric and symplectic exponential integrators for nonlinear Hamiltonian systems, Appl. Math. Lett., 2019, 90, 215-222. doi: 10.1016/j.aml.2018.11.014 [35] X. Xin, W. Qin and X. Ding, Continuous stage stochastic Runge-Kutta methods, Adv. Differ. Equ., 2021, 2021(1), Article ID: 61, 22 pages. -
-
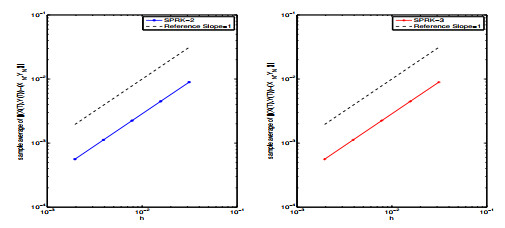
- Figure 1. The convergence rates of SPRK-2 and SPRK-3 for solving (5.1). Left: SPRK-2; Right: SPRK-3
-
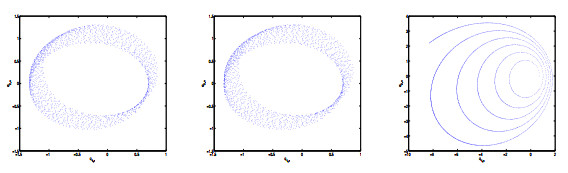
Figure 2. Numerical solutions with respect to
$ (q_{1}, q_{2}) $ of (5.3) computed by the three numerical methods with$ h = 0.1 $ . Left: SPRK-2; Middle: SPRK-3; Right: NS-SPRK -
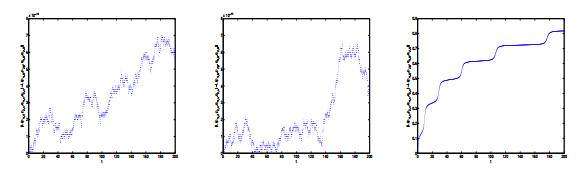
Figure 3. Errors in the angular momentum computed by the three numerical methods for the system (5.3) with
$ h = 0.1 $ . Left: SPRK-2; Middle: SPRK-3; Right: NS-SPRK -
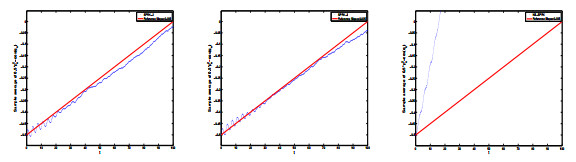
Figure 4. Moments computed by the three numerical methods for the system (5.4) with
$ h = 0.1 $ . Left: SPRK-2; Middle: SPRK-3; Right: NS-SPRK




 DownLoad:
DownLoad: