| Citation: |
Muhammad Ramzan, Yu-Ming Chu, Hamood ur Rehman, Muhammad Shoaib Saleem, Choonkil Park. SOLITON SOLUTIONS FOR ANTI-CUBIC NONLINEARITY USING THREE ANALYTICAL APPROACHES[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 2177-2192. doi: 10.11948/20200380
|
SOLITON SOLUTIONS FOR ANTI-CUBIC NONLINEARITY USING THREE ANALYTICAL APPROACHES
-
Abstract
In this article, three constructive techniques namely, Expa-function method, the modified Kudryashov method and the generalized tanh-method are adopted to analyze the nonlinear Schrödinger equation having anti-cubic nonlinearity. Nonlinear Schrödinger equation is a comprehensive model that governs wave behavior in optical fiber. Cubic-quintic nonlinear Schrödinger equation, additionally having anti-cubic nonlinear term is investigated to construct bright, dark, kink and singular soliton solutions. The graphical representations of the soliton propagation are also demonstrated by the solutions obtained using these three techniques.
-
-
References
[1] M. A. Abdou, The extended tanh method and its applications for solving nonlinear physical models, Appl. Math. Comput., 2007, 190(1), 988-996. [2] A. Akgul and E. Karatas, Reproducing kernel functions for difference equations, Disc. Cont. Dyn. Syst., 2015, 8(6), 1055-1064. [3] A. Akgul, Y. Khan, E. Karatas, D. Baleanu and M. M. Al Qurashi, Solutions of nonlinear systems by reproducing kernel method, J. Nonlinear Sci. Appl., 2017, 10, 4408-4417. doi: 10.22436/jnsa.010.08.33 [4] J. Akter and M. A. Akbar, Exact solutions to the Benney-Luke equation and the Phi-4 equations by using modified simple equation method, Results Phys., 2015, 5, 125-130. doi: 10.1016/j.rinp.2015.01.008 [5] A. T. Ali and E. R. Hassan, General Expa-function method for nonlinear evolution equations, Appl. Math. Comput., 2010, 217(2), 451-459. [6] E. C. Aslan, M. Inc and D. Baleanu, Optical solitons and stability analysis of the NLSE with anti-cubic nonlinearity, Superlattice. Microst., 2017, 109, 784-793. doi: 10.1016/j.spmi.2017.06.003 [7] A. U. Awan, M. Tahir and H. U. Rehman, On traveliing wave solutions: the Wu-Zhang system describing dispersive long waves, Mod. Phys. Lett. B, 2019, 33(6), 1950059. doi: 10.1142/S0217984919500593 [8] A. El Achab, Constructing of exact solutions to the nonlinear Schrödinger equation (NLSE) with power-law nonlinearity by the Weierstrass elliptic function method, Optik, 2016, 127(3), 1229-1232. doi: 10.1016/j.ijleo.2015.10.213 [9] A. Biswas, M. Ekici, A. Sonmezoglu and M. Belic, Chirped and chirp-free optical solitons with generalized anti-cubic nonlinearity by extended trial function scheme, Optik, 2019, 178, 636-644. doi: 10.1016/j.ijleo.2018.09.045 [10] A. Biswas, A. J. M. Jawad, and Q. Zhou, Resonant optical solitons with anti-cubic nonlinearity, Optik, 2018, 157, 525-531. doi: 10.1016/j.ijleo.2017.11.125 [11] A. Biswas, Q. Zhou, S. P. Moshokoa, H. Triki, M. Belic and R. T. Alqahtani, Resonant 1- soliton solution in anti-cubic nonlinear medium with perturbations, Optik, 2017, 145, 14-17. doi: 10.1016/j.ijleo.2017.07.036 [12] A. Biswas, Q. Zhou, M. Z. Ullah, H. Triki, S. P. Moshokoa and M. Belic, Optical soliton perturbation with anti-cubic nonlinearity by semi-inverse variational principle, Optik, 2017, 143, 131-134. doi: 10.1016/j.ijleo.2017.06.087 [13] C. Dai and Y. Wang, Infinite generation of soliton-like solutions for complex nonlinear evolution differential equations via the NLSE based constructive method, Appl. Math. Comput., 2014, 236(1), 606-612. [14] H. S. Eisenberg, Y. Silberberg, R. Morandotti, A. R. Boyd and J. S. Aitchison, Discrete Spatial Optical Solitons in Waveguide Arrays, Phys. Rev. Lett., 1998, 81(16), 33-83. [15] M. Ekici, M. Mirzazadeh, A. Sonmezoglu, M. Z. Ullah, Q. Zhou, H. Triki, S. P. Moshokoa and A. Biswas, Optical solitons with anti-cubic nonlinearity by extended trial equation method, Optik, 2017, 136, 368-373. doi: 10.1016/j.ijleo.2017.02.004 [16] M. Ekici, M. Mirzazadeh, A. Sonmezoglu, Q. Zhou, S. P. Moshokoa, A. Biswas and M. Belic, Dark and singular optical solitons with Kundu-Eckhaus equation by extended trial equation method and extended (G'/G)-expansion scheme, Optik, 2016, 127, 10490-10497. doi: 10.1016/j.ijleo.2016.08.074 [17] M. Eslami, Trial solution technique to chiral nonlinear Schrödinger equation in (1+2)- dimensions, Nonlinear Dyn., 2016, 85, 813-816. doi: 10.1007/s11071-016-2724-2 [18] M. Eslami, M. Mirzazadeh and A. Biswas, Soliton solutions of the resonant nonlinear Schrodinger's equation in optical fibers with time-dependent coefficients by simplest equation approach, J. Mod. Opt., 2013, 60, 1627-1636. doi: 10.1080/09500340.2013.850777 [19] M. Eslami, M. Mirzazadeh and A. Biswas, Optical solitons for the resonant nonlinear Schrodinger's equation with time-dependent coefficients by the first integral method, Optik, 2013, 125, 3107-3116. [20] R. Fedele, H. Schamel, V. I. Karpman and P. K. Shukla, Envelope solitons of nonlinear Schrodinger equation with an anti-cubic nonlinearity, J. Phys. A: Math. Gen., 2003, 36(4), 1169-1173. doi: 10.1088/0305-4470/36/4/322 [21] Y. Guo and Y. Wang, On Weierstrass elliptic function solutions for a (N+1) dimensional potential KdV equation, Appl. Math. Comput., 2011, 217(20), 8080-8092. [22] Q. M. U. Hasan, H. Naher, F. Abdullah and S. T. Mohyud-Din, Solutions of the nonlinear evolution equation via the generalized Riccati equation mapping together with the (G'/G)-expansion method, J. Comput. Anal. Appl., 2016, 21(1), 62-82. [23] K. Hosseini, P. Mayeli and R. Ansari, Modified Kudryashov method for solving the conformable timefractional Klein-Gordon equations with quadratic and cubic nonlinearities, Optik, 2016, 130, 737-742. [24] M. Inc, M. T. Gencoglu and A. Akgul, Application of extended Adomian decomposition method and extended variational iteration method to Hirota-Satsuma coupled kdv equation, J. Adv. Phys., 2017, 6(2), 216-222. doi: 10.1166/jap.2017.1326 [25] M. Inc, B. Kilic, E. Karatas and A. Akgul, Solitary Wave Solutions for the Sawada-Kotera Equation, J. Adv. Phys., 2017, 6(2), 288-293. doi: 10.1166/jap.2017.1318 [26] M. Inc, A. Yusuf, A. Aliyu and D. Baleanu, Dark and singular optical solitons for the conformable space-time nonlinear Schrodinger equation with Kerr and power law nonlinearity, Optik, 2018, 162, 65-75. doi: 10.1016/j.ijleo.2018.02.085 [27] A. Jamaludin, K. Naganthran, R. Nazar and I. Pop, MHD mixed convection stagnation-point flow of Cu-Al2O3/water hybrid nanofluid over a permeable stretching/shrinking surface with heat source/sink, Eur. J. Mech. B Fluids, 2020, 84, 71-80. doi: 10.1016/j.euromechflu.2020.05.017 [28] E. V. Krishnan, A. Biswas, Q. Zhou and M. M. Babatin, Optical solitons with anti-cubic nonlinearity by mapping methods, Optik, 2018, 170, 520-526. doi: 10.1016/j.ijleo.2018.06.010 [29] J. Manafian, Optical soliton solutions for Schrdinger type nonlinear evolution equations by the tan(φ/2)-expansion method, Optik, 2016, 127, 4222-4245. doi: 10.1016/j.ijleo.2016.01.078 [30] M. Matinfar and M. Ghanbari, Homotopy perturbation method for the Fisher's equation and its generalized form, Int. J. Nonlinear Sci., 2009, 8(4), 448-55. [31] M. Mirzazadeh, R. T. Alqahtani and A. Biswas, Optical soliton perturbation with quadratic-cubic nonlinearity by Riccati-Bernoulli sub-ODE method and Kudryashov's scheme, Optik, 2017, 145, 74-78. doi: 10.1016/j.ijleo.2017.07.011 [32] S. T. Mohyud-Din, Y. Khan, N. Faraz and A. Yildirim, Exp-function method for solitary and periodic solutions of Fitzhugh-Nagumo equation, Int. J. Numer. Method H., 2012, 22(3), 335-341. doi: 10.1108/09615531211208042 [33] S. T. Mohyud-Din, E. Negahdary and M. Usman, Emerald Article: A meshless numerical solution of the family of generalized fifth-order Korteweg-de Vries equations, Int. J. Numer. Method H., 2012, 22(5), 641-658. doi: 10.1108/09615531211231280 [34] S. T. Mohyud-Din, M. A. Noor, K. I. Noor and M. M. Hosseini, Variational iteration method for re-formulated partial differential equations, Int. J. Nonlinear Sci. Numer. Simul., 2010, 11(2), 87-92. [35] S. T. Mohyud-Din, A. Yildirim and S. A. Sezer, Numerical soliton solutions of improved Boussinesq equation, Int. J. Numer. Method H., 2011, 21(7), 822-827. doi: 10.1108/09615531111162800 [36] M. A. Noor, S. T. Mohyud-Din, A. Waheed and E. A. Al-Said, Exp-function method for traveling wave solutions of nonlinear evolution equations, Appl. Math. Comput., 2012, 216(2), 477-483. [37] M. S. Osman, A. Korkmaz, H. Rezazadeh, M. Mirzazadeh, M. Eslami and Q. Zhou, The unified method for conformable time fractional Schrodinger equation with perturbation terms, Chin. J. Phys., 2018, 56(5), 2500-2506. doi: 10.1016/j.cjph.2018.06.009 [38] H. Rezazadeh, New solitons solutions of the complex Ginzburg-Landau equation with Kerr law nonlinearity, Optik, 2018, 167, 218-227. doi: 10.1016/j.ijleo.2018.04.026 [39] H. Rezazadeh, S. M. Mirhosseini-Alizamini, M. Eslami, M. Rezazadeh, M. Mirzazadeh and S. Abbagari, New optical solitons of nonlinear conformable fractional Schrodinger-Hirota equation, Optik, 2018, 172, 545-553. doi: 10.1016/j.ijleo.2018.06.111 [40] M. Savescu, A. H. Bhrawy, E. M. Hilal, A. A. Alshaery and A. Biswas, Optical solitons in bire- fringent fibers with four-wave mixing for Kerr law nonlinearity, Rom. J. Phys., 2014, 59, 582-589. [41] M. Tahir and A. U. Awan, Analytical solitons with the Biswas-Milovic equation in the presence of spatio-temporal dispersion in non Kerr-law media, Eur. Phys. J. Plus, 2019, 134(9), 464. doi: 10.1140/epjp/i2019-12887-3 [42] M. Tahir and A. U. Awan, The study of complexitons and periodic solitary-wave solutions with fifth-order KdV equation in (2+1) dimensions, Mod. Phys. Lett. B, 2019, 33(33), 1950411. doi: 10.1142/S0217984919504116 [43] M. Tahir and A. U. Awan, Optical dark and singular solitons to the Biswas-Arshed equation in birefringent fibers without four-wave mixing, Optik, 2020, 207, 164421. doi: 10.1016/j.ijleo.2020.164421 [44] M. Tahir and A. U. Awan, Optical travelling wave solutions for the Biswas-Arshed model in Kerr and non-Kerr law media, Pramana, 2020, 94(1), 1-8. doi: 10.1007/s12043-019-1882-4 [45] M. Tahir and A. U. Awan, Optical singular and dark solitons with Biswas-Arshed model by modified simple equation method, Optik, 2020, 202, 163523. doi: 10.1016/j.ijleo.2019.163523 [46] M. Tahir, A. U. Awan, M. S. Osman, D. Baleanu and M. M. Alqurashi, Abundant periodic wave solutions for fifth-order Sawada-Kotera equations, Results Phys., 2020, 17, 103105. doi: 10.1016/j.rinp.2020.103105 [47] M. Tahir, A. U. Awan and H. U. Rehman, Dark and singular optical solitons to the Biswas-Arshed model with Kerr and power law nonlinearity, Optik, 2019, 185, 777-783. [48] M. Tahir, A. U. Awan and H. U. Rehman, Optical solitons to Kundu-Eckhaus equation in birefringent fibers without four-wave mixing, Optik, 2019, 199, 163297. [49] H. Triki, A. H. Kara, A. Biswas, S. P. Moshokoa and M. Belic, Optical solitons and conservation laws with anti-cubic nonlinearity, Optik, 2016, 127(24), 12056-12062. doi: 10.1016/j.ijleo.2016.09.122 [50] N. Ullah, H. U. Rehman, M. A. Imran and T. Abdeljawad, Highly dispersive optical solitons with cubic law and cubic-quintic-septic law nonlinearities, Results Phys., 2020, 17, 103021. [51] M. Wang, Y. Zhou and Z. Li, Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics, Phys. Lett. A, 1996, 216, 67-75. [52] V. E. Zakharov and A. B. Shabat, Exact Theory of Two-Dimensional Self-Focusing and One-Dimensional Self-Modulation of Waves in Nonlinear Media, Sov. Phys. JETP, 1972, 34(1), 62-69. [53] Z. Zhang, New exact solutions to be generalized nonlinear Schrödinger equation, Fizika A, 2008, 17, 125-134. -
-
Figures(7)
Export File
Citation
Muhammad Ramzan, Yu-Ming Chu, Hamood ur Rehman, Muhammad Shoaib Saleem, Choonkil Park. SOLITON SOLUTIONS FOR ANTI-CUBIC NONLINEARITY USING THREE ANALYTICAL APPROACHES[J]. Journal of Applied Analysis & Computation, 2021, 11(4): 2177-2192. doi: 10.11948/20200380
Format
Content
DownLoad:
-
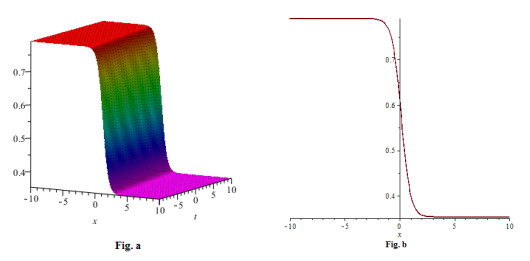
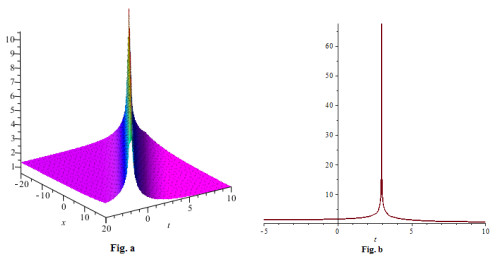
Figure 1. (a) 3-D plot of solution (5.4) for
$ -20\leq x \leq20 $ and$ -5 \leq t\leq10 $ (b) 2-D plot of solution (5.4) for$ x = 0 $ and$ -5 \leq t\leq10 $ -
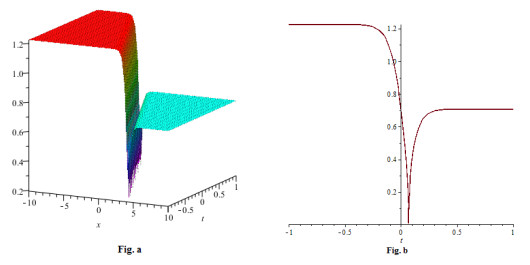
Figure 2. (a) 3-D plot of solution (5.8) for
$ -10\leq x \leq10 $ and$ -10 \leq t\leq10 $ (b) 2-D plot of solution (5.8) for$ -10 \leq x\leq10 $ and$ t = 0 $ -
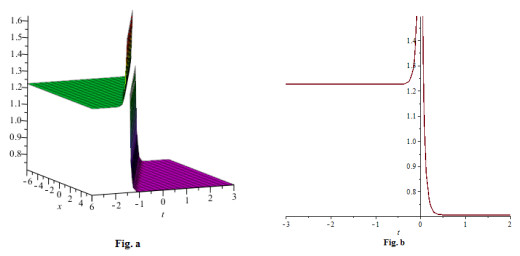
Figure 3. (a) 3-D plot of solution (5.12) for
$ -10\leq x \leq10 $ and$ -1 \leq t\leq1 $ (b) 2-D plot of solution (5.12) for$ x = 0 $ and$ -1\leq t \leq1 $ -
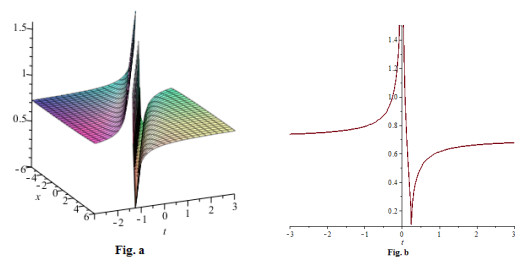
Figure 4. (a) 3-D plot of solution (5.13) for
$ -6\leq x \leq6 $ and$ -3 \leq t\leq3 $ (b) 2-D plot of solution (5.13) for$ x = 0 $ and$ -3\leq t \leq3 $ -
Figure 5. (a) 3D plot of solution (5.14) for
$ -6\leq x \leq6 $ and$ -3 \leq t\leq3 $ (b) 2D plot of solution (5.14) for$ x = 0 $ and$ -3\leq t \leq3 $ -
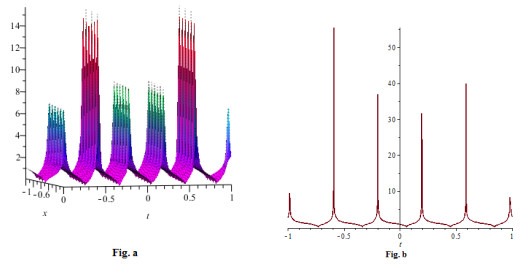
Figure 6. (a) 3D plot of solution (5.15) for
$ -1\leq x \leq0 $ and$ -1 \leq t\leq1 $ (b) 2D plot of solution (5.15) for$ x = 0 $ and$ -1\leq t \leq1 $ -
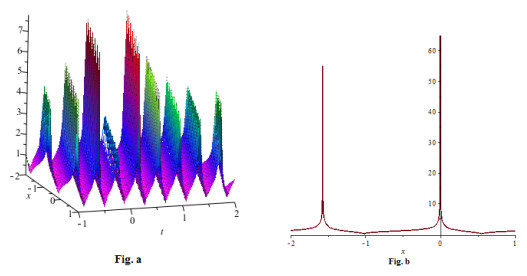
Figure 7. (a) 3D plot of solution (5.16) for
$ -2\leq x \leq1 $ and$ -1 \leq t\leq2 $ (b) 2D plot of solution (5.16) for$ -2\leq x \leq1 $ and$ t = 0 $