| Citation: |
Mardo Gonzales Herrera, César E. Torres Ledesma. NUMERICAL SOLUTION OF THE TIME FRACTIONAL ORDER DIFFUSION EQUATION WITH MIXED BOUNDARY CONDITIONS USING MIMETIC FINITE DIFFERENCE[J]. Journal of Applied Analysis & Computation, 2021, 11(6): 3044-3062. doi: 10.11948/20210115
|
NUMERICAL SOLUTION OF THE TIME FRACTIONAL ORDER DIFFUSION EQUATION WITH MIXED BOUNDARY CONDITIONS USING MIMETIC FINITE DIFFERENCE
-
Abstract
This paper is devoted to the numerical treatment of time fractional diffusion equation with mixed boundary conditions. A new scheme based on the combination of the implicit finite difference method for Caputo derivative in time and the mimetic finite difference in space is derived for solving this problem. The numerical results are provided to demonstrate the effectiveness of the proposed method as compared with other finite difference methods.
-
-
References
[1] A. Arrarás, L. Portero and J. Jorge, Convergence of fractional step mimetic finite difference discretizations for similinear parabolic problems, Applied Numerical Mathematics, 2010, 60, 473-485. doi: 10.1016/j.apnum.2009.10.007 [2] M. Benchohra, A. Cabada and D. Seba, An existence result for nonlinear fractional differential equations on Banach spaces, Bound. Value Probl., 2009, Article ID 628916, 11 pp. [3] R. Brociek, Implicite finite difference method for time fractional heat equation with mixed boundary conditions, Institute of Mathematics silesion University of Technology, 2014, 4. [4] J. Castillo and R. Grone, A Matrix Analysis approach to higher-order approximations for Divergence and gradients satisfying a global conservation law, Society for industrial and applied mathematics, 2003, 5(1), 128-142. [5] J. Castillo and M. Yasuda, Linear system arising for second order mimetic divergence and gradient operators, Journal of Mathematical Modeling and Algorithm, 2005, 4(1), 67082. [6] J. Castillo and G. Miranda, Mimetic discretization metods, 2013 [7] A. Carpinteri and F. Mainardi, Fractal and Fractional Calculus in Continuum Mechanics, Springer, 1997. [8] R. Gorenflo, F. Mainardi, D. Moretti and P. Paradisi, Time fractional diffusion: a discrete random walk approach, Nonlinear Dynam., 2002, 29, 129-143. doi: 10.1023/A:1016547232119 [9] J. Klafter, S. Lim and R. Metzler, Fractional Dynamics, Singapore, 2012. [10] F. Liu, S. Shen, V. Anh and I. Turner, Analysis of a discrete non-Markovian random walk approximation for the time fractional diffusion equation, ANZIAM J., 2005, 46(E), 488-504. [11] Y. Lin and C. Xu, Finite difference/spectral approximations for the time-fractional diffusion equation, Journal of Computational Physics, 2007, 25, 1533-1552. [12] F. Mainardi, Fractional calculus: Some basic problems in continuum and statistical mechanics, In: Carpinteri, A., Mainardi, F. (eds. ) Fractals and Fractional Calculus in Continuum Mechanics, Springer, Wien, 1997. [13] W. Mitkowski, J. Kacprzyk and J. Baranowski, Advances in the Theory and Applications of Non-integer Order Systems, Springer Inter. Publ., Cham, 2013. [14] D. Murio, Implicit finite difference approximation for time fractional diffusion equations, Comput. Math. Appl., 2008, 56, 1138-1145. doi: 10.1016/j.camwa.2008.02.015 [15] I. Podlubny, Fractional Differential Equations. Academic Press, San Diego, 1999. [16] S. Rabsztyn, D. Slota and R. Witula, Gamma and Beta Functions, Gliwice (in Polish), 2012, 1-2. [17] J. Sabatier, O. P. Agrawal and J. Tenreiro Machado, Advances in Fractional Calculus Theoretical Developments and Applications in Physics and Engineering, Springer, Dordrecht, 2007. [18] S. Yuste, Weighted average finite difference methods for fractional diffusion equations, J. Comput. Phys., 2006, 216, 264-274. doi: 10.1016/j.jcp.2005.12.006 -
-
Figures(11) / Tables(1)
Export File
Citation
Mardo Gonzales Herrera, César E. Torres Ledesma. NUMERICAL SOLUTION OF THE TIME FRACTIONAL ORDER DIFFUSION EQUATION WITH MIXED BOUNDARY CONDITIONS USING MIMETIC FINITE DIFFERENCE[J]. Journal of Applied Analysis & Computation, 2021, 11(6): 3044-3062. doi: 10.11948/20210115
Format
Content
DownLoad:
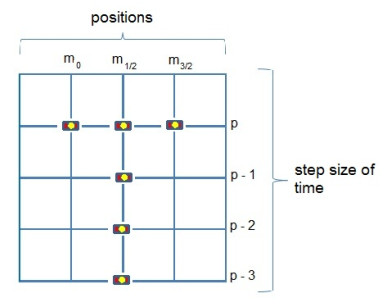
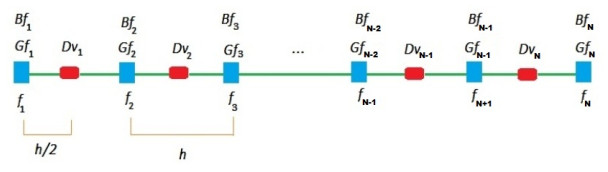
- Figure 1. One-dimensional Uniform Staggered Mesh
- Figure 2. Mesh for the Fractional Order Derivative
-
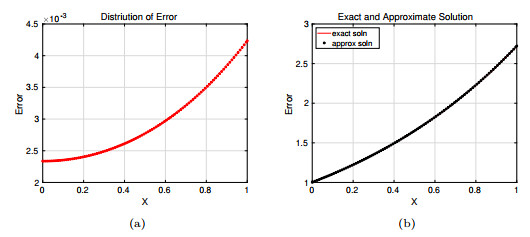
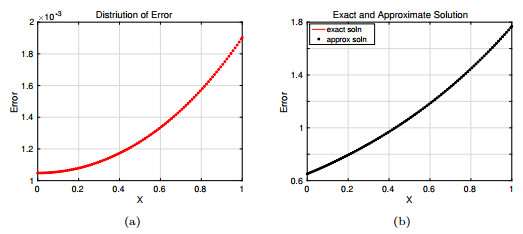
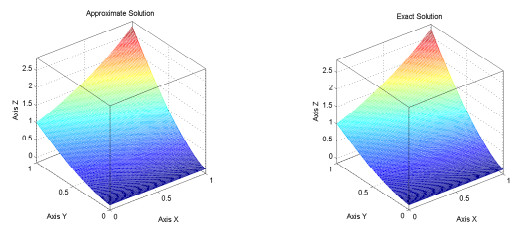
Figure 3. Approximation error obtained with M.F.D method with grid size
$ 1/100 \times 1/100, \; {\rm{at\;time}}\; \; t = 1 $ (a) Distribution of error, (b) comparison of exact and approximate solution. -
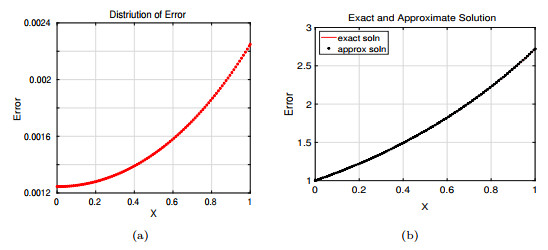
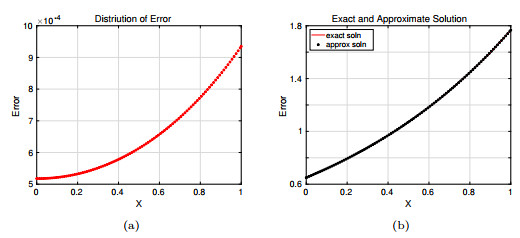
Figure 4. Approximation error obtained with M.F.D method with grid size
$ 1/100 \times 1/200, {\rm{at\;time}}\; t =1 $ (a) Distribution of error, (b) comparison of exact and approximate solution. -
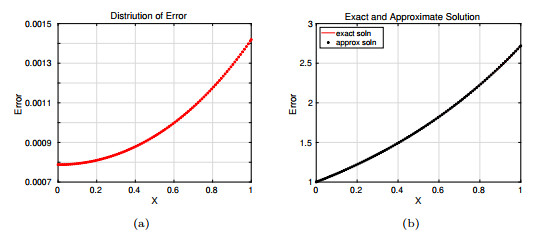
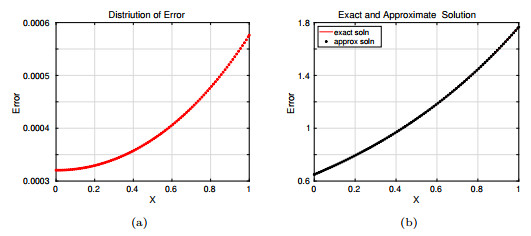
Figure 5. Approximation error obtained with M.F.D method with grid size
$ 1/100 \times 1/300, {\rm{at\;time}}\; t =1 $ (a) Distribution of error, (b) comparison of exact and approximate solution. -
Figure 6. Approximation error obtained with M.F.D method with grid size
$ 1/100 \times 1/100, {\rm{at\;time}}\; t = 0.75 $ (a) Distribution of error, (b) comparison of exact and approximate solution. -
Figure 7. Approximation error obtained with M.F.D method with grid size
$ 1/100 \times 1/200, {\rm{at\;time}}\; t =0.75 $ (a) Distribution of error, (b) comparison of exact and approximate solution. -
Figure 8. Approximation error obtained with M.F.D method with grid size
$ 1/100 \times 1/300, {\rm{at\;time}}\; t = 0.75 $ (a) Distribution of error, (b) comparison of exact and approximate solution. -
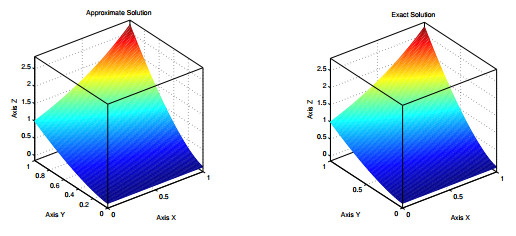
Figure 9. Approximated and exact solutions for a mesh
$ n=m=100 $ -
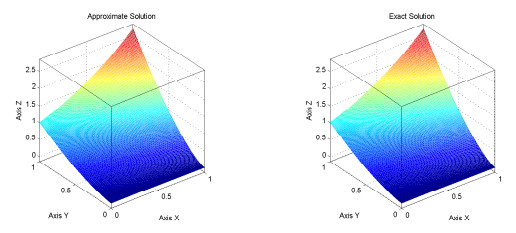
Figure 10. Exact and approximation solution for a mesh
$ n=m=200 $ -
Figure 11. Exact and approximation solution for a mesh
$ n=m=300 $