| Citation: |
Ashish, Jinde Cao, Fawaz Alsaadi. CHAOTIC EVOLUTION OF DIFFERENCE EQUATIONS IN MANN ORBIT[J]. Journal of Applied Analysis & Computation, 2021, 11(6): 3063-3082. doi: 10.11948/20210164
|
CHAOTIC EVOLUTION OF DIFFERENCE EQUATIONS IN MANN ORBIT
-
Abstract
Because of the tremendous characteristics of discrete chaos and sensitivity to their initial parameters, discrete one-dimensional maps are extensively used in every branch of science and engineering such as a security system, cryptography and traffic control models. In this article, it is proposed to examine the chaotic characteristics of a logistic-type difference equation using Mann orbit. Due to the presence of an added parameter α the resulting orbit provides superior chaotic characteristics from those of the existing characteristics in chaotic maps. As compared to existing chaotic maps it provides more efficient and effective chaotic characteristics like better sensitivity, suitable maximum Lyapunov exponent value and superior stability behavior. The results are carried out mathematically as well as experimentally followed by theorems, a few counterexamples and some concluding remarks. Moreover, a superior discrete traffic flow model using macroscopic approach and Greenshield's model is also described.
-
Keywords:
- Chaos /
- period-doubling /
- Lyapunov exponent /
- difference maps
-
-
References
[1] K. T. Alligood, T. D. Sauer and J. A. Yorke, Chaos: An Introduction to Dynamical Systems, Springer Verlag, New York Inc., 1996. [2] M. Andrecut, Logistic map as a random number generator, Int. J. Mod. Phys. B, 1998, 12(921). [3] Ashish, J. Cao and R. Chugh, Chaotic behavior of logistic map in superior orbit and an improved chaos-based traffic control model, Nonlinear Dyn., 2018, 94(2), 959-975. doi: 10.1007/s11071-018-4403-y [4] Ashish and J. Cao, A novel fixed point feedback approach studying the dynamcial behaviour of standard logistic map, Int. J. Bifurc. Chaos, 2019, 29(1), Article ID 1950010, 16 pages. [5] Ashish, J. Cao and R. Chugh, Controlling chaos using superior feedback technique with applications in discrete traffic models, Int. J. Fuzzy Syst., 2019, 21(5), 1467-1479. doi: 10.1007/s40815-019-00636-8 [6] Ashish, J. Cao and R. Chugh, Discrete chaotification in modulated logistic system, Int. J. Bifurc. Chaos, 2021, 31(5), Article ID 2150065, 14 Pages. [7] Ashish, J. Cao, F. Alsaadi and A. K. Malik, Discrete Superior Hyperbolicity in Chaotic Maps, Chaos Theory and Applications, 2021, 3(1), 34-42. doi: 10.51537/chaos.936679 [8] M. Ausloos and M. Dirickx, The Logistic Map and the Route to Chaos: from the Beginnings to Modern Applications, Springer Verlag, New York Inc., 2006. [9] M. S. Baptista, Cryptography with chaos, Physics Letters A, 1998, 240, 50-54. doi: 10.1016/S0375-9601(98)00086-3 [10] A. R. Chowdhary and M. Debnath, Periodicity and Chaos in Modulated Logistic map, Int. J. Theor. Phy., 1990, 29(7), 779-788. doi: 10.1007/BF00673913 [11] R. M. Crownover, Introduction to Fractals and Chaos, Jones and Barlett Publishers, Burlington, 1995. [12] R. L. Devaney, An Introduction to Chaotic Dynamical Systems, 2nd Edition, Addison-Wesley, 1948. [13] R. L. Devaney, A First Course in Chaotic Dynamical Systems: Theory and Experiment, Addison-Wesley, 1992. [14] P. Diamond, Chaotic behaviour of systems of difference equations, Int. J. Systems Sci., 1976, 7(8), 953-956. doi: 10.1080/00207727608941979 [15] L. P. L. de Oliveira and M. Sobottka, Cryptography with chaotic mixing, Chaos Solitons Fractals, 2008, 35(3), 466-471. doi: 10.1016/j.chaos.2006.05.049 [16] S. Effah-Poku, W. Obeng-Denteh and I. K. Dontwi, A Study of Chaos in Dynamical Systems, J. Math., 2008, Article ID 1808953, 5 pages. [17] M. J. Feigenbaum, Quantitative universality for a class of nonlinear transformations, J. Stat. Phys., 1978, 19(1), 25-52. doi: 10.1007/BF01020332 [18] R. A. Holmgren, A First Course in Discrete Dynamical Systems, Springer Verlag, New York Inc., 1994. [19] Khamosh, V. Kumar and Ashish, A Noval Feedback Control System to Study the Stability in Stationary States, J. Math. Comput. Sci., 2020, 10(5), 2094-2109. [20] V. Kumar, Khamosh and Ashish, An Empirical Approach to Study the Stability of Generalized Logistic Map in Superior Orbit, Adv. Math., Sci. J., 2020, 9(10), 8365-8374. [21] K. Li and Z. Gao, Nonlinear dynamics analysis of traffic time series, Mod. Phys. Lett. B, 2004, 18, 1395-1402. doi: 10.1142/S0217984904007943 [22] T. Li and J. A. Yorke, Period Three Implies Chaos, American Mathematical Monthly, 1975, 82(10), 985-992. doi: 10.1080/00029890.1975.11994008 [23] S. C. Lo and H. J. Cho, Chaos and control of discrete dynamic traffic model, J. Franklin Inst., 2005, 342, 839-851. doi: 10.1016/j.jfranklin.2005.06.002 [24] E. N. Lorenz, Deterministic nonperiodic flows, J. Atmos. Sci., 1963, 20, 130-141. doi: 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 [25] W. R. Mann, Mean value methods in iteration, Proc. Amer. Math. Soc., 1953, 4, 506-510. doi: 10.1090/S0002-9939-1953-0054846-3 [26] M. Martelli, Chaos: An Introduction to Discrete Dynamical Systems and Chaos, Wiley-Interscience Publication, New York Inc., 1999. [27] R. May, Simple mathematical models with very complicated dynamics, Nature, 1976, 261, 459-475. doi: 10.1038/261459a0 [28] H. Poincare, Les Methods Nouvells de la Mecanique Leleste, Gauthier Villars, Paris, 1899. [29] A. G. Radwan, On some generalized discrete logistic maps, J. Adv. Res., 2013, 4, 163-171. doi: 10.1016/j.jare.2012.05.003 [30] W. S. Sayed, A. G. Radwan and H. A. H. Fahmy, Design of positive, negative and alternating sign generalized logistic maps, Discrete Dyn. Nat. Soc., 2015, Article ID 586783, 23 pages. [31] P. Shang, X. Li and S. Kame, Chaotic analysis of traffic time series, Chaos Solitons Fractals, 2005, 25, 121-128. doi: 10.1016/j.chaos.2004.09.104 [32] A. N. Sharkovsky, Y. L. Maistrenko and E. Y. Romanenko, Difference Equations and Their Applications, Kluwer Academic Publisher, 1993. [33] N. Singh and A. Sinha, Chaos-based secure communication system using logistic map, Opt. Lasers Eng., 2010, 48, 398-404. doi: 10.1016/j.optlaseng.2009.10.001 [34] N. Smaoui and A. Kanso, Cryptography with chaos and shadowing, Chaos Solitons Fractals, 2009, 42, 2312-2321. doi: 10.1016/j.chaos.2009.03.128 [35] S. H. Strogatz, Nonlinear Dynamics and Chaos, Persus Books Publishing, New York, 1994. [36] M. Xu and Z. Gao, Nonlinear analysis of road traffic flows in discrete dynamical system, J. Comput. Nonlin. Dyn., 2008, 3(2), Article ID 021206, 6 pages. [37] G. Wu and D. Baleanu, Discrete fractional logistic map and its chaos, Nonlinear Dyn., 2014, 75, 283-286. doi: 10.1007/s11071-013-1065-7 [38] G. Wu and D. Baleanu, Discrete chaos in fractional delayed logistic map, Nonlinear Dyn., 2015, 80, 1697-1703. doi: 10.1007/s11071-014-1250-3 -
-
Figures(6) / Tables(1)
Export File
Citation
Ashish, Jinde Cao, Fawaz Alsaadi. CHAOTIC EVOLUTION OF DIFFERENCE EQUATIONS IN MANN ORBIT[J]. Journal of Applied Analysis & Computation, 2021, 11(6): 3063-3082. doi: 10.11948/20210164
Format
Content
DownLoad:
-
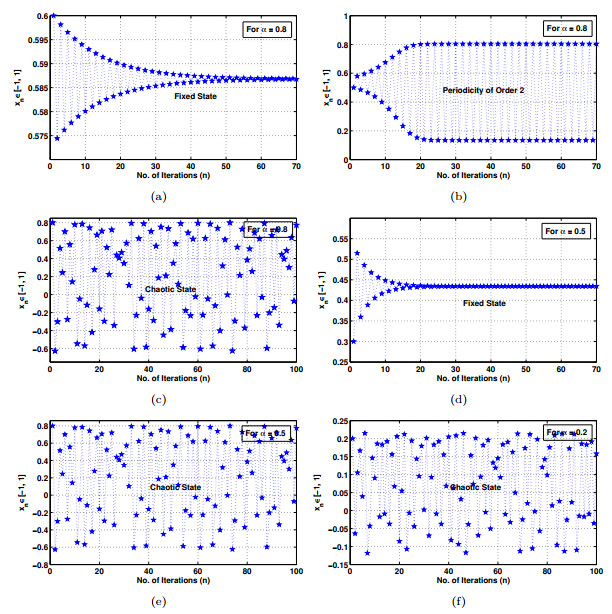
Figure 1. (a) Fixed state plot for the system
$ S(\alpha, \mu, x) $ for$ \mu = 1.2 $ , (b) Periodic state plot for the system$ S(\alpha, \mu, x) $ for$ \mu = 1.5 $ , (c) Chaotic state plot for the system$ S(\alpha, \mu, x) $ for$ \mu = 3 $ , (d) Fixed state plot for the system$ S(\alpha, \mu, x) $ for$ \mu = 3.5 $ , (e) Chaotic state plot for the system$ S(\alpha, \mu, x) $ for$ \mu = 8.5 $ and (f) Chaotic state plot for the system$ S(\alpha, \mu, x) $ for$ \mu = 45 $ -
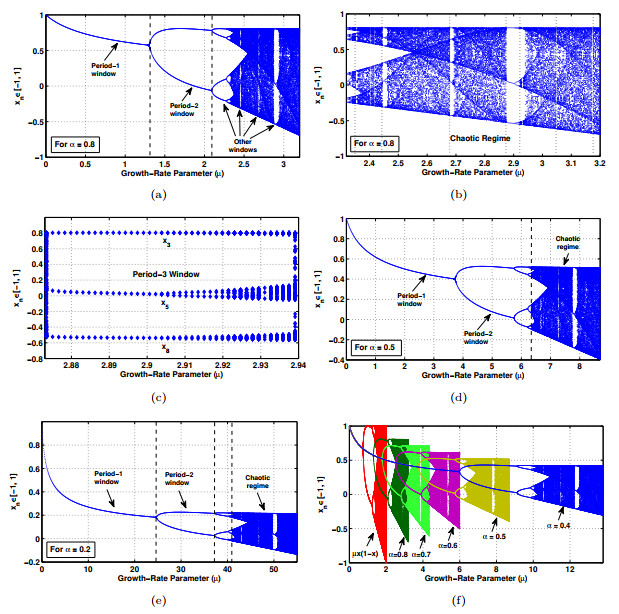
Figure 2. (a) Periodic plot for the system
$ S(\alpha, \mu, x) $ for$ 0\leq\mu \leq3.2 $ , (b) Chaotic regime for the system$ S(\alpha, \mu, x) $ for$ 2.32<\mu \leq3.2 $ , (c) Period three plot for the system$ S(\alpha, \mu, x) $ for$ 2.87\leq\mu \leq2.92 $ , (d) Periodic plot for the system$ S(\alpha, \mu, x) $ for$ 0\leq\mu \leq8.7 $ , (e) Periodic plot for the system$ S(\alpha, \mu, x) $ for$ 0\leq\mu \leq55 $ and (f) Comparative plot for the system$ S(\alpha, \mu, x) $ versus logistic map -
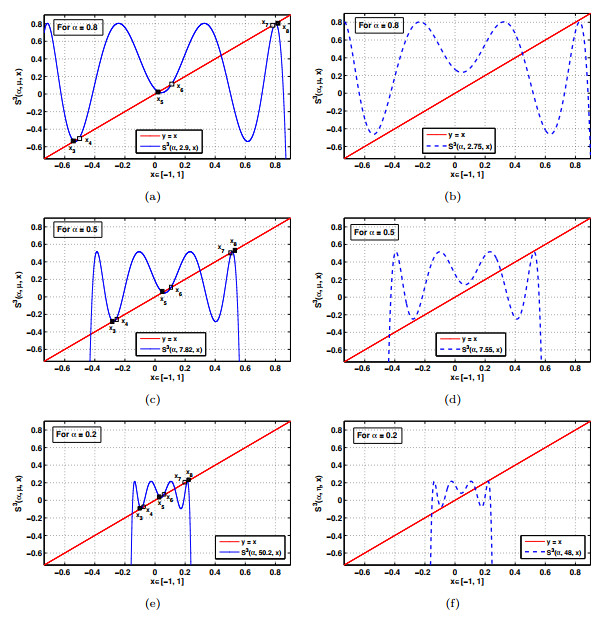
Figure 3. Functional plot for
$ S^3(\alpha, \mu, x) $ (a) when$ \mu = 2.9 $ , (b) when$ \mu = 2.75 $ , (c) when$ \mu = 7.82 $ , (d) when$ \mu = 7.55 $ , (e) when$ \mu = 50.2 $ and (f) when$ \mu = 48 $ -
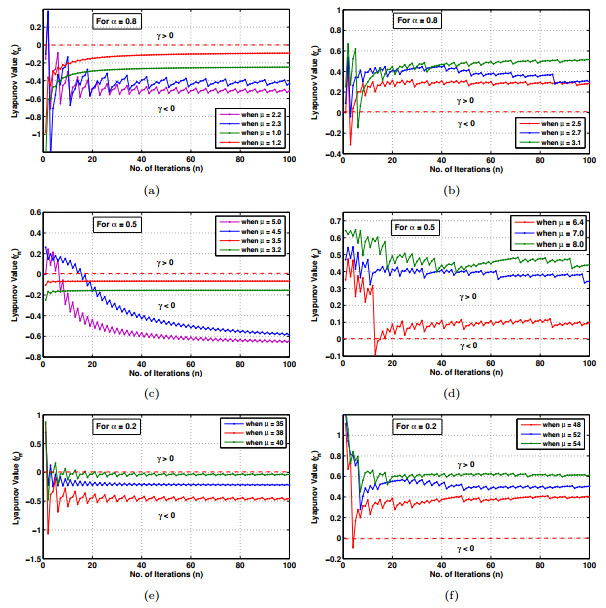
Figure 4. Lyapunov
$ \gamma $ plot for the orbit$ \{S^n(\alpha, \mu, x_0)\} $ (a) when$ \alpha = 0.8 $ and$ 0\leq\mu\leq2.32 $ , (b) when$ \alpha = 0.8 $ and$ 2.32<\mu \leq 3.2 $ , (c) when$ \alpha = 0.5 $ and$ 0\leq\mu\leq6.34 $ , (d) when$ \alpha = 0.5 $ and$ 6.34<\mu \leq 8.7 $ , (e) when$ \alpha = 0.2 $ and$ 0\leq\mu\leq41 $ and (f) when$ \alpha = 0.2 $ and$ 41<\mu \leq 55 $ -
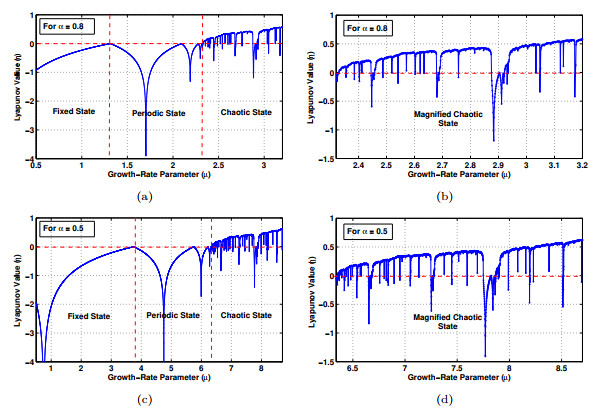
Figure 5. Lyapunov exponent
$ \eta $ plot for the system$ S(\alpha, \mu, x) $ (a) when$ \alpha = 0.8 $ and$ 0\leq \mu \leq3.2 $ , (b) when$ \alpha = 0.8 $ and$ 2.32\leq \mu \leq3.2 $ , (c) when$ \alpha = 0.5 $ and$ 0\leq \mu \leq8.7 $ , and (d) when$ \alpha = 0.5 $ and$ 6.34\leq \mu \leq8.7 $ -
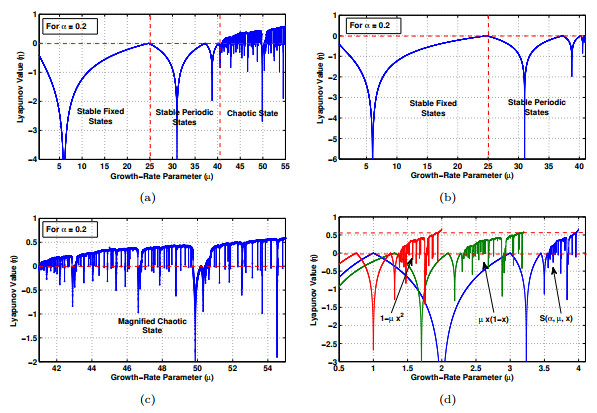
Figure 6. Lyapunov exponent
$ \eta $ plot for the system$ S(\alpha, \mu, x) $ (a) when$ \alpha = 0.2 $ and$ 0\leq \mu \leq55 $ , (b) when$ \alpha = 0.2 $ and$ 0\leq \mu\leq41 $ , (c) when$ \alpha = 0.2 $ and$ 41<\mu\leq55 $ , and (d) versus$ \mu x(1-x) $ and$ 1-\mu x^2 $