| Citation: | Minrong Ren, Yuqian Zhou, Qian Liu. TRAVELING WAVE SOLUTIONS OF THE GENERALIZED (2+1)-DIMENSIONAL KUNDU-MUKHERJEE-NASKAR EQUATION[J]. Journal of Applied Analysis & Computation, 2021, 11(6): 3083-3114. doi: 10.11948/20210192 |
TRAVELING WAVE SOLUTIONS OF THE GENERALIZED (2+1)-DIMENSIONAL KUNDU-MUKHERJEE-NASKAR EQUATION
-
Abstract
In this paper, we consider two types of traveling wave systems of the generalized Kundu-Mukherjee-Naskar equation. Firstly, due to the integrity, we obtain their energy functions. Then, the dynamical system method is applied to study bifurcation behaviours of the two types of traveling wave systems to obtain corresponding global phase portraits in different parameter bifurcation sets. According to them, every bounded and unbounded orbits can be identified clearly and investigated carefully which correspond to various traveling wave solutions of the generalized Kundu-Mukherjee-Naskar equation exactly. Finally, by integrating along these orbits and calculating some complicated elliptic integral, we obtain all type Ⅰ and type Ⅱ traveling wave solutions of the generalized Kundu-Mukherjee-Naskar equation without loss.
-
Keywords:
- GKMN equation /
- traveling wave solution /
- bifurcation /
- dynamical system
-

-
References
[1] A. Biswas, Y. Yıldırım, E. Yaşar, Q. Zhou, S. P. Moshokoa and M. Belic, Optical soliton perturbation with quadratic-cubic nonlinearity using a couple of strategic algorithms, Chin. J. Phys., 2018, 56(5), 1990-1998. doi: 10.1016/j.cjph.2018.09.009 [2] S. N. Chow and J. K. Hale, Methods of bifurcation theory, Springer Science & Business Media, 2012. [3] M. Ekici, A. Sonmezoglu, A. Biswas and M. R. Belic, Optical solitons in (2+1)-dimensions with Kundu-Mukherjee-Naskar equation by extended trial function scheme, Chin. J. Phys., 2019, 57, 72-77. doi: 10.1016/j.cjph.2018.12.011 [4] B. Ghanbari, H. Günerhan, O. A. İlhan and H. M. Baskonus, Some new families of exact solutions to a new extension of nonlinear Schrödinger equation, Phys. Scripta., 2020, 95(7), Article ID: 075208. [5] J. Guckenheimer and P. Holmes, Nonlinear Oscillations, Dynamical Systems and Bifurcation of Vector Fields, Springer, New York, 1983. [6] A. Jhangeer, A. R. Seadawy, F. Ali and A. Ahmed, New complex waves of perturbed Schrödinger equation with Kerr law nonlinearity and Kundu-Mukherjee-Naskar equation, Results Phys., 2020, 16, Article ID: 102816. [7] N. A. Kudryashov, General solution of traveling wave reduction for the Kundu-Mukherjee-Naskar model, Optik., 2019, 186, 22-27. doi: 10.1016/j.ijleo.2019.04.072 [8] A. Kundu, Novel hierarchies & hidden dimensions in integrable field models: theory & application, Journal of Physics: Conference Series, 2014, 482, Article ID: 012022. [9] A. Kundu and A. Mukherjee, Novel integrable higher-dimensional nonlinear Schrödinger equation: properties, solutions, applications, 2013, arXiv: 1305.4023. [10] A. Kundu, A. Mukherjee and T. Naskar, Modelling rogue waves through exact dynamical lump soliton controlled by ocean currents, Proc. R. Soc. Lond. Ser. A Math. Phys., 2014, 470(2164), Article ID: 20130576. [11] D. Kumar, G. C. Paul, T. Biswas, A. R. Seadawy, R. Baowali, M. Kamal and H. Rezazadeh, Optical solutions to the Kundu-Mukherjee-Naskar equation: mathematical and graphical analysis with oblique wave propagation, Phys. Scripta., 2020, 96(2), Article ID: 025218. [12] A. Mukherjee, M. Janaki and A. Kundu, A new (2+1) dimensional integrable evolution equation for an ion acoustic wave in a magnetized plasma, Phys. Plasmas., 2015, 22(7), Article ID: 072302. [13] W. Peng, S. Tian and T. Zhang, Optical solitons, complexitons and power series solutions of a (2+1)-dimensional nonlinear Schrödinger equation, Modern Phys. Lett. B., 2018, 32(28), Article ID: 1850336. [14] D. Qiu, Y. Zhang and J. He, The rogue wave solutions of a new (2+1)-dimensional equation, Commun. Nonlinear Sci. Numer. Simul., 2016, 30(1-3), 307-315. doi: 10.1016/j.cnsns.2015.06.025 [15] S. T. R. Rizvi, I. Afzal and K. Ali, Dark and singular optical solitons for Kundu-Mukherjee-Naskar model, Modern Phys. Lett. B., 2020, 34(6), Article ID: 2050074. [16] H. Rezazadeh, A. Kurt, A. Tozar, O. Tasbozan and S. Mirhosseini-Alizamini, Wave behaviors of Kundu-Mukherjee-Naskar model arising in optical fiber communication systems with complex structure, Opt. Quant. Electon., 2021. DOI: 10.21203/rs.3.rs-168692/v1. [17] S. Singh, A. Mukherjee, K. Sakkaravarthi and K. Murugesan, Higher dimensional localized and periodic wave dynamics in an integrable (2+1)-dimensional deep water oceanic wave model, Wave. Random. Complex., 2021, 1-20. DOI: 10.1080/17455030.2021.1874621. [18] T. A. Sulaiman and H. Bulut, The new extended rational SGEEM for construction of optical solitons to the (2+1)-dimensional Kundu-Mukherjee-Naskar model, Appl. Math. Nonlinear Sci., 2019, 4(2), 513-521. doi: 10.2478/AMNS.2019.2.00048 [19] R. Talarposhti, P. Jalili, H. Rezazadeh, B. Jalili, D. Ganji, W. Adel and A. Bekir, Optical soliton solutions to the (2+1)-dimensional Kundu-Mukherjee-Naskar equation, Internat. J. Modern Phys. B., 2020, 34(11), Article ID: 2050102. [20] X. Wen, Higher-order rational solutions for the (2+1)-dimensional KMN equation, Proc. Rom. Acad. Ser. A Math. Phys., 2017, 18(3), 191-198. [21] Y. Yıldırım, Optical soltons to Kundu-Mukherjee-Naskar model with trial equation approach, Optik., 2019, 183, 1061-1065. doi: 10.1016/j.ijleo.2019.02.117 [22] Y. Yıldırım, Optical soltons to Kundu-Mukherjee-Naskar model with modified simple equation approach, Optik., 2019, 184, 247-252. doi: 10.1016/j.ijleo.2019.02.135 [23] Y. Yıldırım, Optical soltons to Kundu-Mukherjee-Naskar model in birefringent fibers with trial equation approach, Optik., 2019, 183, 1026-1031. doi: 10.1016/j.ijleo.2019.02.141 [24] Y. Yıldırım, Optical solitons to Kundu-Mukherjee-Naskar model in birefringent fibers with modified equation approach, Optik., 2019, 184, 121-127. doi: 10.1016/j.ijleo.2019.02.155 [25] Y. Yıldırım and M. Mirzazadeh, Optical pulses with Kundu-Mukherjee-Naskar model in fiber communication systems, Chinese J. Phys., 2020, 64, 183-193. doi: 10.1016/j.cjph.2019.10.025 [26] Z. Zhang, T. Ding, W. Huang and Z. Dong, Qualitative Theory of Differential Equations, American Mathematical Society, Providence, RI, USA, 1992. -
-
-
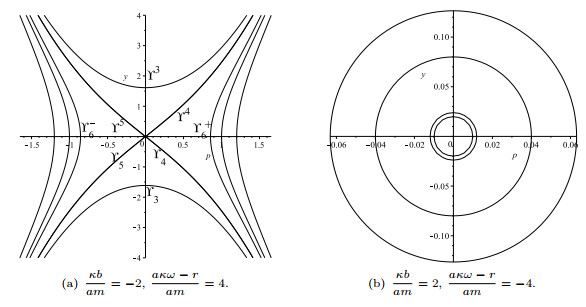
Figure 1. Phase portraits of system (2.3) for
$ \kappa b(a\kappa \omega-r)>0 $ . -
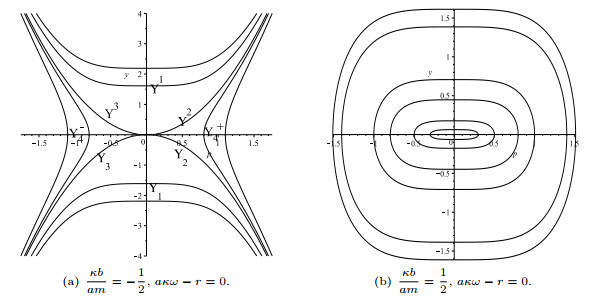
Figure 2. Phase portraits of system (2.3) for
$ \kappa b(a\kappa \omega-r)<0 $ . -
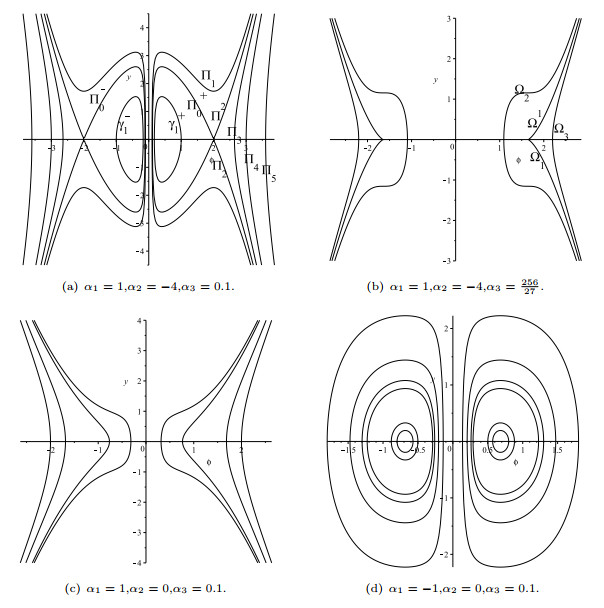
Figure 3. Phase portraits of system (2.3) for
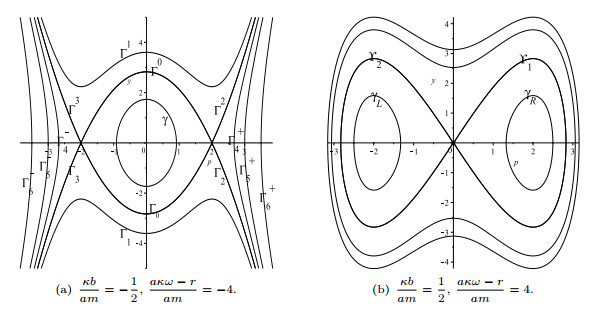
$ a\kappa \omega-r = 0 $ . - Figure 4. Phase portraits of system (2.8).




 DownLoad:
DownLoad: