| Citation: |
M. E. Elbrolosy, A. A. Elmandouh. CONSTRUCTION OF NEW TRAVELING WAVE SOLUTIONS FOR THE (2+1) DIMENSIONAL EXTENDED KADOMTSEV-PETVIASHVILI EQUATION[J]. Journal of Applied Analysis & Computation, 2022, 12(2): 533-550. doi: 10.11948/20210195
|
CONSTRUCTION OF NEW TRAVELING WAVE SOLUTIONS FOR THE (2+1) DIMENSIONAL EXTENDED KADOMTSEV-PETVIASHVILI EQUATION
-
Abstract
This work is interested in constructing traveling wave solutions for the (2+1)-dimensional extended Kadomtsev–Petviashvili equation that is utilized as a model for the surface waves and internal waves in straits or channels. Based on the bifurcation analysis of the traveling wave system, we use the conserved quantity to construct some new bounded traveling wave solutions such as periodic and solitary solutions in addition to some unbounded novel wave solutions. Some of the new solutions and their corresponding orbits are clarified graphically. Moreover, we examine numerically the dynamical behaviour for the perturbed (2+1)-dimensional extended Kadomtsev–Petviashvili equation by adding a perturbed periodic term.
-
-
References
[1] I. Ahmed, A. R. Seadawy and D. Lu, Mixed lump-solitons, periodic lump and breather soliton solutions for (2+1)-dimensional extended Kadomtsev-Petviashvili dynamical equation, International Journal of Modern Physics B, 2019, 33(05), 1950019. DOI: 10.1142/S021797921950019X. [2] P. F. Byrd and M. D. Fridman, Handbook of elliptic integrals for engineers and scientists, Berlin: Springer, 1971. [3] S. Beji, Kadomtsev-Petviashvili type equation for entire range of relative water depths, Coastal engineering journal, 2018, 60(1), 60-68. DOI: 10.1080/21664250.2018.1436241. [4] A. Biswas, 1-Soliton solution of the generalized Camassa-Holm Kadomtsev-Petviashvili equation, Communications in Nonlinear Science and Numerical Simulation, 2009, 14(6), 2524-2527. DOI: 10.1016/j.cnsns.2008.09.023. [5] A. H. Bhrawy, M. A. Abdelkawy, S. Kumar and A. Biswas, Solitons and other solutions to Kadomtsev-Petviashvili equation of B-type, Romanian Journal of Physics, 2013, 58(7), 729-748. [6] L. Cheng and Y. Zhang, Multiple wave solutions and auto- Bäcklund transformation for the (3+1)-dimensional generalized B-type Kadomtsev-Petviashvili equation, Computers and Mathematics with Applications, 2015, 70(5), 765-775. DOI: 10.1016/j.camwa.2015.05.028. [7] P. Dubard and V. B. Matveev, Multi-rogue waves solutions: from the NLS to the KP-I equation, Nonlinearity, 2013, 26(12), R93. DOI: 10.1088/0951-7715/26/12/R93. [8] M. Darvishi, M. Najafi, S. Arbabi and L. Kavitha, Exact propagating multi-anti-kink soliton solutions of a (3+1)-dimensional B-type Kadomtsev-Petviashvili equation, Nonlinear Dynamics, 2016, 83(3), 1453-1462. DOI: 10.1007/s11071-015-2417-2. [9] G. Ebadi, N. Y. Fard, H. Triki and A. Biswas, Exact solutions of the (2+1)-dimensional Camassa-Holm Kadomtsev-Petviashvili equation, Nonlinear Analysis: Modelling and Control, 2012, 17(3), 280-296. doi: 10.15388/NA.17.3.14056 [10] G. Ebadi, A. H. Kara, M. D. Petkovic, A. Yildirim and A. Biswas, Solitons and conserved quantities of the Ito equation, Proceedings of the Romanian Academy: Series A, 2012, 13, 215-224. [11] G. Ebadi, N. Y. Fard, A. H. Bhrawy, S. Kumar, H. Triki, A. Yildirim and A. Biswas, Solitons and other solutions to the (3+1)-dimensional extended Kadomtsev-Petviashvili equation with power law nonlinearity, Romanian Reports in Physics, 2013, 65, 27-62. [12] K. El-Rashidy, A. R. Seadawy, S. Althobaiti and M. M. Makhlouf, Multiwave, Kinky breathers and multi-peak soliton solutions for the nonlinear Hirota dynamical system, Results in Physics, 2020, 19, 103678. DOI: 10.1016/j.rinp.2020.103678. [13] K. El-Rashidy, New traveling wave solutions for the higher Sharma-Tasso-Olver equation by using extension exponential rational function method, Results in Physics, 2020, 17, 103066. DOI: 10.1016/j.rinp.2020.103066. [14] K. El-Rashidy and A. R. Seadawy, Kinky breathers, multi-peak and multi-wave soliton solutions for the nonlinear propagation of Kundu–Eckhaus dynamical model, International Journal of Modern Physics B, 2020, 34(32), 2050317. DOI: 10.1142/S0217979220503178. [15] K. El-Rashidy, A. R. Seadawy, S. Althobaiti and M. M. Makhlouf, Investigation of interactional phenomena and multi wave solutions of the quantum hydrodynamic Zakharov–Kuznetsov model, Open Physics, 2021, 19(1), 91-99. DOI: 10.1515/phys-2021-0009. [16] A. A. Elmandouh and A. G. Ibrahim, Bifurcation and travelling wave solutions for a (2+1)-dimensional KdV equation, Journal of Taibah University for Science, 2020, 14 (1), 139-147. DOI: 10.1080/16583655.2019.1709271. [17] A. A. Elmandouh, Bifurcation and new traveling wave solutions for the 2D Ginzburg–Landau equation, European Phyical Journal Plus, 2020, 135, 648. DOI: 10.1140/epjp/s13360-020-00675-3. [18] M. E. Elbrolosy and A. A. Elmandouh, Bifurcation and new traveling wave solutions for (2+1)-dimensional nonlinear Nizhnik–Novikov–Veselov dynamical equation, European Phyical Journal Plus, 2020, 135, 533. DOI: 10.1140/epjp/s13360-020-00546-x. [19] M. E. Elbrolosy and A. A. Elmandouh, Dynamical behaviour of nondissipative double dispersive microstrain wave in the microstructured solids, The European Physical Journal Plus, 2021, 136(9), 1-20. DOI: 10.1140/epjp/s13360-021-01957-0. [20] M. E. Elbrolosy, Qualitative analysis and new soliton solutions for the coupled nonlinear Schrödinger type equations, Physica Scripta, 2021. DOI: 10.1088/1402-4896/ac445c. [21] A. A. Elmandouh, Integrability, qualitative analysis and the dynamics of wave solutions for Biswas–Milovic equation, The European Physical Journal Plus, 2021, 136(6), 1-17. DOI: 10.1140/epjp/s13360-021-01626-2. [22] J. Guo, J. He, M. Li and D. Mihalache, Exact solutions with elastic interactions for the (2+1)-dimensional extended Kadomtsev-Petviashvili Equation, Nonlinear Dynamics, 2020, 101, 2413-2422. DOI: 10.1007/s11071-020-05881-3. [23] X. Guan and W. Liu, Multiple-soliton and lump-kink solutions for a generalized (3+1)-dimensional Kadomtsev-Petviashvili equation, Results in Physics, 2020, 17, 103149. DOI: 10.1016/j.rinp.2020.103149. [24] A. J. M. Jawad, Dynamics of shallow water waves with Gardner-Kadomtsev-Petviashvili equation, Discrete and continuous dynamical systems series S, 2015, 8(6), 1155-1164. DOI: 10.3934/dcdss.2015.8.1155. [25] J. Liu and Z. Zeng, Auto- Bäcklund transformation and new exact solutions of the (3+1)-imensional KP equation with variable coefficients, Journal of Theoretical and Applied Physics, 2013, 7, 49. DOI: 10.1186/2251-7235-7-49. [26] J. Li, Y. Zhang and J. Liang, Bifurcation and exact traveling wave solutions for a new integrable non-local equation, Journal of Applied Analysis and Computation, 2021, 11(3), 1588-1599. DOI: 10.11948/20200319. [27] Q. Meng and B. He, Bifurcation analysis and exact traveling wave solutions for a generic two-dimensional sine-Gordon equation in nonlinear optics, Journal of Applied Analysis and Computation, 2020, 10(4), 1443-1463. DOI: 10.11948/20190227. [28] W. Mao, Bifurcation and exact traveling wave solutions of MN-Wang equation, Journal of Applied Analysis and Computation, 2020, 10(1), 210-222. DOI: 10.11948/20190113. [29] W. Ma, Lump solutions to the Kadomtsev-Petviashvili equation, Physics Letters A, 2015, 379(36), 1975-1978. DOI: 10.1016/j.physleta.2015.06.061. [30] S. Manukure, Y. Zhou and W. Ma, Lump solutions to a (2+1)-dimensional extended KP equation, Computers and Mathematics with Applications, 2018, 75(7), 2414-2419. DOI: 10.1016/j.camwa.2017.12.030. [31] M. A. Nuwairan and A. A. Elmandouh, Qualitative analysis and wave propagation of the nonlinear model for low-pass electrical transmission lines, Physica Scripta, 2021, 96(9), 095214. DOI: 10.1088/1402-4896/ac0989. [32] J. Song and J. Li, Bifurcations and exact travelling wave solutions for a shallow water wave model with a non-stationary bottom surface, Journal of Applied Analysis Computation, 2020, 10(1), 350-360. DOI: 10.11948/20190254. [33] A. R. Seadawy and K. El-Rashidy, Dispersive solitary wave solutions of Kadomtsev-Petviashvili and modified Kadomtsev-Petviashvili dynamical equations in unmagnetized dust plasma, Results in Physics 8, 2018, 1216-1222. DOI: 10.1016/j.rinp.2018.01.053. [34] Y. Sun, W. Ma, J. Yu and C. M. Khalique, Dynamics of lump solitary wave of Kadomtsev-Petviashvili-Boussinesq-like equation, Computers and Mathematics with Applications, 2019, 78(3), 840-847. DOI: 10.1016/j.camwa.2019.03.001. [35] A. R. Seadawy, M. Iqbal and D. Lu, Propagation of long-wave with dissipation and dispersion in nonlinear media via generalized Kadomtsive-Petviashvili modified equal width Burgers equation, Indian Journal of Physics, 2020, 94(5), 675-687. DOI: 10.1007/s12648-019-01500-z. [36] H. Triki, S. Crutcher, A. Yildirim, T. Hayat, O. M. Aldossary and A. Biswas, Bright and dark solitons of the modified complex Ginzburg Landau equation with parabolic and dual-power law nonlinearity, Romanian Reports in Physics, 2012, 64, 367-380. [37] H. Triki, A. Yildirim, T. Hayat, O. M. Aldossary and A. Biswas, Topological and non-topological soliton solutions of the bretherton equation, Romanian Reports in Physics, 2012, 64, 672-684. [38] Y. Wang and J. Deng, Explicit solutions and conservation laws of the logarithmic-KP equation, Advances in Difference Equations, Article number 229, 2016, DOI: 10.1186/s13662-016-0948-6. [39] H. Wang, Solitons of the Kadomtsev-Petviashvili equation based on lattice Boltzmann model, Advances in Space Research, 2017, 59(1), 293-301. DOI: 10.1016/j.asr.2016.08.029. [40] A. M. Wazwaz, Multiple-soliton solutions for the KP equation by Hirota's bilinear method and by the tanh-coth method, Applied Mathematics and Computation, 2007, 190(1), 633-640. DOI: 10.1016/j.amc.2007.01.056. [41] A. M. Wazwaz, Two integrable extensions of the Kadomtsev-Petviashvili equation, Central European Journal of Physics, 2011, 91, 49-56. DOI: 10.2478/s11534-010-0056-2. [42] A. M. Wazwa, Extended KP equations and extended system of KP equations: multiple-soliton solutions, Canadian Journal of Physics, 2011, 89(7), 739-743. DOI: 10.1139/p11-065. [43] A. M. Wazwaz, Gaussian solitary waves for the logarithmic-KdV and the logarithmic-KP equations, Physica Scripta, 2014, 89(9), 095206. DOI: 10.1088/0031-8949/89/9/095206. [44] S. Xie, L. Wang and Y. Zhang, Explicit and implicit solutions of a generalized Camassa-Holm Kadomtsev-Petviashvili equation, Communications in Nonlinear Science and Numerical Simulation, 2012, 17(3), 1130-1141. DOI: 10.1016/j.cnsns.2011.07.003. [45] Z. Xu, H. Chen, M. Jiang, M. Dai and W. Chen, Resonance and deflection of multi-soliton to the (2+1)-dimensional Kadomtsev-Petviashvili equation, Nonlinear Dynamics, 2014, 78, 461-466, DOI: 10.1007/s11071-014-1452-8. [46] J. Yu and Y. Sun, Study of lump solutions to dimensionally reduced generalized KP equations, Nonlinear Dynamics, 2017, 87, 2755-2763. DOI: 10.1007/s11071-016-3225-z. [47] J. Zhuang and Y. Zhou, Bifurcation and exact traveling wave solutions of the equivalent complex short-plus equations, Journal of Applied Analysis Computation, 2020, 10(2), 795-815. DOI: 10.11948/20190408. -
-
Figures(10) / Tables(1)
Export File
Citation
M. E. Elbrolosy, A. A. Elmandouh. CONSTRUCTION OF NEW TRAVELING WAVE SOLUTIONS FOR THE (2+1) DIMENSIONAL EXTENDED KADOMTSEV-PETVIASHVILI EQUATION[J]. Journal of Applied Analysis & Computation, 2022, 12(2): 533-550. doi: 10.11948/20210195
Format
Content
DownLoad:
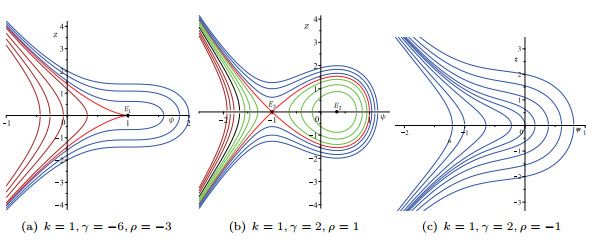
- Figure 1. Phase portrait for the planar dynamical system (2.5). The solid circles indicate to the equilibrium points.
-
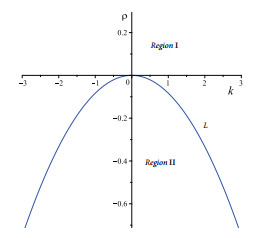
Figure 2. Bifurcation boundary on the
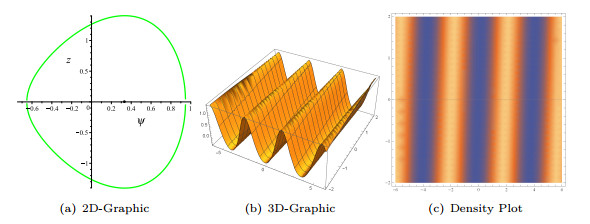
$ k\rho $ -plane for a fixed value of$ \gamma $ . - Figure 3. Graphic representations for the periodic solution (3.5).
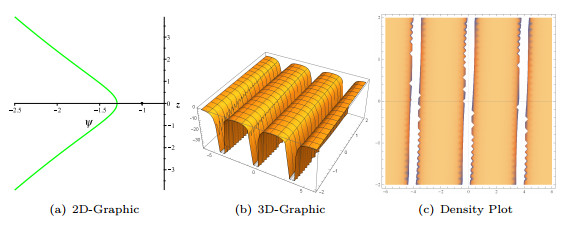
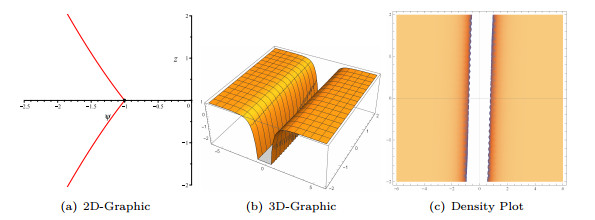
- Figure 4. Graphic representations for the solution (3.14).
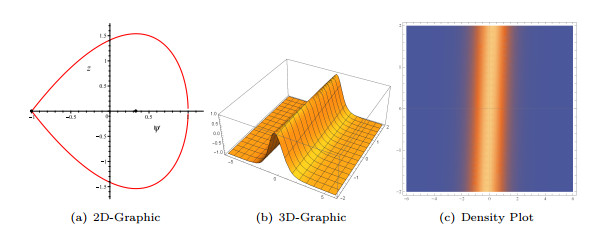
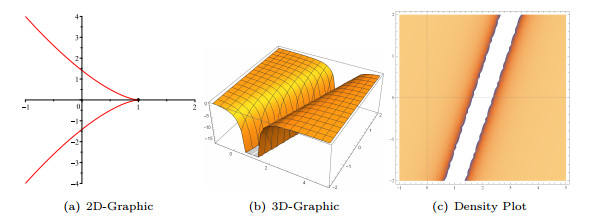
- Figure 5. Graphic representations for the solitary solution (3.7).
- Figure 6. Graphic representations for the solution (3.17).
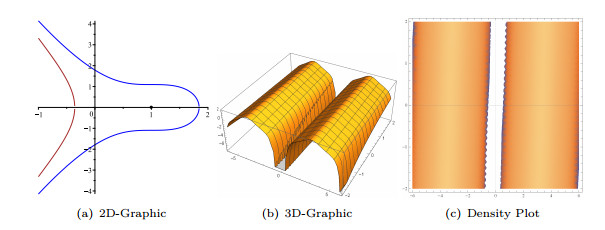
- Figure 7. Graphic representations for the solution (3.10).
- Figure 8. Graphic representations for the solution (3.9).
-
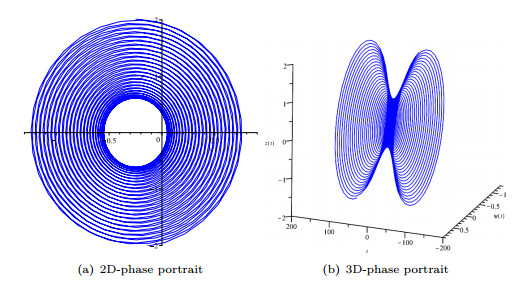
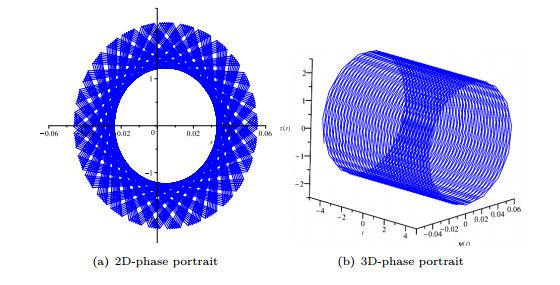
Figure 9. Phase portrait for the dynamical system (5.3) when
$ k=1, p=-0.05, q=2, \rho=-1, \gamma=1 $ , and$ \psi(0)=0.05, z(0)=0.05 $ . -
Figure 10. Phase portrait for the dynamical system (5.3) when
$ k=0.04, p=5, q=0.05, \rho=4, \gamma=2 $ , and$ \psi(0)=0.05, z(0)=1 $ .