| Citation: |
Mohamed Ch-Chaoui, Karima Mokni. ASYMPTOTIC ANALYSIS OF AN INTEGRO-DIFFERENTIAL SYSTEM MODELING THE BLOW UP OF CANCER CELLS UNDER THE IMMUNE RESPONSE[J]. Journal of Applied Analysis & Computation, 2022, 12(5): 1763-1785. doi: 10.11948/20210296
|
ASYMPTOTIC ANALYSIS OF AN INTEGRO-DIFFERENTIAL SYSTEM MODELING THE BLOW UP OF CANCER CELLS UNDER THE IMMUNE RESPONSE
-
Abstract
In this paper, we derive and analyze a phenomenological model at the cellular level of the immune response to cancer evolution based on the kinetic theory of active particles. The model consists of a system of nonlinear integro-differential equations describing the binary interactions between epithelial, tumor, naive immune cells, and activated immune cells. It also takes into account the phenotypic mutations in the epithelial and immune cells, which are known to result in the uncontrolled growth of tumor cells. We prove the well-posedness of the related Cauchy problem and the non-negativity of the solution. We give sufficient conditions for which the solution may exist globally in time. A detailed asymptotic analysis has been developed with the aim of predicting the effect of mutation events on the tumor-immune dynamics. The analysis shows that under some critical values of the model's parameters and initial conditions, we can specify some biological states of the blow up of tumor cells. Indeed, the analysis gives useful indications to be properly explored toward the design of therapeutical actions.
-
-
References
[1] A. K. Abbas and A. H. Lichtman, Basic Immunology. In: Functions and Disorders of the Immune System, Elsevier, Philadelphia, 2004. [2] J. A. Adam and N. Bellomo, A survey of models for tumor-immune system dynamics, Springer Science & Business Media, 2012. [3] B. Allen and M. Nowak, Games on Graphs, Eur. Math. Soc. Surveys in Math. Sci., 2014, 1, 113–151. doi: 10.4171/EMSS/3 [4] P. M. Altrock, L. Liu and F. Michor, The Mathematics Of Cancer: Integrating Quantitative Models, Nature Review Cancer, 2015, 12, 15, 730-745. [5] L. Afraites, A. Atlas, A. Bellouquid and M. Ch-Chaoui, Modelling the complex immune system response to cancer cells, Mathematics in Engineering, Science and Aerospace, 2012, 3(3), 269-283. [6] L. Arlotti, E. De Angelis, L. Fermo, M. Lachowicz and N. Bellomo, On a class of integro-differential equations modeling complex systems with nonlinear interactions, Appl. Math. Letters, 2012, 25, 490-495. doi: 10.1016/j.aml.2011.09.043 [7] B. Aylaj, Qualitative analysis and simulation of a nonlinear integro-differential system modeling tumor-immune cells competition, International Journal of Biomathematics, 2018, 11(08), 1850104. DOI: https://doi.org/10.1142/S1793524518501048. [8] N. Bellomo, A. Elaiw, A. M. Althiabi and M. A. Alghamdi, Mathematics toward systems biology and complexity, Physics of Life Reviews, 2015, 12, 85-90. doi: 10.1016/j.plrev.2015.02.006 [9] N. Bellomo, L. Preziosi and G. Forni, A kinetic (cellular) theory for competition between tumors and the host immune system, J. Biol. Sys., 1996, 4, 497-502. [10] A. Bellouquid and M. Delitala, Mathematical Modeling of Complex Biological Systems. A Kinetic Theory Approach, Birkäuser, Boston, 2006. [11] N. Bellomo, A. Bellouquid and M. Delitala, Mathematical Topics on the Modelling Complex Multicellular Systems and Tumor Immune Cells Competition, Mathematical Models and Methods in Applied Sciences, 2004, 14, 1683-1733. doi: 10.1142/S0218202504003799 [12] N. Bellomo and M. Delitala, From the mathematical kinetic, and stochastic game theory to modelling mutations, onset, progression and immune competition of cancer cells, Physics of Life Reviews, 2008, 5, 183-206. doi: 10.1016/j.plrev.2008.07.001 [13] N. Bellomo, Nonlinear models and problems in applied sciences from differential quadrature to generalized collocation methods, Math. Comp. Modelling, 1997, 26, 13-34. [14] A. Bellouquid and M. CH-Chaoui, Asymptotic analysis of a nonlinear integro-differential system modeling the immune response, Comput. Math. Appl., 2014, 68, 905-914. DOI: https://doi.org/10.1016/j.camwa.2014.05.018. [15] C. Bianca and M. Delitala, On the modelling of genetic mutations and immune system competition, Comput. Math. Appl., 2011, 61, 2362-2375. doi: 10.1016/j.camwa.2011.01.024 [16] A. Bellouquid, E. De Angelis and D. Knopoff, From the modeling of the immune hallmarks of cancer to a black swan in biology, Math. Models Methods Appl. Sci., 2013, 23 949-978. doi: 10.1142/S0218202512500650 [17] B. Cal, B. Molon and A. Viola, Tuning cancer fate: the unremitting role of host immunity, Open Biology, 2017, 7(4), 170006. doi: 10.1098/rsob.170006 [18] F. Cavallo, C. De Giovanni, P. Nanni, G. Forni and P. L. Lollini, 2011: the immune hallmarks of cancer, Cancer Immunol. Immunother, 2011, 60, 319-326. doi: 10.1007/s00262-010-0968-0 [19] E. L. Cooper, Evolution of immune system from self/not self to danger to artificial immune system, Physics of Life Reviews, 2010, 7, 55-78. doi: 10.1016/j.plrev.2009.12.001 [20] M. Ch-Chaoui, A. Eladdadi and K. Mokni, Activation of the immune response by cytokines and its effect on tumour cells: a mathematical model, Letters in Biomathematics, 2018, 5, 1-23. DOI: DOI:10.1080/23737867.2018.1468725. [21] J. Deguine et al., Intravital imaging reveals distinct dynamics for natural killer and $CD8^{+} $ T cells during tumor regression, Immunity, 2010, 33, 632. doi: 10.1016/j.immuni.2010.09.016 CrossRef $CD8^{+} $ T cells during tumor regression" target="_blank">Google Scholar
[22] E. De Angelis, On the Mathematical Theory of Post-Darwinian Mutations, Selection, and Evolution, Mathematical Models and Methods in Applied Sciences, 2014, 24(13), 2723-2742. DOI: https://doi.org/10.1142/S0218202514500353. [23] R. Eftimie and G. Eftimie, Tumour-associated macrophages and oncolytic virotherapies: a mathematical investigation into a complex dynamics, Letters in Biomathematics, 2018, 5(2), S6-S35. DOI: https://doi.org/10.1080/23737867.2018.1430518. [24] A. Eladdadi, L. de Pillis and K. Peter, Modelling tumour-immune Dynamics, Disease Progression and Treatment, Letters in Biomathematics, 2018, 5(2), S1-S5. DOI: https://doi.org/10.1080/23737867.2018.1483003. [25] R. Eftimie, J. J Gillard and D. A Cantrell, Mathematical Models for Immunology: Current State of the Art and Future Research Directions, Bull. Math. Biol., 2016, 78, 2091-2134. doi: 10.1007/s11538-016-0214-9 [26] O. J. Finn, Immuno-oncology: understanding the function and dysfunction of the immune system in cancer, Annals of Oncology, 2012, 23, 6-9. [27] H. Gintis, Game Theory Evolving: A Problem-Centered Introduction to Modeling Strategic Interaction, Princeton University Press, 2009. [28] F. G. Giancotti, Deregulation of cell signaling in cancer, FEBS Letters, 2014, 588(16), 2558-2570. doi: 10.1016/j.febslet.2014.02.005 [29] D. Hanahan and L. M. Coussens, Accessories to the crime: functions of cells recruited to the tumor microenvironment, Cancer Cell, 2012, 21(3), 309-322. doi: 10.1016/j.ccr.2012.02.022 [30] B. Jeremy Swann and M. J. Smyth, Immune surveillance of tumors, J. Clin. Invest., 2007, 117(5), 1137-1146. doi: 10.1172/JCI31405 [31] R. Kim, K. Emi and K. Tanabe, Cancer immunoediting from immune surveillance to immune escape, Immunology, 2007, 121(1), 1-14. doi: 10.1111/j.1365-2567.2007.02587.x [32] N. Kedia-Mehta and D. K Finlay, Competition for nutrients and its role in controlling immune responses, Nat. Commun., 2019, 10, 2123. doi: 10.1038/s41467-019-10015-4 [33] J. Liu and X. Cao, Cellular and molecular regulation of innate inflammatory responses, Cell Mol. Immunol., 2016, 13, 711-721. doi: 10.1038/cmi.2016.58 [34] K. J. Mahasa, R. Ouifki, A. Eladdadi and L. de Pillis, A combination therapy of oncolytic viruses and chimeric antigen receptor T cells: a mathematical model proof-of-concept, Mathematical Biosciences and Engineering, 2022, 19(5), 4429-4457. doi: 10.3934/mbe.2022205 [35] A. Niida, K. Mimori, T. Shibata et al., Modeling colorectal cancer evolution, J. Hum. Genet., 2021, 66, 869-878. DOI: https://doi.org/10.1038/s10038-021-00930-0. [36] E. Piretto, M. Delitala and M. Ferraro, Efficiency of cancer treatments: in silico experiments, Math. Model. Nat. Phenom., 2020, 15-19. DOI: https://doi.org/10.1051/mmnp/2019031. [37] R. D. Schreiber, R. J. Old Lloyed and J. Smyth Mark, Cancer Immunoediting: Integrating Immunity's Roles in Cancer Suppression and Promotion, Science, 2011, 331, 1565. doi: 10.1126/science.1203486 [38] N. S. Senekal, K. J. Mahasa, A. Eladdadi et al., Natural Killer Cells Recruitment in Oncolytic Virotherapy: A Mathematical Model, Bull. Math. Biol., 2021, 83, 75. DOI: https://doi.org/10.1007/s11538-021-00903-6. [39] A. Shabir, U. Aman, A. Ali and B. Dumitru, Theoretical and numerical analysis of fractal fractional model of tumor-immune interaction with two different kernels, Alexandria Engineering Journal, 2022, 61(7), 5735-5752. DOI: https://doi.org/10.1016/j.aej.2021.10.065. [40] A. Shabir, U. Aman, A. Thabet, A. Ali and M. Nabil, Analysis of fractal-fractional model of tumor-immune interaction, Results in Physics, 2021, 25, 104178. DOI: https://doi.org/10.1016/j.rinp.2021.104178. [41] A. Schmidt, N. Oberle and P. H. Krammer, Molecular mechanisms of treg-mediated T cell suppression, Front. Immunol., 2012, 2012(3), 51. [42] R. A. Weinberg, The Biology of Cancer, Garland Sciences-Taylor and Francis, 2007. [43] J. A. Wargo, S. M. Reddy, A. Reuben and P. Sharma, Monitoring immune responses in the tumor microenvironment, Current opinion in immunology, 2016, 41, 23-31. [44] T. L. Whiteside, Immune responses to malignancies, The Journal of allergy and clinical immunology, 2010, 125(2), S272-S283. [45] B. F. Zamarron and W. Chen, Dual Roles of Immune Cells and Their Factors in Cancer Development and Progression, International Journal of Biological Scienc, 2011, 7(5), 651-658. -
-
Figures(5) / Tables(1)
Export File
Citation
Mohamed Ch-Chaoui, Karima Mokni. ASYMPTOTIC ANALYSIS OF AN INTEGRO-DIFFERENTIAL SYSTEM MODELING THE BLOW UP OF CANCER CELLS UNDER THE IMMUNE RESPONSE[J]. Journal of Applied Analysis & Computation, 2022, 12(5): 1763-1785. doi: 10.11948/20210296
Format
Content
DownLoad:
-
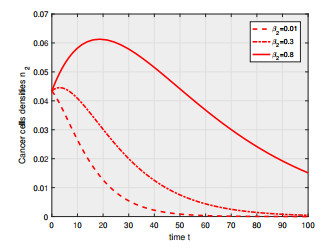
Figure 1. Numerical simulation of the model showing the evolution of the number density of cancer cells versus time for different value of their proliferation rate. The mutation events are absent, that is,
$ \varepsilon_1=0 $ and$ \varepsilon_2 = 0 $ -
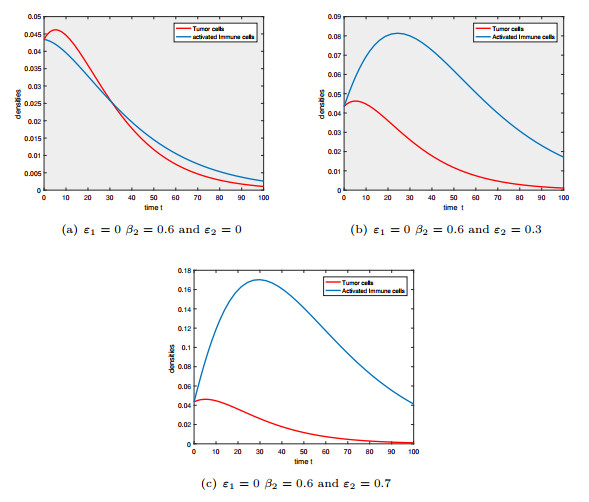
Figure 2. Numerical simulation of the model (2.9)-(2.10) showing the evolution the evolution of tumor cells (
$ n_2 $ ) and activated immune cells ($ n_4 $ ) versus time$ t $ . -
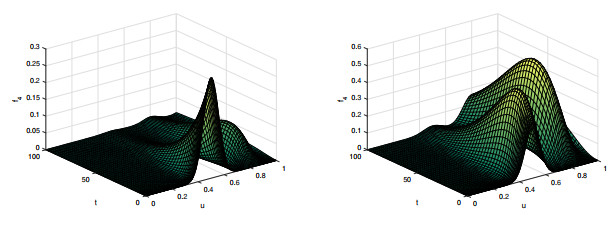
Figure 3. Numerical simulation of the model (2.9)-(2.10) showing the evolution of the distribution functions
$ f_2(t,u) $ for$ \varepsilon_2=0 $ (left panel) and$ \varepsilon_2=0.6 $ (right panel). These two figures are performed with an intermediate value of$ \beta_2=0.2 $ and$ \varepsilon_1=0 $ -
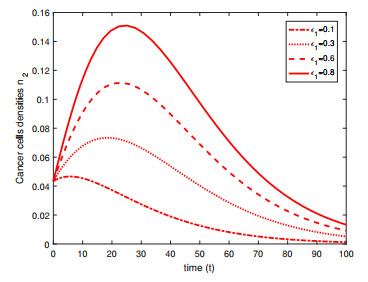
Figure 4. Numerical simulation of the model (2.9)-(2.10) showing the evolution of
$ n_2 $ versus time, for different values of$ \varepsilon_1 $ . The mutation events in activated immune cells are absents$ \varepsilon_2=0 $ -
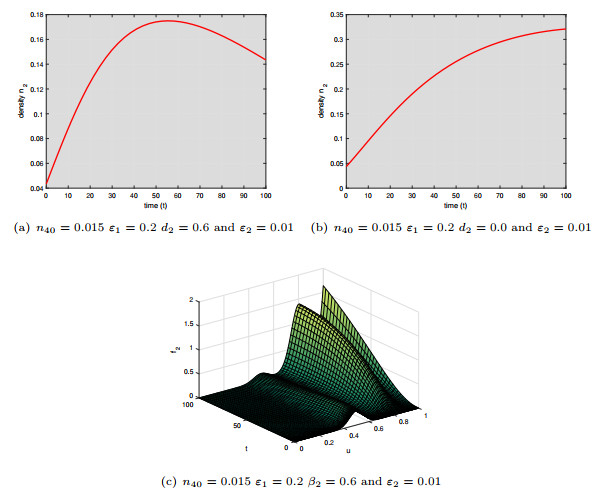
Figure 5. Numerical simulation of the model (2.9)-(2.10) showing the evolution the evolution of tumor cells (
$ n_2 $ ) versus time$ t $ in the case$ \varepsilon_2 <\varepsilon_2^*=0.03 $ et$ n_{40}< n_{40}^{*}=0.1 $