| Citation: | Qiuyan Zhang. BIFURCATIONS AND EXACT SOLUTIONS OF THE OPTICAL SOLITON MODEL IN METAMATERIALS DOMINATED BY ANTI-CUBIC NONLINEARITY[J]. Journal of Applied Analysis & Computation, 2022, 12(4): 1517-1531. doi: 10.11948/20210317 |
BIFURCATIONS AND EXACT SOLUTIONS OF THE OPTICAL SOLITON MODEL IN METAMATERIALS DOMINATED BY ANTI-CUBIC NONLINEARITY
-
Abstract
Optical soliton model in metamaterials, dominanted by anti-cubic nonlinearity, is investigated by the method of dynamical systems. By using travelling wave transformation, the model can be converted into a singular integrable travelling wave system. Then we discuss the dynamical behavior of the associated regular system. Further, all bounded exact solutions of the model can be calculated because of its integrability. Finally, twenty exact explicit parametric representations are derived.
-
Keywords:
- Bifurcation /
- homoclinic orbit /
- heteroclinic orbit /
- periodic peakon /
- optical soliton model
-

-
References
[1] S. S. Afzal, M. Younis and S. T. R. Rizvi, Optical dark and dark-singular solitons with anti-cubic nonlinearity, Optik, 2017, 147, 27–31. doi: 10.1016/j.ijleo.2017.08.067 [2] K. S. Al-Ghafri1 and E. V. Krishnan, Optical solitons in metamaterials dominated by anti-cubic nonlinearity and Hamiltonian perturbations, Int. J. Appl. Comput. Math., 2020, 6(5), 144. doi: 10.1007/s40819-020-00896-1 [3] A. H. Arnous, M. Ekici, S. P. Moshokoa et al, Solitons in nonlinear directional couplers with optical metamaterials by trial function scheme, Acta Phys. Polonica A., 2017, 132(4), 1399–1410. doi: 10.12693/APhysPolA.132.1399 [4] A. Biswas, R. Kaisar, K. R. Khan et al, Bright and dark solitons in optical metamaterials, Optik, 125(13), 3299–3302. [5] A. Biswas, A. Mirzazadeh, M. Savescu et al, Singular solitons in optical metamaterials by ansatz method and simplest equation approach, J. of Modern Optics, 2014, 61(19), 1550–1555. doi: 10.1080/09500340.2014.944357 [6] P. F. Byrd and M. D. Fridman, Handbook of Elliptic Integrals for Engineers and Sciensists, Springer, Berlin, 1971. [7] M. Ekici, A. Sonmezoglu, Q. Zhou et al, Analysis of optical solitons in nonlinear negative-indexed materials with anti-cubic nonlinearity, Opt. Quantum Electron., 2018, 50(2), 75. doi: 10.1007/s11082-018-1341-3 [8] M. Foroutan, J. Manafian and A. Ranjbaran, Solitons in optical metamaterials with anti-cubic law of nonlinearity by generalized GG' -expansion method, Optik, 2018, 162, 86–94. doi: 10.1016/j.ijleo.2018.02.087 [9] M. Foroutan, J. Manafian and I. Zamanpour, Solitonwave solutions in optical metamaterials with anti-cubic law of nonlinearity by ITEM, Optik, 2018, 164, 371–379. doi: 10.1016/j.ijleo.2018.03.025 [10] Y. Fu and J. Li, Exact stationary-wave solutions in the standard model of the Kerr-nonlinear optical fiber with the bragg grating, J. Appl. Anal, Comput., 2017, 7(3), 1177–1184. [11] A. A. Kader, M. A. Latif and Q. Zhou, Exact optical solitons in metamaterials with anti-cubic law of nonlinearity by Lie group method, Opt. Quantum Electron, 2019, 51(1), 30. doi: 10.1007/s11082-019-1748-5 [12] J. Li, Geometric properties and exact travelling wave solutions for the generalized Burger-Fisher equation and the Sharma-Tasso-Olver equation, J. Nonl. Mod. Anal., 2019, 1(1), 1–10. [13] J. Li, Singular Nonlinear Traveling Wave Equations: Bifurcations and Exact Solutions, Science Press, Beijing, 2013. [14] J. Li and G. Chen, Bifurcations of travelling wave solutions for four classes of nonlinear wave equations, Int. J. Bifurcat. Chaos, 2005, 15(12), 3973–3998. doi: 10.1142/S0218127405014416 [15] J. Li and G. Chen, On a class of singular nonlinear traveling wave equations, Int. J. Bifurcat. Chaos, 2007, 17(11), 4049–4065. doi: 10.1142/S0218127407019858 [16] J. Li and M. Han, Exact peakon solutions given by the generalized hyperbolic functions for some nonlinear wave equations, J. Appl. Anal, Comput., 2020, 10(4), 1708–1719. [17] J. Li, Y. Zhang and X. Zhao, On a class of singular nonlinear traveling wave equations (Ⅱ): an example of GCKdV equations, Int. J. Bifurcat. Chaos, 2009, 19(6), 1955–2007. [18] J. Li, W. Zhou, and G. Chen, Understanding peakons, periodic peakons and compactons via a shallow water wave equation, Int. J. Bifurcat. Chaos, 2016, 26(12), 1650207. doi: 10.1142/S0218127416502072 [19] A. Sonmezoglu, M. Yao, M. Ekici et al, Explicit solitons in the parabolic law nonlinear negative-index materials, Nonlinear Dynam., 2016, 88(1), 1–13. [20] Y. Xiang, X. Dai, S. Wen et al, Controllable Raman soliton self-frequency shift in nonlinear metamaterials, Phys. Rev. A, 2011, 84(3), 2484–2494. [21] Y. Xu, P. Pablo Suarez, D. Milovic et al, Raman solitons in nanoscale optical waveguides, with metamaterials, having polynomial law non-linearity, J. Mod. Optic., 2016, 63(S3), S32–S37. [22] Y. Zhou and J. Li, Exact solutions and dynamics of the Raman soliton model in nanoscale optical waveguides, with metamaterials, having polynomial law nonlinearity, Int. J. Bifurcat. Chaos, 2017, 27(12), 1750188. doi: 10.1142/S0218127417501887 [23] Q. Zhou, L. Liu, Y. Liu et al, Exact optical solitons in metamaterials with cubicšCquintic nonlinearity and third-order dispersion, Nonlinear Dynam., 2015, 80(3), 1365–1371. doi: 10.1007/s11071-015-1948-x [24] Q. Zhou, M. Mirzazadeh, M. Ekici et al, Analytical study of solitons in non-Kerr nonlinear negative index materials, Nonlinear Dynam., 2015, 86(1), 623–638. [25] Y. Zhou and J. Zhuang, Bifurcations and exact eolutions of the Raman soliton model in nanoscale optical waveguides with metamaterials, J. Nonl. Mod. Anal., 2021, 3(1), 145–165. -
-
-
Figure 1. The bifurcations of phase portraits of system (1.7) as
$ b_1 $ is varied. -
Figure 2. The level curves
$ H_1(\phi,y)=h $ of system (1.7) as$ h $ is varied for$ h_3<h_1<h_2 $ -
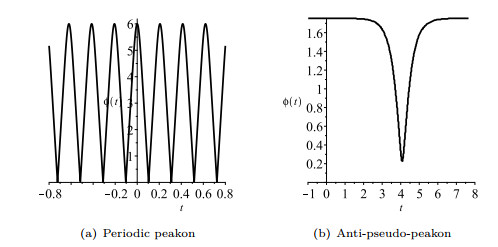
Figure 3. The profiles of the solution
$ \phi(\xi) $ of system (1.7) -
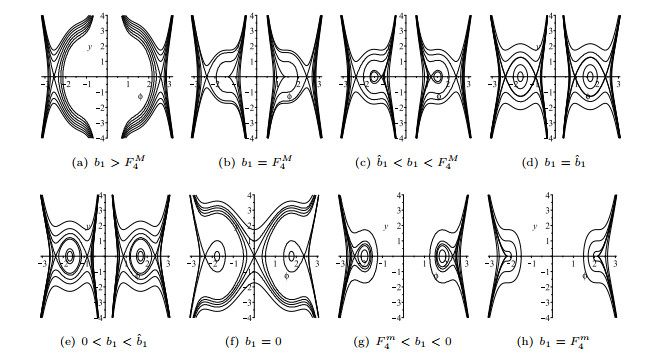
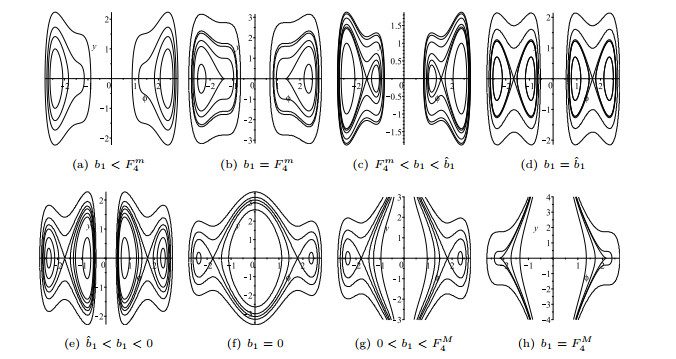
Figure 4. The bifurcations of phase portraits of system (1.7) as
$ b_1 $ is varied. -
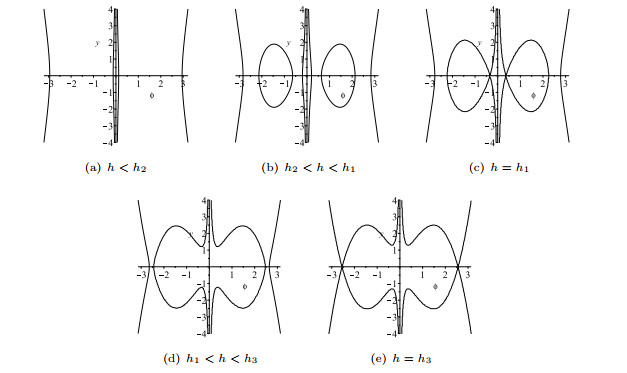
Figure 5. The level curves
$ H_1(\phi,y)=h $ of system (1.7) as$ h $ is varied for$ h_2<h_1<h_3 $ -
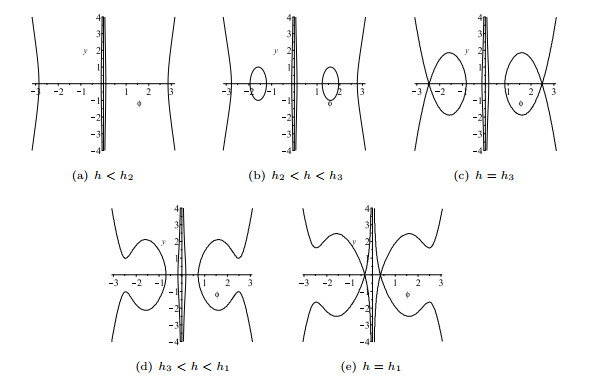
Figure 6. The level curves defined by
$ H_1(\phi,y)=h $ of system (1.7) as$ h $ is varied for$ h_2<h_3<h_1 $ .




 DownLoad:
DownLoad: