| Citation: | Xuqing Zhang, Yidu Yang, Hai Bi. STABILIZED TWO-GRID DISCRETIZATIONS OF LOCKING FREE FOR THE ELASTICITY EIGENVALUE PROBLEM[J]. Journal of Applied Analysis & Computation, 2024, 14(4): 1831-1853. doi: 10.11948/20220048 |
STABILIZED TWO-GRID DISCRETIZATIONS OF LOCKING FREE FOR THE ELASTICITY EIGENVALUE PROBLEM
-
Abstract
In this paper, we propose two stabilized two-grid finite element discretizations for nearly incompressible elasticity eigenvalue problem and give the error estimates of eigenvalues and eigenfunctions for the schemes. Numerical experiments are provided to validate our theoretical analysis and exhibit that our schemes are locking free and highly efficient.
-

-
References
[1] A. Andreev, R. Lazarov and M. Racheva, Postprocessing and higher order convergence of the mixed finite element approximations of biharmonic eigenvalue problems, Am. J. Comput. Appl. Math., 2005, 182, 333-349. doi: 10.1016/j.cam.2004.12.015 [2] D. Arnold, J. Douglas and C. Gupta, A family of higher order mixed finite element methods for plane elasticity, Numer. Math., 1984, 45, 1222. [3] I. Babuška and J. Osborn, Eigenvalue Problems, in: P. G. Ciarlet, J. L. Lions (Eds. ), Finite Element Methods (Part 1), Handbook of Numerical Analysis, vol. 2, Elsevier Science Publishers, North-Holand, 1991. [4] I. Babuška and M. Suri, Locking effects in the finite element approximation of elasticity problems, Numer. Math., 1992, 62, 439-463. doi: 10.1007/BF01396238 [5] I. Babuška and M. Suri, On locking and robustness in the finite element method, SIAM J. Numer. Anal., 1992, 29, 1261-1293. doi: 10.1137/0729075 [6] F. Bertrand, D. Boffi and R. Ma, An adaptive finite element scheme for the hellinger-reissner elasticity mixed eigenvalue problem, Comput. Methods Appl. Math., 2021, 21(3), 501-512. doi: 10.1515/cmam-2020-0034 [7] H. Bi, X. Zhang and Y. Yang, The nonconforming crouzeix-raviart element approximations and two-grid discretizations for the elastic eigenvalue problem, J. Comput. Math., 2023, 41(6), 1041-1063. doi: 10.4208/jcm.2201-m2020-0128 [8] D. Boffi, Finite element approximation of eigenvalue problems, Acta Numer., 2010, 19, 1-120. doi: 10.1017/S0962492910000012 [9] S. Brenner, Poincaré-friedrichs inequalities for piecewise $h^1$ functions, SIAM J. Numer. Anal., 2003, 41, 306-324. doi: 10.1137/S0036142902401311 [10] S. Brenner and L. Scoot, The Mathematical Theory of Finite Element Methods, 3rd ed., Springer, New York, 2010. [11] S. Brenner and L. Sung, Linear finite element methods for planar linear elasticity, Math. Comp., 1992, 59(200), 321-338, . doi: 10.1090/S0025-5718-1992-1140646-2 [12] J. Chen, Y. Xu and J. Zou, An adaptive inverse iteration for maxwell eigenvalue problem based on edge elements, J. Comput. Phys., 2010, 229, 2649-2658. doi: 10.1016/j.jcp.2009.12.013 [13] L. Chen, Ifem: An Innovative Finite Element Methods Package in Matlab. Technical Report, University of California at Irvine, 2009. [14] M. Crouzeix and P. Raviart, Conforming and nonconforming finite element methods for solving the stationary stokes equations, RAIRO Anal. Numer., 1973, 3, 33-75. [15] X. Dai and A. Zhou, Three-scale finite element discretizations for quantum eigenvalue problems, SIAM J. Numer. Anal., 2008, 46, 295-324. doi: 10.1137/06067780X [16] B. Gong, J. Han, J. Sun and Z. Zhang, A shifted-inverse adaptive multigrid method for the elastic eigenvalue problem, Commun. Comput. Phys., 2019, 27(1), 251-273. [17] J. Han, Z. Zhang and Y. Yang, A new adaptive mixed finite element method based on residual type a posterior error estimates for the stokes eigenvalue problem, Numer. Methods Partial Differ. Equ., 2015, 31(1), 31-53. doi: 10.1002/num.21891 [18] P. Hansbo and M. Larson, Discontinuous galerkin and the crouzeix-raviart element: Application to elasticity, M2AN Math. Model Numer. Anal., 2003, 37(1), 63-72. doi: 10.1051/m2an:2003020 [19] X. Hu and X. Cheng, Corrigendum to: Acceleration of a two-grid method for eigenvalue problems, Math. Comput., 2015, 84, 2701-2704. doi: 10.1090/mcom/2967 [20] X. Huang and J. Huang, The compact discontinuous galerkin method for nearly incompressible linear elasticity, J. Sci. Comput., 2013, 56, 291-318. doi: 10.1007/s10915-012-9676-6 [21] D. Inzunza, F. Lepe and G. Rivera, Displacement-pseudostress formulation for the linear elasticity spectral problem, Numer. Methods Partial Differential Eq., 2023, 39, 1996-2017. doi: 10.1002/num.22955 [22] K. Kim, Analysis of some low-order nonconforming mixed finite elements for linear elasticity problem, Numer. Methods Partial Differ. Equ., 2006, 22, 638-660. doi: 10.1002/num.20114 [23] J. Lee and H. Kim, Analysis of a staggered discontinuous galerkin method for linear elasticity, J. Sci. Comput., 2016, 66, 625-649. doi: 10.1007/s10915-015-0036-1 [24] M. Li, D. Shi and Z. Li, The stabilized mixed finite element scheme of elasticity problem, Comput. Appl. Math., 2017, 37(3), 2588-2604. [25] S. Meddahi, D. Mora and R. Rodr$\acute{i}$guez, Finite element spectral analysis for the mixed formulation of the elasticity equations, SIAM J. Numer. Anal., 2013, 51(2), 1041-1063. doi: 10.1137/120863010 [26] M. Morley, A family of mixed finite elements for linear elasticity, Numer. Math., 1989, 55, 633-666. doi: 10.1007/BF01389334 [27] A. Russo, Eigenvalue approximation by mixed non-conforming finite element methods, Calcolo, 2014, 51(4), 563-597. doi: 10.1007/s10092-013-0101-9 [28] M. Vogelius, An analysis of the p-version of the finite element method for nearly incompressible materials. uniformly valid, optimal order estimates, Numer. Math., 1983, 41, 39-53. doi: 10.1007/BF01396304 [29] F. Wang, S. Wu and J. Xu, A mixed discontinuous galerkin method for linear elasticity with strongly imposed symmetry, J. Sci. Comput., 2020, 83(2), 1-17. [30] J. Xu and A. Zhou, A two-grid discretization scheme for eigenvalue problems, Math. Comput., 1999, 70(233), 17-26. doi: 10.1090/S0025-5718-99-01180-1 [31] J. Xu and A. Zhou, Two-grid discretization scheme for eigenvalue problems, Math. Comput., 2001, 70, 17-25. [32] Y. Yang and H. Bi, A two-grid discretization scheme based on the shifted-inverse power method, SIAM J. Numer. Anal., 2011, 49(4), 1602-1624. doi: 10.1137/100810241 [33] Y. Yang, H. Bi, J. Han and Y. Yu, The shifted-inverse iteration based on the multigrid discretizations for eigenvalue problems, SIAM J. Sci. Comput., 2015, 37(6), A2583-A2606. doi: 10.1137/140992011 [34] Y. Yang and Z. Chen, The order-preserving convergence for spectral approximation of self-adjoint completely continuous operators, Sci. China Ser. A, 2008, 51, 1232-1242. [35] B. Zhang and J. Zhao, A mixed formulation of stabilized nonconforming finite element method for linear elasticity, Adv. Appl. Math. Mech., 2020, 12(1), 278-300. doi: 10.4208/aamm.OA-2019-0048 [36] X. Zhang, Y. Yang and Y. Zhang, A locking-free shifted inverse iteration based on multigrid discretization for the elastic eigenvalue problem, Math. Methods Appli. Sci., 2021, 44(7), 5821-5838. doi: 10.1002/mma.7150 [37] Y. Zhang, H. Bi and Y. Yang, The two-grid discretization of ciarlet-raviart mixed method for biharmonic eigenvalue problems, Appl. Numer. Math., 2019, 138, 94-113. doi: 10.1016/j.apnum.2018.12.007 [38] J. Zhou, X. Hu, L. Zhong, et al., Two-grid methods for maxwell eigenvalue problems, SIAM J. Numer. Anal., 2014, 52, 2027-2047. doi: 10.1137/130919921 -
-
-
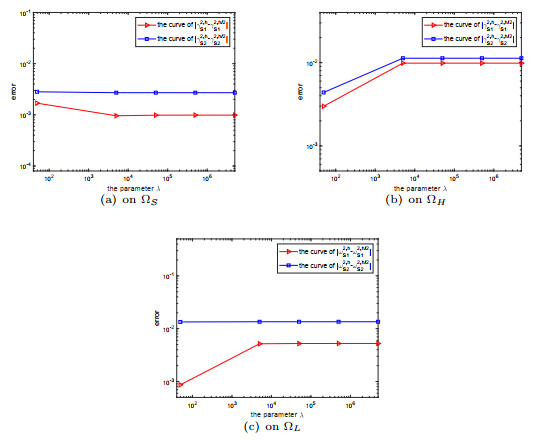
Figure 1.
Error curves of the first eigenvalue.
-
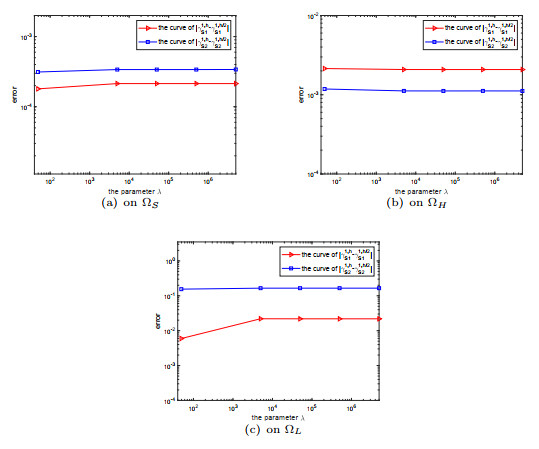
Figure 2.
Error curves of the second eigenvalue.




 DownLoad:
DownLoad: