| Citation: |
Ping Yang, Yiping Lin. STABILITY SWITCHING CURVES AND HOPF BIFURCATION ON A THREE SPECIES FOOD CHAIN WITH TWO DELAYS[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 1062-1076. doi: 10.11948/20220118
|
STABILITY SWITCHING CURVES AND HOPF BIFURCATION ON A THREE SPECIES FOOD CHAIN WITH TWO DELAYS
-
Abstract
A three species food chain with two time delays and double Holling type-Ⅱ functional responses is investigated. The conditions for the existence of positive equilibrium and Hopf bifurcation are presented. The stability area of positive equilibrium is surrounded by coordinate axis and stability switching curves. By using the theory of Hassard, Hopf bifurcation directions are determined analytically. Numerical simulations are presented on the frontier of stability to explain and support the analytic results.
-
-
References
[1] A. A. Arafa, Y. Xu and G. M. Mahmoud, Chaos suppression via integrative time delay control, Int. J. Bifurcat. Chaos, 2020. DOI: 10.1142/S0218127420502089. [2] K. L. Cooke and Z. Grossman, Discrete delay, distributed delay and stability switches, J. Math. Anal. Appl., 1982, 86, 592-627. doi: 10.1016/0022-247X(82)90243-8 [3] G. Cui and X. Yan, Stability and bifurcation analysis on a three-species food chain system with two delays, Commun. Nonlinear Sci. Numer. Simulat., 2011, 16, 3704-3720. doi: 10.1016/j.cnsns.2010.12.042 [4] J. Fan and Y. Lin, Bifurcation and chaos of a three species food chain system with time delay, 2011 Fourth International Workshop on Chaos-Fractals Theories and Applications, 2011. DOI: 10.1109/IWCFTA.2011.41. [5] S. Gakkhar and A. Singh, Control of chaos due to additional predator in the Hastings-Powell food chain model, J. Math. Anal. Appl., 2012, 385, 423-438. doi: 10.1016/j.jmaa.2011.06.047 [6] A. A. Gomes, E. Manica and M. C. Varriale, Applications of chaos control techniques to a three-species food chain, Chaos Solit. Fract., 2008, 36, 1097-1107. doi: 10.1016/j.chaos.2006.07.027 [7] K. Gu, S. I. Niculescu and J. Chen, On stability crossing curves for general systems with two delays, J. Math. Anal. Appl., 2005, 311, 231-253. doi: 10.1016/j.jmaa.2005.02.034 [8] J. K. Hale and W. Huang, Global geometry of the stable regions for two delay differential equations, J. Math. Anal. Appl., 1993, 178, 344-362. doi: 10.1006/jmaa.1993.1312 [9] B. Hassard, D. Kazarinoff and Y. Wan, Theory and Applications of Hopf Bifurcation, Cambridge University Press, Cambridge, 1981. [10] A. Hastings and T. Powell, Chaos in three species food chain, Ecology, 1991, 72, 896-903. doi: 10.2307/1940591 [11] X. Lin and H. Wang, Stability analysis of delay differential equations with two discrete delays, Can. Appl. Math. Q., 2012, 20, 519-533. [12] K. E. Lonngren, E. Bai and A. Ucar, Dynamics and synchronization of the Hastings-Powell model of the food chain, Chaos Solit. Fract., 2004, 20, 387-393. doi: 10.1016/S0960-0779(03)00421-1 [13] S. Lv and M. Zhao, The dynamic complexity of a three species food chain model, Chaos Solit. Fract., 2008, 37, 1469-1480. doi: 10.1016/j.chaos.2006.10.057 [14] A. Matsumotoa and F. Szidarovszky, Stability switching curves in a Lotka-Volterra competition system with two delays, Math. and Comput. Simulat., 2020, 178, 422-438. doi: 10.1016/j.matcom.2020.06.017 [15] O. P. Misra and A. R. Babu, Modelling effect of toxicant in a three-species food-chain system incorporating delay in toxicant uptake process by prey, Model. Earth Syst. Environ., 2016. DOI: 10.1007/s40808-016-0128-4. [16] O. Moaaz and A. Muhib, New oscillation criteria for nonlinear delay differential equations of fourth-order, Appl. Math. Comput., 2020. DOI: 10.1016/j.amc.2020.125192. [17] H. A. E. Morshedy and A. R. Herrera, Criteria of global attraction in systems of delay differential equations with mixed monotonicity, J. Differ. Equations, 2020, 268, 5945-5968. doi: 10.1016/j.jde.2019.11.016 [18] R. D. Parshad, R. K. Upadhyay, S. Mishra, S. K. Tiwari and S. Sharma, On the explosive instability in a three-species food chain model with modified Holling type Ⅳ functional response, Math. Method. Appl. Sci., 2017, 40, 5707-5726. doi: 10.1002/mma.4419 [19] K. A. Pawelek, S. Liu, F. Pahlevani and L. Rong, A model of HIV-1 infection with two time delays: Mathematical analysis and comparison with patient data, Math. Biosci., 2012, 235, 98-109. doi: 10.1016/j.mbs.2011.11.002 [20] H. Qiu and W. Deng, Optimal harvesting of a stochastic delay tri-trophic food-chain model with Levy jumps, Physica A: Statistical Mechanics and its Applications, 2018, 492, 1715-1728. doi: 10.1016/j.physa.2017.11.092 [21] H. Su and J. Xu, Time-delayed sampled-data feedback control of differential systems undergoing Hopf bifurcation, Int. J. Bifurcat. Chaos, 2021. DOI: 10.1142/S0218127421500048. [22] C. Tian and L. Zhang, Hopf bifurcation analysis in a diffusive food-chain model with time delay, Comput. Math. Appl., 2013, 66, 2139-2153. doi: 10.1016/j.camwa.2013.09.002 [23] M. C. Varriale and A. A. Gomes, A study of a three species food chain, Ecol. Model., 1998, 110, 119-133. doi: 10.1016/S0304-3800(98)00062-3 [24] F. Wang, S. Zhang and L. Chen, Permanence and complexity of a three species food chain with impulsive effect on the top predator, Int. J. Nonlinear Sci. Numer. Simul., 2005, 6, 169-180. [25] R. Xu, L. Chen and F. Hao, Periodic solutions of a discrete time Lotka-Volterra type food-chain model with delays, Appl. Math. Comput., 2005, 171, 91-103. doi: 10.1016/j.amc.2005.01.027 [26] P. Yang, J. Fang, Y. Dai and Y. Lin, Rank-one chaos in a periodically kicked three-species food chain with time-delay, Int. J. Bifurcat. Chaos, 2020. DOI: 10.1142/S0218127420500388. [27] Z. Zhang, S. Kundub, J. P. Tripathi and S. Bugalia, Stability and Hopf bifurcation analysis of an SVEIR epidemic model with vaccination and multiple time delays, Chaos Solit. Fract., 2020. DOI: 10.1016/j.chaos.2019.109483. -
-
Figures(5)
Export File
Citation
Ping Yang, Yiping Lin. STABILITY SWITCHING CURVES AND HOPF BIFURCATION ON A THREE SPECIES FOOD CHAIN WITH TWO DELAYS[J]. Journal of Applied Analysis & Computation, 2022, 12(3): 1062-1076. doi: 10.11948/20220118
Format
Content
DownLoad:
-
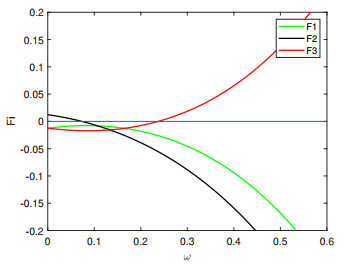
Figure 1. For
$ a_1=5, b_1=2, d_1=0.6, a_2=0.2, b_2=0.3, d_2=0.02, $ $ F1, F2, F3 $ are all less then$ 0 $ if$ \omega \in (0.0738, 0.2371) $ . -
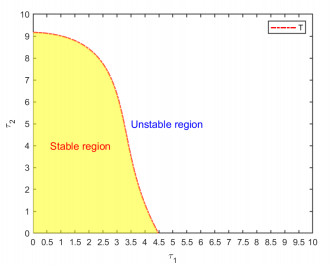
Figure 2. For
$ a_1=5, b_1=2, d_1=0.6, a_2=0.2, b_2=0.3, d_2=0.02, $ $ \mathit{T} $ is a switching curve on$ \tau_1-\tau_2 $ plane with$ \omega \in (0.0738, 0.2371) $ .$ E_* $ is stable in the region surrounded by$ \tau_1=0, \tau_2=0 $ and curve$ T $ . -
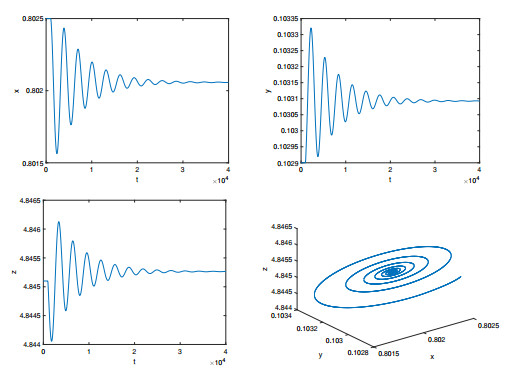
Figure 3. When
$ \tau_1=2.91, \tau_2=3.44, $ $ E_* $ is asymptotically stable. -
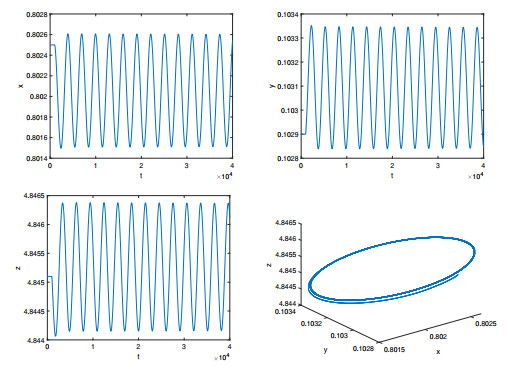
Figure 4. When
$ \tau_1=3.51, \tau_2=3.44, $ $ E_* $ is unstable, and there is a stable periodic solution surrounding$ E_* $ . -
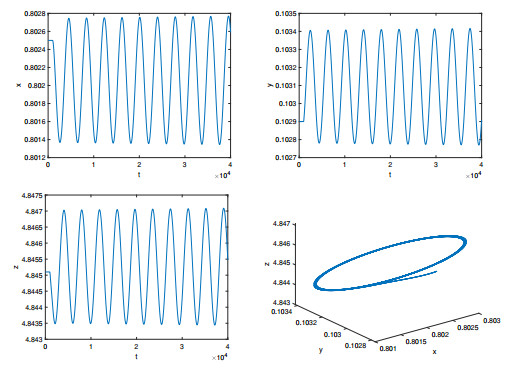
Figure 5. When
$ \tau_1=2.91, \tau_2=6.68, $ $ E_* $ is unstable and there is a stable periodic solution surrounding$ E_* $ .