| Citation: |
Parvin Kumari, Devendra Kumar, Higinio Ramos. PARAMETER INDEPENDENT SCHEME FOR SINGULARLY PERTURBED PROBLEMS INCLUDING A BOUNDARY TURNING POINT OF MULTIPLICITY ≥ 1[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1304-1320. doi: 10.11948/20220123
|
PARAMETER INDEPENDENT SCHEME FOR SINGULARLY PERTURBED PROBLEMS INCLUDING A BOUNDARY TURNING POINT OF MULTIPLICITY ≥ 1
-
Abstract
A numerical scheme is developed for parabolic singularly perturbed boundary value problems, including multiple boundary turning points at the left endpoint of the spatial direction. The highest order derivative of these problems is multiplied by a small parameter $ \varepsilon\, (0< \varepsilon\ll 1) $, and when it is close to zero, the solution exhibits a parabolic type boundary layer near the left lateral surface of the domain of consideration. Thus, large oscillations appear when classical/standard numerical methods are used to solve the problem, and one cannot achieve the expected accuracy. Thus, the Crank-Nicolson scheme on a uniform mesh in the temporal direction and an upwind scheme on a Shishkin-type mesh in the spatial direction is constructed. The theoretical analysis shows that the method converges irrespective of the size of $ \varepsilon $ with accuracy $ \mathcal{O}((\Delta t)^2+N^{-1}\ln N) $. Three test examples are presented to verify that the computational results agree with the theoretical ones.
-
-
References
[1] L. Bobisud, Second-order linear parabolic equations with a small parameter, Arch. Rational Mech. Anal., 1968, 27, 385-397. doi: 10.1007/BF00251441 [2] R. K. Dunne, E. O'Riordan and G. I. Shishkin, A fitted mesh method for a class of singularly perturbed parabolic problems with a boundary turning point, Comput. Methods Appl. Math., 2003, 3, 361-372. doi: 10.2478/cmam-2003-0023 [3] P. A. Farrell, A. F. Hegarty, J. J. H. Miller, E. O'Riordan and G. I. Shishkin, Robust Computational Techniques for Boundary Layers, Chapman & Hall, London, 2000. [4] V. Gupta and M. K. Kadalbajoo, A layer adaptive B-spline collocation method for singularly perturbed one-dimensional parabolic problem with a boundary turning point, Numer. Methods Part. Diff. Eqn., 2011, 27, 1143-1164. doi: 10.1002/num.20574 [5] T. C. Hanks, Model relating heat-flow values near, and vertical velocities of mass transport beneath, oceanic rises, J. Geophys Res., 1971, 76, 537-544. doi: 10.1029/JB076i002p00537 [6] R. B. Kellogg and A. Tsan, Analysis of some difference approximations for a singular perturbation problem without turning point, Math. Comp., 1978, 32, 1025-1039. doi: 10.1090/S0025-5718-1978-0483484-9 [7] D. Kumar and P. Kumari, A parameter-uniform numerical scheme for the parabolic singularly perturbed initial boundary value problems with large time delay, J. Appl. Math. Comput., 2019, 159, 79-206. [8] O. A. Ladyzhenskaya, V. A. Solonnikov and N. N. Ural'tseva, Linear and Quasilinear Equations of Parabolic Type, Translations of Mathematical Monographs, Vol. 23, American Mathematical Society, USA, 1968. [9] T. Lin and R. Vulanović, Uniform methods for semi linear problems with an attractive boundary turning point, Novi Sad J. Math., 2001, 31, 99-114. [10] V. D. Liseikin and V. E. Petrenko, Adaptive-Invariant Method for Numerical Solution of Problems with Boundary and Internal Layers, Novosibirsk, 1989. [11] V. D. Liseikin, The use of special transformations in the numerical solution of boundary layer problems, USSR Comput. Math. Math. Phys., 1990, 30, 43-53. doi: 10.1016/0041-5553(90)90006-E [12] J. J. H. Miller, E. O'Riordan and G. I. Shishkin, Fitted Numerical Methods for Singular Perturbation Problems, World Scientific, Singapore, 1996. [13] P. Rai and K. K. Sharma, Singularly perturbed parabolic differential equations with turning point and retarded arguments, J. Appl. Math., 2015, 45, 4. [14] H. G. Roos, M. Stynes and L. Tobiska, Numerical Methods for Singular Perturbed Differential Equations, Springer-Verlag, New York, 1996. [15] A. A. Samarskii, Theory of Finite-Difference Approximations, Moscow, 1989. [16] H. Schlichting, Boundary Layer Theory, McGraw-Hill, New York, 1979. [17] G. I. Shishkin, Grid approximations to singularly perturbed parabolic equations with turning points, Differ. Equn., 2001, 37, 1037-1050. doi: 10.1023/A:1011978225750 [18] R. Vulanović, On numerical solution of a mildly nonlinear turning point problem, Math. Model. Num. Anal., 1990, 24, 765-783. doi: 10.1051/m2an/1990240607651 [19] R. Vulanović and P. Lin, Numerical solution of quasi linear attractive turning point problems, Comput. Math. Appl., 1992, 23, 75-82. [20] R. Vulanović and P. A. Farrell, Continuous and numerical analysis of a multiple turning point problem, SIAM J. Numer. Anal., 1993, 30, 1400-1418. doi: 10.1137/0730073 -
-
Figures(5) / Tables(7)
Export File
Citation
Parvin Kumari, Devendra Kumar, Higinio Ramos. PARAMETER INDEPENDENT SCHEME FOR SINGULARLY PERTURBED PROBLEMS INCLUDING A BOUNDARY TURNING POINT OF MULTIPLICITY ≥ 1[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1304-1320. doi: 10.11948/20220123
Format
Content
DownLoad:
-
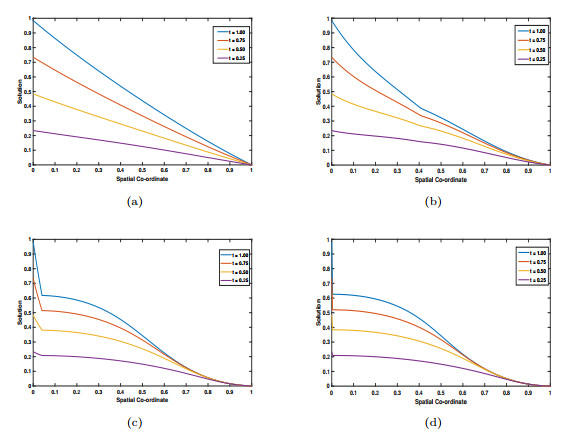
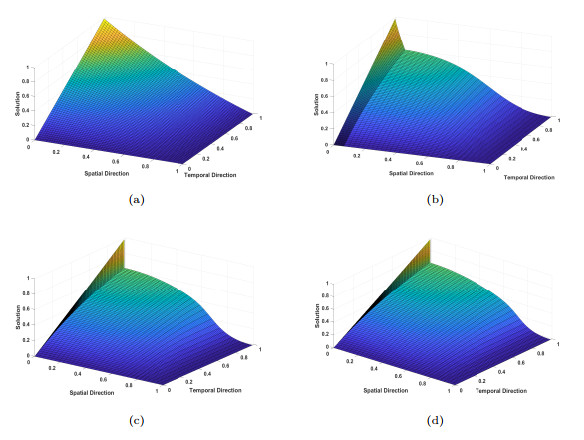
Figure 1.
Numerical solution profiles for Example 5.1 for (a)
$ \varepsilon=1, p = 1 $ $ \varepsilon=2^{-6}, p = 3 $ $ \varepsilon=2^{-12}, p = 5 $ $ \varepsilon=2^{-18}, p = 7 $ -
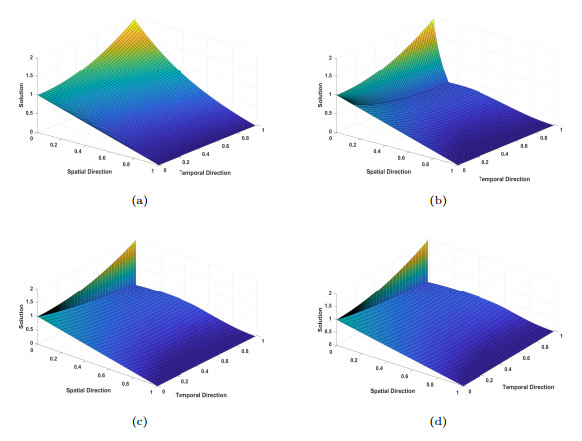
Figure 2.
Numerical solution profiles for
$ p=2 $ $ \varepsilon=1 $ $ \varepsilon=0.1 $ $ \varepsilon=0.01 $ $ \varepsilon=0.001 $ -
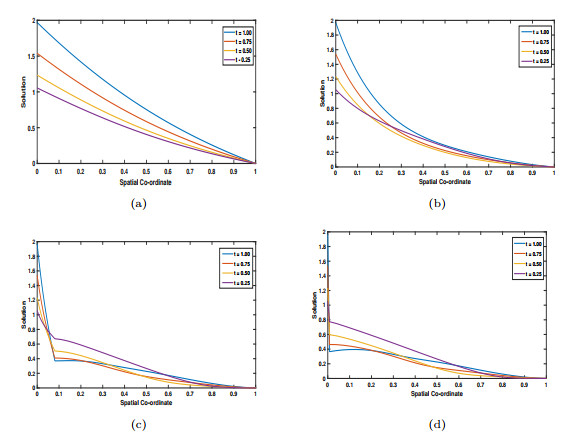
Figure 3.
Numerical solution profiles for Example 5.2 for (a)
$ \varepsilon=1, p = 1 $ $ \varepsilon=2^{-6}, p = 3 $ $ \varepsilon=2^{-12}, p = 5 $ $ \varepsilon=2^{-18}, p = 7 $ -
Figure 4.
Numerical solution profiles for
$ p=2 $ $ \varepsilon=1 $ $ \varepsilon=0.1 $ $ \varepsilon=0.01 $ $ \varepsilon=0.001 $ -
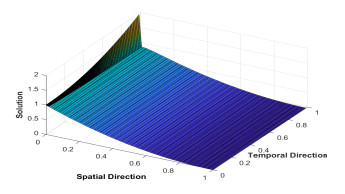
Figure 5.
Surface plots of the numerical solution for Example 5.3 for
$ \varepsilon=2^{-8}, p = 1 $