| Citation: |
Dan Jin, Ruizhi Yang. HOPF BIFURCATION IN A PREDATOR-PREY MODEL WITH MEMORY EFFECT AND INTRA-SPECIES COMPETITION IN PREDATOR[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1321-1335. doi: 10.11948/20220127
|
HOPF BIFURCATION IN A PREDATOR-PREY MODEL WITH MEMORY EFFECT AND INTRA-SPECIES COMPETITION IN PREDATOR
-
Abstract
This paper investigates the spatiotemporal dynamics of a reaction diffusion predator-prey model that incorporates memory delay and intra-species competition in predator. We provide rigorous results of the model including the local stability of positive equilibrium, the existence and the property of Hopf bifurcation. We show that increasing the intra-species competition is not beneficial to the stability of the positive equilibrium. Moreover, we obtain that the stable region of the positive equilibrium will decrease with the increase of memory-based diffusion coefficient when it larger than the critical value. In addition, the memory delay may also affect the stability of the positive equilibrium. When the memory delay crosses the critical value, the stable positive equilibrium becomes unstable, and the stably inhomogeneous periodic solutions appears. These results indicate that the memory delay and intra-species competition play an important role in the spatiotemporal dynamics of predator-prey model.
-
-
References
[1] B. Abrahms, E. L. Hazen, E. O. Aikens, et al., Memory and resource tracking drive blue whale migrations, Proceedings of the National Academy of Sciences, 2019, 116(12), 5582-5587. doi: 10.1073/pnas.1819031116 [2] Q. An, C. Wang and H. Wang, Analysis of a spatial memory model with nonlocal maturation delay and hostile boundary condition, Discrete & Continuous Dynamical Systems, 2020, 40, 5845-5868. [3] X. Cao and W. Jiang, Turing-Hopf bifurcation and spatiotemporal patterns in a diffusive predator-prey system with Crowley-Martin functional response, Nonlinear Analysis: Real World Applications, 2018, 43, 428-450. doi: 10.1016/j.nonrwa.2018.03.010 [4] P. H. Crowley and E. K. Martin, Functional responses and interference within and between year classes of a dragonfly population, Journal of the North American Benthological Society, 1989, 8(3), 211-221. doi: 10.2307/1467324 [5] W. F. Fagan, Migrating whales depend on memory to exploit reliable resources, Proceedings of the National Academy of Sciences, 2019, 116(12), 5217-5219. doi: 10.1073/pnas.1901803116 [6] W. F. Fagan and M. A. Lewis, M. Auger-Méthé, et al., Spatial memory and animal movement, Ecology Letters, 2014, 16(10), 1316-1329. [7] Z. Fang, S. Chen and J. Wei, Global dynamics of a diffusive Leslie-Gower predator-prey model with fear effect, Journal of Nonlinear Modeling and Analysis, 2022, 4(1), 129-140. [8] Y. Guo and S. Sun, Asymptotic Behavior of a Stochastic Predator-prey Model with Beddington-DeAngelis Functional Response and Lévy jumps, Journal of Nonlinear Modeling and Analysis, 2022, 4(4), 764-782. [9] X. Hou, J. Fu and H. Cheng, sensitivity analysis of pesticde dose on predator-prey system with a prey refuge, Journal of Applied Analysis & Computation, 2022, 12(1), 270-293. [10] D. Hu, Y. Zhang, Z. Zheng, et al., Dynamics of a delayed predator-prey model with constant-yield prey harvesting, Journal of Applied Analysis & Computation, 2022, 12(1), 302-335. [11] C. Liu, S. Li and Y. Yan, Hopf bifurcation analysis of a density predator-prey model with Crowley-Martin functional response and two time delays, Journal of Applied Analysis & Computation, 2019, 9(4), 1589-1605. [12] C. Lu, X. Ding and L. Zhang, Stationary distributton and permanence of a stochastic delay predator-prey Lotka-Volterra with Lévy jumps, Journal of Applied Analysis & Computation, 2022, 12(4), 1328-1352. [13] P. R. Moorcroft, M. A. Lewis and R. L. Crabtree, Home range analysis using amechanistic home range model, Ecology, 1999, 80(5), 1656-1665. doi: 10.1890/0012-9658(1999)080[1656:HRAUAM]2.0.CO;2 [14] J. R. Potts and M. A. Lewis, Spatial memory and taxis-driven pattern formation in model ecosystems, Bulletin of Mathematical Biology, 2019, 81(7), 2725-2747. doi: 10.1007/s11538-019-00626-9 [15] J. P. Tripathi, S. Bugalia, V. Tiwari, et al., A predator-prey model with Crowley-Martin functional response: A nonautonomous study, Natural Resource Modeling, 2020, 33(4), e12287. [16] J. P. Tripathi, S. Tyagi and S. Abbas, Global analysis of a delayed density dependent predator-prey model with Crowley-Martin functional response, Communications in Nonlinear Science and Numerical Simulation, 2016, 30(1-3), 45-69. doi: 10.1016/j.cnsns.2015.06.008 [17] S. Xu, M. Qu and C. Zhang, Investigating the Turing conditions for diffusion-driven instability in predator-prey system with hunting cooperation functional response, Journal of Nonlinear Modeling and Analysis, 2021, 3(4), 663-676. [18] C. Xu and Y. Yu, Stability analysis of time delayed fractional order predator-prey system with Crowley-Martin functional response, Journal of Applied Analysis & Computation, 2019, 9(3), 928-942. [19] Q. Shi, J. Shi and H. Wang, Spatial movement with distributed delay, Journal of Mathematical Biology, 2021, 82, 33. doi: 10.1007/s00285-021-01588-0 [20] J. Shi, C. Wang and H. Wang, Diffusive spatial movement with memory and maturation delays, Nonlinearity, 2019, 32(9), 3188-3208. doi: 10.1088/1361-6544/ab1f2f [21] J. Shi, C. Wang, H. Wang, et al., Diffusive spatial movement with memory, Journal of Dynamics and Differential Equations, 2020, 32, 979-1002. doi: 10.1007/s10884-019-09757-y [22] Y. Song, Y. Peng and T. Zhang, The spatially inhomogeneous Hopf bifurcation induced by memory delay in a memory-based diffusion system, Journal of Differential Equations, 2021, 300, 597-624. [23] Y. Song, S. Wu and H. Wang, Spatiotemporal dynamics in the single population model with memory-based diffusion and nonlocal effect, Journal of Differential Equations, 2019, 267, 6316-6351. doi: 10.1016/j.jde.2019.06.025 [24] R. Yang, Bifurcation analysis of a diffusive predator-prey system with Crowley-Martin functional response and delay, Chaos, Solitons & Fractals, 2017, 95, 131-139. [25] R. Yang, D. Jin and W. Wang, A diffusive predator-prey model with generalist predator and time delay, AIMS Mathematics, 2022, 7(3), 4574-4591. doi: 10.3934/math.2022255 [26] R. Yang, C. Nie and D. Jin, Spatiotemporal dynamics induced by nonlocal competition in a diffusive predator-prey system with habitat complexity, Nonlinear Dynamics, 2022, 110(1), 879-900. doi: 10.1007/s11071-022-07625-x [27] R. Yang, Q. Song and Y. An, Spatiotemporal dynamics in a predator-prey model with functional response increasing in both predator and prey densities, Mathematics, 2022, 10(1), 17. [28] R. Yang, F. Wang and D. Jin, Spatially inhomogeneous bifurcating periodic solutions induced by nonlocal competition in a predator-prey system with additional food, Mathematical Methods in the Applied Sciences, 2022, 45, 9967-9978. doi: 10.1002/mma.8349 [29] R. Yang, X. Zhao and Y. An, Dynamical Analysis of a delayed diffusive predator-prey model with additional food provided and anti-predator behavior, Mathematics, 2022, 10, 469. doi: 10.3390/math10030469 -
-
Figures(7)
Export File
Citation
Dan Jin, Ruizhi Yang. HOPF BIFURCATION IN A PREDATOR-PREY MODEL WITH MEMORY EFFECT AND INTRA-SPECIES COMPETITION IN PREDATOR[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1321-1335. doi: 10.11948/20220127
Format
Content
DownLoad:
-
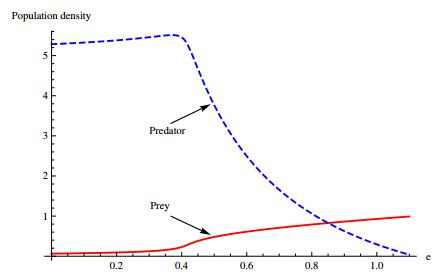
Figure 1.
The population densities of prey and predator with parameter
$ e $ -
Figure 2.
Bifurcation diagram of system
$ (1.2) $ $ e $ $ d=1.5 $ -
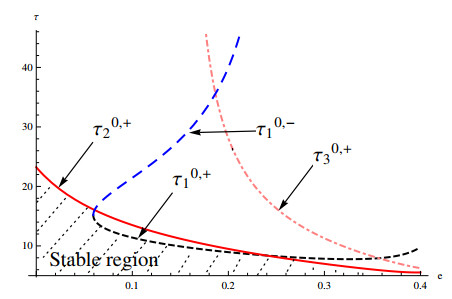
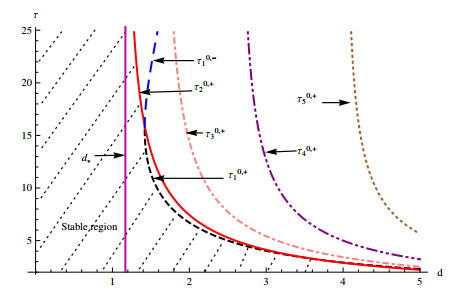
Figure 3.
Bifurcation diagram of system
$ (1.2) $ $ d $ $ e=0.1 $ -
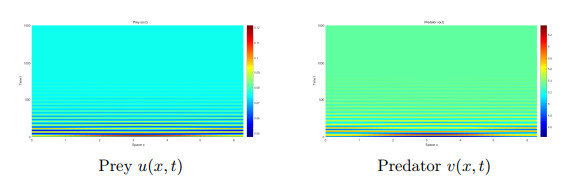
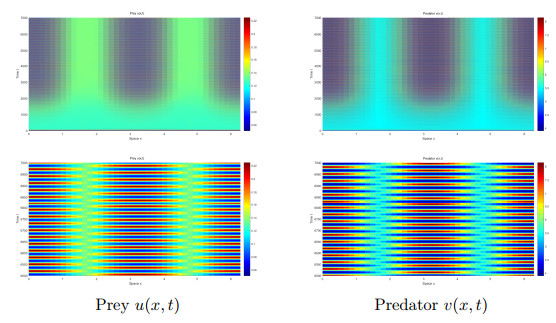
Figure 4.
The numerical simulations of system
$ (1.2) $ $ e=0.1 $ $ \tau=10 $ $ (u_*, v_*) $ -
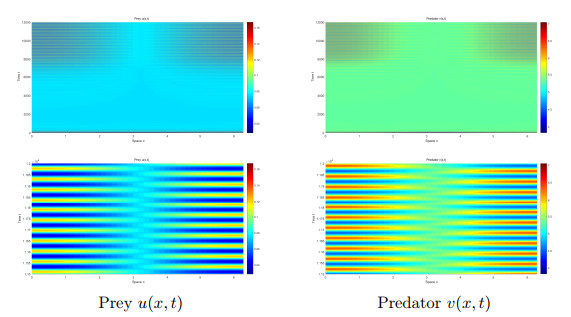
Figure 5.
The numerical simulations of system
$ (1.2) $ $ e=0.1 $ $ \tau=12 $ $ (u_*, v_*) $ -
Figure 6.
The numerical simulations of system
$ (1.2) $ $ e=0.3 $ $ \tau=6.5 $ $ (u_*, v_*) $ -
Figure 7.
The numerical simulations of system
$ (1.2) $ $ e=0.3 $ $ \tau=7.2 $ $ (u_*, v_*) $